المحتويات
ملخص المحتوى
شرح وتبسيط نظرية الألعاب أو نظرية المباريات وتطبيقاتها في مختلف مجالات الحياة الاقتصادية والسياسية والاجتماعية، مع التوضيح بالأمثلة التطبيقية الشيقة والمبسطة.
ما هي نظرية الألعاب
يتطلب الإنتاج والتبادل تعاونًا بين الأفراد على مستوى ما، ولكن التفاعلات نفسها قد تؤدي أيضًا إلى مواجهات كارثية. إن تاريخ البشرية هو تاريخ معارك وحروب بقدر ما هو تاريخ تعاون ناجح. تحمل العديد من التفاعلات البشرية إمكانات التعاون والوئام بالإضافة إلى الصراع والكوارث. والأمثلة على ذلك كثيرة: العلاقات بين الأزواج والأشقاء والبلدان والإدارة ونقابات العمال والجيران والطلاب والأساتذة، وما إلى ذلك.
يمكن للمرء أن يجادل بأن التقنيات والمؤسسات والمعايير الثقافية المعقدة بشكل متزايد والموجودة في المجتمعات البشرية كانت موجودة من أجل تسهيل وتنظيم هذه التفاعلات.
على سبيل المثال، تسهل تكنولوجيا الإنترنت بشكل كبير المعاملات بين المشتري والبائع، ولكنها تعقّدها أيضًا عن طريق زيادة فرص الغش والاحتيال. عادة ما يكون لدى العمال والمديرين مصالح متعارضة عندما يتعلق الأمر بالأجور وظروف العمل، وتوفر النقابات العمالية بالإضافة إلى قانون العمل قنوات وقواعد يمكن من خلالها معالجة أي تضارب محتمل بينهما. وبالمثل، فإن العديد من المعايير الثقافية والدينية، مثل الإيثار أو المعاملة بالمثل، تجلب بعض التنظيم للتفاعلات الخطيرة المحتملة بين الأفراد. كل هذه المعايير والمؤسسات تتطور باستمرار مع تغير طبيعة التفاعلات الأساسية.
وبهذا المعنى، يتطلب فهم السلوك البشري في سياقه الاجتماعي والمؤسسي فهمًا صحيحًا للتفاعل البشري.

نظرية الألعاب ودراسة السلوك البشري
الاقتصاد وعلم الاجتماع وعلم النفس والعلوم السياسية كلها مكرسة لدراسة السلوك البشري في مختلف مجالات الحياة الاجتماعية. ومع ذلك، في كثير من الحالات هي تتعامل مع الأشخاص فرادى، وبعبارة أخرى يفترضون أنه لفهم سلوك فرد ما، فإنه يمكن الثقة بافتراض أن سلوكه ليس له تأثير كبير على الأفراد الآخرين. في بعض الحالات، واعتمادًا على السؤال الذي يطرحه المرء، قد يكون هذا الافتراض مبررًا. على سبيل المثال، ما يقوله مزارع صغير في السوق المحلية في إحدى المدن: “إن رسوم القمح من غير المحتمل أن يكون لها تأثير على أسعار القمح العالمية”. أو ما يمكن أن يقوله شخص يفطن في بلد ما: “إن احتمال أن يغير تصويتي نتيجة الانتخابات الرئاسية ضئيل للغاية”. لذا، إذا كنا مهتمين بالسعر العالمي للقمح أو نتيجة الانتخابات الرئاسية، فقد نفترض بكل ثقة أن فردًا واحدًا يتصرف كما لو أن سلوكه لن يؤثر على النتيجة.
ومع ذلك، في كثير من الحالات، قد يؤدي هذا الافتراض إلى استنتاجات خاطئة. على سبيل المثال، مقدار الرسوم المفروضة على المزارعين في مدينة ما، مقارنة بمدن أخرى، يؤثر بالتأكيد على أسعار المحاصيل في هذه المدينة والمدن الأخرى، إذا حُددت رسوم أقل سيبيع المزارعون المحاصيل بسعر أقل من الأسعار التي حددها المزارعون الآخرون في المدن الأخرى، وبالتالي يبيعون محصولا أكثر من غيرهم، والعكس صحيح.
لذلك، إذا افترضنا أنهم يحددون أسعارهم دون أخذ هذا التأثير في الاعتبار، فمن غير المحتمل أن نقترب من فهم سلوكهم.
وبالمثل، فإن تصويت فرد واحد قد يُغير جذريًا نتيجة التصويت في اللجان الصغيرة، وافتراض أنهم يصوتون مع الجهل بهذه الحقيقة من المرجح أن يكون مضللا.
نظرية الألعاب والتفاعلات الاستراتيجية
موضوع نظرية الألعاب هو بالضبط تلك التفاعلات داخل مجموعة من الأفراد (أو الحكومات والشركات، وما إلى ذلك) حيث يكون لأفعال كل فرد تأثير على النتيجة التي تهم الجميع. ومع ذلك، هذا لا يكفي لأن يكون الموقف موضوعًا صحيحًا لنظرية الألعاب: تدرس نظرية الألعاب التفاعلات الاستراتيجية التي يجب أن تكون تصرفات الأفراد فيها استراتيجية، أي يجب أن يكونوا على دراية بحقيقة أن أفعالهم تؤثر على الآخرين. حقيقة أن أفعالي لها تأثير على النتيجة لا تتطلب سلوكًا استراتيجيًا، إذا لم أكن على علم بهذه الحقيقة. لذلك، فإن نظرية الألعاب تدرس التفاعل الاستراتيجي داخل مجموعة من الأفراد.
والمقصود بالتفاعل الاستراتيجي أن الأفراد يعرفون أن أفعالهم سيكون لها تأثير على النتيجة وتتصرف وفقًا لذلك.
بعد تحديد أنواع المواقف التي تتعامل معها نظرية الألعاب، يجب مناقشة كيفية تحليلها لهذه المواقف.
مثل أي نظرية أخرى، فإن الهدف من نظرية الألعاب هو تنظيم المعرفة وزيادة فهم العالم الخارجي.
تحاول النظرية العلمية تجريد أهم جوانب حالة معينة، وتحليلها باستخدام افتراضات وإجراءات معينة، وفي النهاية اشتقاق بعض المبادئ والتنبؤات العامة التي يمكن تطبيقها على حالات فردية.
لكي تمتلك أي قوة تنبؤية، يجب أن تفترض نظرية الألعاب بعض القواعد التي يتصرف الأفراد وفقًا لها.
إذا لم نصف كيف يتصرف الأفراد، وما هي أهدافهم وكيف هي قواعد اللعبة التي يحاولون اتباعها لتحقيق هذه الأهداف، لا يمكننا اشتقاق أي تنبؤات على الإطلاق في موقف معين. على سبيل المثال، يمكن للمرء الحصول على تنبؤات مختلفة تمامًا فيما يتعلق بسعر القمح في السوق المحلية إذا افترض أن المزارعين ببساطة يستخدمون لعبة رمي قطعة نقدية للاختيار بين البيع بسعر دولار واحد أو دولارين للرطل بحسب ما إذا كانت النتيجة صورة أو كتابة، مقارنة بما يُفترض من أنهم يحاولون كسب أكبر قدر ممكن من المال.
لذلك، لإحضار بعض الانضباط إلى التحليل، يجب على المرء إدخال بعض الهيكلية والتنظيم في قواعد اللعبة.
العقلانية في نظرية الألعاب
إن الافتراض الأهم، وربما أحد أكثر الافتراضات إثارة للجدل، لنظرية الألعاب التي تولد هذا الانضباط هو افتراض أن الأفراد عقلانيون.
الفرد عقلاني إذا كانت لديه أهداف (أو تفضيلات) محددة جيدًا من مجموعة النتائج المحتملة، ويُنفّذ أفضل استراتيجية متاحة لمتابعة هذه الأهداف.
أي أن العقلانية تعني أن الأفراد يعرفون الاستراتيجيات المتاحة لكل فرد، ولديهم تفضيلات كاملة ومتسقة مع النتائج المحتملة، وهم على علم بتلك التفضيلات.
علاوة على ذلك، يمكنهم تحديد أفضل استراتيجية لأنفسهم وتنفيذها بشكل لا تشوبه شائبة.
“إذا تم الأخذ بهذا التعريف حرفيا، فإن افتراض العقلانية هو بالتأكيد أمر غير واقعي، وإذا تم تطبيقه على حالات معينة، فقد ينتج عنه نتائج تتعارض مع الواقع. يجب أن نلاحظ أولا أن مُنظري اللعبة يدركون القيود التي يفرضها هذا الافتراض وهناك مجال بحث نشط يدرس آثار الأشكال الأقل تطلبًا للعقلانية، والتي تسمى العقلانية المحدودة. ومع ذلك، في هذا الموضوع لن يتم التطرق لهذا المجال من البحث. علاوة على ذلك، لتقدير المشاكل مع افتراض العقلانية، يجب على المرء أولا أن يرى نتائجها. لذلك، بدون الخوض في الكثير من المناقشة، سوف نقول جدلا بأنه يجب على المرء أن يعامل العقلانية كحالة مقيدة. سيكون لديك فرصة كافية في هذا الكتاب لتقرر بنفسك ما إذا كان ينتج عن ذلك نتائج مفيدة ومثيرة للاهتمام. كما يقول المثل: “دليل جودة الطعام في تجربة أكله”.
المعرفة في نظرية الألعاب
إن مصطلح التفاعل الاستراتيجي في الواقع أكثر تشعبًا مما تمت الإشارة إليه أعلاه.
لا يكفي أن أعرف أن أفعالي، وكذلك أفعالك، تؤثر على النتيجة، ولكن يجب أن أعلم أيضًا أنك تعرف هذه الحقيقة. خذ مثال اثنين من مزارعي القمح.
افترض أن كلا من المزارع “أ” و “ب” يعلم أن اختيارات الأسعار الخاصة به ستؤثر على أرباحه لليوم. ولكن لنفترض أن “أ” لا يعرف أن “ب” يعرف ذلك.
الآن، من وجهة نظر المزارع “أ”، المزارع “ب” يجهل تمامًا ما يجري في السوق وبالتالي قد يحدد المزارع “ب” أي سعر. وهذا يجعل قرار المزارع “أ” غير مهم إلى حدِ ما.
لنمذجة الوضع بشكل أكثر واقعية، يتعين علينا بعد ذلك أن نفترض أنهم يعلمون أنهم يعرفون أن أسعارهم ستؤثر على أرباحهم.
يجب على المرء في الواقع أن يستمر بهذه الطريقة ويفترض أن قواعد اللعبة هي معرفة مشتركة، بما في ذلك كيفية تأثير الإجراءات على عقلانية المشاركين والأفراد.
الحقيقة X هي معرفة شائعة إذا كان الجميع يعرفها، إذا كان الجميع يعرف أن الجميع يعرفها، إذا كان الجميع يعرف أن الجميع يعرف أن الجميع يعرفها، إلخ. يحتوي هذا على مقدمة بعض الآثار الفلسفية ويخضع للكثير من الجدل، ولكن في الغالب سنتجنب هذه المناقشات ونأخذها على النحو المحدد.
باختصار، قد نحدد نظرية الألعاب على النحو التالي:
تعريف نظرية الألعاب
نظرية الألعاب (بالإنجليزية: Game Theory) هي دراسة منهجية للتفاعلات الاستراتيجية بين الأفراد العقلانيين.
بصرف النظر عن حدودها، تم تطبيق نظرية الألعاب بشكل مثمر على العديد من المواقف في عالم الاقتصاد والعلوم السياسية وعلم الأحياء والقانون وما إلى ذلك. في بقية هذا الفصل سنوضح الأفكار والمفاهيم الرئيسية لنظرية الألعاب وبعض تطبيقاتها باستخدام أمثلة بسيطة. في فصول لاحقة سنقوم بتحليل سيناريوهات أكثر واقعية ومعقدة ونناقش كيفية تطبيق نظرية الألعاب في العالم الحقيقي.
ومن بين هذه التطبيقات:
- المنافسة القوية في أسواق احتكار الندرة
- المنافسة بين الأحزاب السياسية
- المزادات العلنية
- المساومة
- التفاعل المتكرر بين الشركات
من أجل المقارنة، نبدأ أولا بمثال لا يوجد فيه تفاعل استراتيجي، وبالتالي لا يحتاج المرء إلى نظرية الألعاب لتحليلها.
مثال (1) لعبة قرار شخص واحد
افترض أن “علي” مستثمر يمكنه استثمار 100 دولار إما في أصل آمن، على سبيل المثال، السندات الحكومية، والتي تحقق عائدًا بنسبة 10٪ في عام واحد، أو يمكنه استثمارها في أصل محفوف بالمخاطر، مثلا الأسهم التي أصدرتها شركة ما، والتي تجلب إما عائد 20٪ (إذا كان أداء الشركة جيدًا) أو عائد صفري (إذا كان أداء الشركة سيئًا).
والجدول التالي يوضح تلك الخيارات:
| حالة الاستثمار | ||
| جيدة | سيئة | |
| السندات الحكومية | 10% | 10% |
| أسهم إحدى الشركات | 0 % | 20 % |
من الواضح أن الاستثمار الأفضل بالنسبة لعلي يعتمد على تفضيلاته وعلى الاحتمالات العامة.
دعونا نشير إلى احتمالية حدوث الحالة الجيدة (ص) والحالة السيئة (1− ص)، ونفترض أن “علي” يريد زيادة مبلغ المال إلى أقصى حد له في نهاية العام. إذا استثمر 100 دولار في السندات، فسيحصل على 110 دولارًا في نهاية العام بغض النظر عن الاحتمالات (أي على وجه اليقين). ومع ذلك، إذا استثمر في الأسهم، فمع الاحتمال (ص) سيكون لديه 120 دولارًا واحتمال (1-ص) سيحصل على 100 دولار.
وبالتالي يمكننا حساب متوسط حيازته من الأموال (أو المتوقعة) في نهاية العام كما يلي:
ص × 120 + (1− ص) × 100 = 100 + 20 × ص
إذا، مثلا، إذا كانت (ص = 0.5)، فإنه يُتوقع أن يكون لديه 110 دولارات في نهاية العام.
بشكل عام، إذا كانت (ص > 0.5)، فإنه يُفضل الاستثمار في الأسهم، وإذا كانت (ص < 0.5) فإنه يُفضل الاستثمار في السندات.
هذا مجرد مثال واحد لمشكلة اتخاذ القرار لشخص واحد، حيث يمكن تحليل مشكلة اتخاذ القرار للفرد بمَعزل عن سلوك الأفراد الآخرين.
أي عدم يقين في التفاعل في مثل هذه المشاكل هو أمر خارجي، بمعنى أنه لا يتحدد أو يتأثر بأي شكل من الأشكال بسلوك الفرد المعني.
في المثال أعلاه، يأتي عدم اليقين الوحيد من أداء السهم، والذي قد نفترض بكل تأكيد أنه مستقل عن اختيارات “علي” للاستثمار.
قارن ذلك بالحالة الموضحة في المثال التالي.
مثال (2) لعبة الاستثمار
الآن، لنفترض أن أمام “علي” خيارين لاستثمار 100 دولار. يجوز له إما استثمارها في السندات، التي لها عائد معين بنسبة 10٪، أو قد يستثمرها في مشروع محفوف بالمخاطر. يتطلب هذا المشروع 200 دولار ليكون ناجحًا، وفي هذه الحالة يكون العائد 20٪، أي أن استثمار كل 100 دولار ينتج عنه 120 دولارًا في نهاية العام. إذا كان إجمالي الاستثمار أقل من 200 دولار، فإن المشروع يكون فاشلًا ويحقق عائدًا صفريًا، أي أن استثمار 100 دولار فقط يُنتج 100 دولار. يعرف “علي” أن هناك شخصًا آخر، ليكن “بيريل”، وهي في نفس الوضع بالضبط، ولا يوجد مستثمر مُحتمل آخر في المشروع. لسوء الحظ، لا يعرف “علي” و”بيريل” بعضهما البعض ولا يمكنهما التواصل. لذلك، يجب على كلاهما اتخاذ قرار الاستثمار دون معرفة قرارات بعضهما البعض.
يمكننا تلخيص العوائد على استثمارات “علي” و”بيريل” كدالة لقراراتهما في الجدول الوارد في الشكل التالي، حيث يُمثل الرقم الأول في كل خلية العائد على استثمار “علي”، بينما يمثل الرقم الثاني العائد على استثمار “بيريل”.
نفترض أن كل من علي وبيريل يعرفان الوضع الممثل في هذا الجدول، أي أنهم يعرفون قواعد اللعبة.
| بيرل | بيرل | ||
| السندات | المشروع | ||
| علي | السندات | 110 – 110 | 110 – 100 |
| علي | المشروع | 100 – 110 | 120 – 120 |
تحليل لعبة الاستثمار
يُلاحظ في هذا المثال بوضوح وجود التفاعل الاستراتيجي، بالمقارنة مع الحالة في المثال (1) السابق.
العنصر الحاسم هو أن نتيجة قرار “علي” (عائد الاستثمار المُختار) تعتمد على ما تفعله “بيريل”.
الاستثمار في الخيار المحفوف بالمخاطر، أي الاستثمار في المشروع هنا، له عائد غير مؤكد، كما كان الحال في المثال (1). ومع ذلك، فإن مصدر عدم اليقين الآن هو فرد آخر، وهي “بيريل”. إذا اعتقد “علي” أن “بيريل” ستستثمر في المشروع، فإن اختياره الأمثل هو المشروع أيضًا، بينما إذا كان يعتقد أن “بيريل” ستستثمر في السندات، فإن خياره الأمثل هو الاستثمار في السندات. علاوة على ذلك، فإن “بيريل” في وضع مشابه، وهذه الحقيقة تجعل المشكلة مختلفة بشكل كبير عن تلك المذكورة في المثال (1) المتعلق بلعبة قرار شخص واحد.
لذا، ماذا يجب أن يفعل “علي”؟ ماذا تتوقع أن يحدث في هذه الحالة؟
في هذه المرحلة ليس لدينا معلومات كافية في نموذجنا لتقديم إجابة. أولا، يجب أن نصف أهداف “علي” و”بيريل”، أي تفضيلاتهما بالنسبة لمجموعة النتائج المحتملة. أحد الاحتمالات، وهي المفضلة لدى الاقتصاديين، هو افتراض أن كل منهما يرغب في تحقيق أفضل المكاسب أو المنافع. واذا اعتبرنا أن المنافع بالنسبة لهم هي كمية الأموال التي يمتلكونها، فقد نفترض أنهم يتوقعون زيادة حجم هذه الأموال. هذا، مع ذلك، لا يكفي بالنسبة لنا للإجابة على سؤال “علي”، لأننا يجب أن نعطيه طريقة لتكوين توقعات بشأن سلوك “بيريل”.
أحد الاحتمالات البسيطة هو افتراض أن “علي” يعتقد أن “بيريل” سوف تختار السندات مع احتمال معين تتراوح قيمته بين صفر وواحد. ثم، تصبح مشكلة قراره مماثلة لتلك الموجودة في المثال (1). في ظل هذا الافتراض، لا نحتاج إلى نظرية الألعاب لحل مشكلته. ولكن، هل يُعقل أن نفترض أن “بيريل” سوف تقرر بهذه الطريقة الآلية؟ لقد افترضنا بذلك أن “بيريل” تسعى لزيادة العائد النقدي المتوقع. لذا، لنفترض أنهما عقلانيان، أي أنهما يختاران الإجراء الذي يزيد من عوائدهما المتوقعة، وكلاهما يعرف أن الآخر عقلاني.
تحليل معمّق للعبة الاستثمار
ولكن هل هذا يكفي؟ يعرف “علي” أن “بيريل” عقلانية، لكن هذا لا يزال غير كافٍ بالنسبة له لاستنتاج ما سوف تفعله. وهو يعلم أنها ستفعل ما يزيد من عائدها المتوقع، والذي يعتمد بدوره على ما تعتقده هي عما سوف يفعله “علي”. لذلك، ما يجب أن يفعله “علي” يعتمد على ما يعتقد أن “بيريل” تعتقد أنه سيفعله. لذا، علينا أن نخطو خطوة أخرى ونفترض أنه ليس فقط كل منهما يعرف أن الآخر عقلاني ولكن يعرف كل منهما أيضًا أن الآخر يعرف أن الآخر عقلاني. يمكننا أن نستمر بهذه الطريقة لنجادل بأن الحل الذكي لحل لغز “علي” هو افتراض أن كلاهما يعرف أن كلاهما عقلاني؛ كلاهما يعرف أن كلاهما يعرف أن كلاهما عقلاني؛ كلاهما يعرف أن كلاهما يعرف أن كلاهما يعرف أن كلاهما عقلاني؛ وهكذا إلى ما لا نهاية. هذه مشكلة صعبة بالفعل وتتعامل نظرية الألعاب تمامًا مع هذا النوع من المشاكل.
موضوع مقترح للقراءة: مدخل إلى إدارة المخاطر المالية
موسوعة العلوم المالية والإدارية – مركز البحوث والدراسات متعدد التخصصات
يُقدم المثال التالي مشكلة أسهل نسبيًا في حلها.
مثال (3) معضلة السجناء
ربما يكون أفضل مثال معروف، والذي أصبح أيضًا مثلًا للعديد من المواقف الأخرى، هو معضلة السجناء. القصة حدثت كما يلي:
تم القبض على اثنين من المشتبه بهم ووضعهما في زنازين مختلفة قبل المحاكمة. مدعي المقاطعة، والذي هو متأكد تمامًا من أن كل منهما مذنب لكنه يفتقر إلى أدلة كافية، يُقدم لهم الصفقة التالية: إذا اعترف أي منهما وأدان الآخر، فسيتم الحكم على كل منهما، على سبيل المثال، 5 سنوات من السجن. وإذا اعترف أحدهما والآخر لم يعترف، فسوف يطلق سراحه لتعاونه مع السلطات ويُحكم على غير المعترف بالسجن لمدة 6 سنوات. وأخيرًا، إذا لم يعترف أي منهما، فإن كلا المشتبه بهما سيقضيان عامًا واحدًا في السجن.
يمكننا تمثيل هذه القصة على شكل جدول، حيث نفترض أن قضاء مدة سنة في السجن تُناظر الرقم (-1) لكل مشتبه به.
| اللاعب الثاني | اللاعب الثاني | ||
| س | ص | ||
| اللاعب الأول | س | -5 ، -5 | صفر ، -6 |
| اللاعب الأول | ص | -6 ، صفر | -1 ، -1 |
حيث يمثل الرمز (س) حالة الاعتراف، والرمز (ص) حالة عدم الاعتراف.
تحليل معضلة السجناء
على سبيل المثال، أفضل نتيجة للاعب الأول هي الحالة التي يعترف فيها ولا يعترف اللاعب الثاني، الحالة (س، ص).
النتيجة التالية الأفضل للاعب الأول هي عدم اعتراف الطرفين (ص، ص)، ثم (س، س) وأخيرًا (س، ص).
ينطبق تفسير مشابه على اللاعب الثاني. كيف ستلعب هذه اللعبة مكان اللاعب الأول؟
إحدى الملاحظات المفيدة هي ما يلي:
عند غض النظر عما ينوي اللاعب الثاني القيام به، فإن الاختيار (س) يُعطي نتائج أفضل للاعب الأول.
هذا لأن (س، س) نتيجة أفضل له من (ص، س)، و(س، ص) نتيجة أفضل له من (ص، ص).
لذا، يبدو أنه “عقلاني” فقط إذا اختار اللاعب الأول الاختيار (س) بالاعتراف.
يستدعي نفس المنطق للاعب الثاني، أي أن هذا اللاعب أيضًا من المحتمل جدًا أن يلعب بنفس الطريقة.
هناك توقع معقول جدًا هنا، وبالتالي، أن تنتهي اللعبة بالنتيجة (س، س)، والتي يعترف فيها كلا اللاعبين بجرائمهم.
وهذه هي المعضلة: ألن يكون كل لاعب أفضل حالًا من خلال لعب (ص) بدلا من (س)؟
قد تعتقد في البداية أن هذا الموقف ينشأ هنا فقط لأن السجناء يوضعون في زنازين منفصلة وبالتالي لا يُسمح لهم بالاتصال قبل اللعب. بالتأكيد، قد يثور الجدل حول ما إذا تناقش اللاعبون مُسبقًا عن كيفية لعب اللعبة، فسوف يدركون أن (ص، ص)، أفضل من (س، س) لكليهما، وبالتالي يوافقون على اختيار (ص) بدلا من (س). ولكن حتى إذا تم التوصل إلى مثل هذا الاتفاق اللفظي قبل اللعب الفعلي للعبة، فما الذي يجعل اللاعب الأول متأكدًا جدًا من أن اللاعب الثاني لن يطعنه في اللحظة الأخيرة من خلال اختيار الخيار (س)؛ وإذا اقتنع اللاعب الثاني بأن اللاعب الأول سيحتفظ حتى النهاية بالاختيار (ص)، فمن الأفضل له أن يختار (س). وبالتالي، حتى إذا تم التوصل إلى مثل هذا الاتفاق، فقد يخشى كلا اللاعبين بشكل معقول الخيانة، وبالتالي يلجأ إلى اختيار الخيانة قبل التعرض للخيانة واختيار (س)؛ لقد عدنا إلى المعضلة.
قيود إضافية في معضلة السجناء
السؤال هنا: ماذا تعتقد أنه سيحدث إذا تمكن اللاعبون من توقيع عقود مُلزمة؟
حتى إذا كنت مقتنعًا بوجود معضلة حقيقية هنا، فقد تتساءل لماذا نجعل مثل هذه الصفقة الكبيرة من قصة سخيفة. حسنًا، لاحظ أولا أن “قصة” معضلة السجناء ليست سوى قصة. المعضلة المعروضة أعلاه تتوافق مع سيناريوهات أكثر واقعية. النتيجة هي أن هناك حالات يؤدي فيها الاعتماد المتبادل بين الأفراد الذين يتبعون مصلحتهم الذاتية بشكل عقلاني إلى نتائج غير مرغوب فيها اجتماعيًا. بالنظر إلى أن أحد المزاعم الرئيسية للاقتصاد الكلاسيكي الجديد هو أن السعي الأناني لرفاهية الفرد يؤدي إلى نتائج فعّالة (اليد الخفية الشهيرة)، فإن هذه الملاحظة مهمة جدًا، والاقتصاديون يأخذونها على محمل الجد. نجد في معضلة السجناء دليلا لافتًا على حقيقة أن الادعاء الكلاسيكي بأن “السلوك اللامركزي يعني الكفاءة” ليس بالضرورة صالحًا في البيئات ذات المساحة الحقيقية للتفاعل الاستراتيجي.
تنشأ حالات معضلة السجناء في الواقع في العديد من السيناريوهات المثيرة للاهتمام، مثل سباقات التسلح، والمنافسة السعرية، وتسوية النزاعات مع المحامين أو بدونهم، وما إلى ذلك. والعنصر المشترك في جميع هذه السيناريوهات هو أنه إذا كان الجميع متعاونين، فإن النتائج تكون جيدة، ولكن لا أحد يجد في مصلحته الذاتية أن يعمل بشكل تعاوني، وهذا يؤدي إلى نتيجة أقل جاذبية.
لعبة التسعير (حالة خاصة من معضلة السجناء)
مثال تطبيقي على معضلة السجناء: لعبة التسعير في سوق القمح المحلي (الموضح في الجدول) حيث لا يوجد سوى مزارعين اثنين ويمكنهم إما تحديد سعر منخفض (ن) أو سعر مرتفع (ر).
فالمزارع الذي يحدد أقل سعر يلتقط السوق بالكامل، بينما إذا حدد الاثنين نفس السعر فإنهم يتقاسمون السوق بالتساوي.
| المزارع الثاني | المزارع الأول | ||
| ن | ر | ||
| المزارع الأول | ن | 1 – 1 | 4 – صفر |
| المزارع الأول | ر | صفر – 4 | 2 – 2 |
يرسم هذا المثال صورة قاتمة للغاية للتفاعلات البشرية. في الواقع، في كثير من الأحيان نلاحظ التعاون بدلا من الفشل الكامل. أحد المجالات المهمة للبحث في نظرية الألعاب هو تحليل البيئات والمؤسسات والمعايير، التي تدعم التعاون في الواقع في مواجهة مواقف يائسة مثل معضلة السجناء. فقط لتوضيح أحد هذه السيناريوهات، فكر في تكرار لعبة معضلة السجناء. في التفاعل المتكرر ، يجب على كل لاعب أن يأخذ في الاعتبار ليس فقط مردوده في كل تفاعل ولكن أيضًا كيف تؤثر نتائج كل من هذه التفاعلات على التفاعلات المستقبلية. على سبيل المثال، قد يحث كل لاعب على تعاون اللاعب الآخر من خلال اعتماد استراتيجية تُعاقب في كل مرة السلوك السيئ وتُكافئ السلوك الجيد.
مثال (4) لعبة الدجاج في نظرية الألعاب
في الفيلم الكلاسيكي الصادر عام 1955 بعنوان “Rebel Without a Cause“، الشخصيتان “جيم” (الممثل جيمس دين) و”باز” يتنافسان على الشخصية “جودي” (الممثلة ناتالي وود). يتجمّع أعضاء عصابة “باز” عبر جُرف يسقط في المحيط الهادئ. على “جيم” و”باز” القيادة نحو الجرف.
يتم تسمية أول شخص يقفز من سيارته بالدجاجة بينما آخر شخص يقفز يُسمى البطل ويحظى بقلب “جودي”.
لكل لاعب استراتيجيتين: القفز قبل اللاعب الآخر (ق) وبعد اللاعب الآخر (ب).
إذا قفزوا في نفس الوقت (ق، ق)، فإنهم سيبقون على قيد الحياة لكنهم يفقدون جودي.
إذا قفز أحدهما قبل والآخر بعده، فإن الأخير يعيش ويحصل على “جودي”، في حين أن الأول يعيش، ولكن بدون “جودي”.
أخيرًا، إذا اختار كلاهما القفز بعد الآخر (ب، ب)، فإنهما يموتان موتًا مُشرفًا.
يمكن تمثيل الحالة كما في الشكل التالي:
| باز | باز | ||
| ق | ب | ||
| جيم | ق | 2 – 2 | 1 – 3 |
| جيم | ب | 3 – 1 | صفر – صفر |
النتيجة المحتملة هنا غير واضحة. إذا اعتقد “جيم” أن “باز” سيقفز قبله، فمن الأفضل له الانتظار والقفز بعد ذلك. من ناحية أخرى، إذا كان يعتقد أن “باز” سينتظره، فمن الأفضل أن يقفز من قبل: فهو شاب وسيكون هناك فتيات أخريات مثل “جودي”. في الفيلم، كُم الجاكيت الجلد التي يرتديها “باز” عالق في مقبض باب سيارته. لا يستطيع القفز، على الرغم من أن “جيم” يمكنه القفز. كل من السيارة و”باز” يغرقان بالهاوية.
يتم استخدام لعبة الدجاج أيضًا كمثل للمواقف الأكثر إثارة للاهتمام من القصة المذكورة أعلاه. هناك إصدارات ديناميكية من لعبة الدجاج تُسمى حرب الاستنزاف. في لعبة حرب الاستنزاف، من المفترض أن يتخذ شخصان إجراءً والاختيار هو توقيت ذلك الإجراء. كلا اللاعبين يرغبون في أن يكونوا آخر من يتخذ هذا الإجراء.
على سبيل المثال، في لعبة الدجاج، العمل هو القفز. لذلك، يحاول كلا اللاعبين الانتظار لبعضهما البعض، ومن يستسلم أولا يخسر.
مثال (5) لعبة دخول السوق
في جميع الأمثلة حتى الآن، افترضنا أن اللاعبين إما يختارون استراتيجياتهم في وقت واحد أو دون معرفة اختيار اللاعب الآخر.
ونمذجة هذه المواقف تتم باستخدام ما يُعرف باسم ألعاب النماذج الاستراتيجية العادية.
ومع ذلك، في بعض المواقف، يُلاحظ اللاعبون على الأقل بعض التحركات التي قام بها لاعبون آخرون، وبالتالي فإن هذا ليس خيار النمذجة المناسب. خذ على سبيل المثال لعبة دخول السوق الموضحة في الشكل التالي. في هذه اللعبة تقرر شركة بيبسي (الرمز ب) أولا ما إذا كانت ستدخل سوقًا محتكرًا حاليًا بواسطة شركة كوكاكولا ( الرمز ك). بعد معرفة اختيار بيبسي، تقرر كوكاكولا ما إذا كانت ستحارب هذا الدخول ( الرمز ح)، على سبيل المثال، من خلال تخفيضات الأسعار و/ أو حملات الإعلان، أو أنها تقرر السماح به دون أي تحرُّك (الرمز س).
تتم نمذجة ألعاب التحركات المتسلسلة هذه باستخدام ما يعرف بألعاب النماذج الموسًعة.
ويمكن تمثيلها بشجرة ألعاب كما يظهر في الشكل التالي.
في هذا المثال، افترضنا أن بيبسي تُفضّل الدخول فقط إذا كانت كوكاكولا ستُذعن، وتُفضل كوكاكولا أن تظل محتكرة، ولكن إذا حدث الدخول من بيبسي، فإنها تفضل الإذعان؛ تم التعبير عن المكاسب في كل حالة بالأرقام المبينة على العُقد في الشكل التالي:
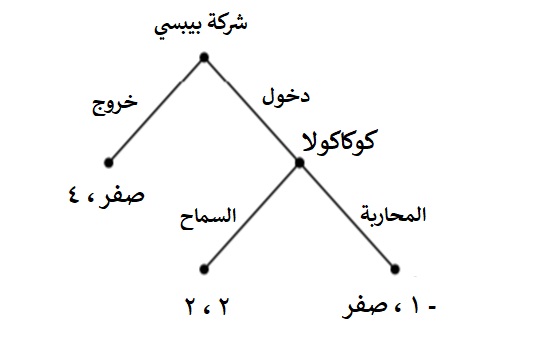
والآن، ماذا تعتقد أن تفعل شركة بيبسي؟
وهل هناك طريقة أمام كوكاكولا لتتجنب الدخول؟
مثال (6) لعبة الاستثمار بمعلومات غير كاملة
حتى الآن، في جميع الأمثلة السابقة، افترضنا أن كل لاعب يعرف كل شيء عن اللعبة، بما في ذلك تفضيلات اللاعبين الآخرين. لكن الواقع ليس بهذه البساطة. في العديد من المواقف، نفتقر إلى المعلومات ذات الصلة فيما يتعلق بالعديد من مكونات الموقف الاستراتيجي، مثل هوية وتفضيلات اللاعبين الآخرين، والاستراتيجيات المُتاحة لنا وللاعبين الآخرين، وما إلى ذلك. تُعرف هذه الألعاب باسم الألعاب ذات المعلومات غير الكاملة أو الألعاب الخاصة.
كمثال توضيحي، دعنا نعود إلى المثال رقم (2)، الذي نقوم بتعديله بافتراض أن “علي” غير متأكد من تفضيلات “بيريل”. على وجه الخصوص، افترض أنه يعتقد (مع احتمال بقيمة = ح) أن “بيريل” لديها تفضيلات ممثلة في الجدول الأول (الوضع الطبيعي)، ومع الاحتمال المُقابل بقيمة =(1-ح) هو يعتقد أن “بيريل” مجنونة قليلا ولديها بعض الميل المتأصل في المخاطرة والمُمثلة في الجدول الثاني (وضع المخاطرة)، حتى إذا كانت غير معقولة من منظور المستثمر العقلاني.
يمكن تمثيل الوضع الجديد في الجدولين التاليين:
| بيرل | |||
| السندات | المشروع | ||
| علي | السندات | 110 – 110 | 110 – 100 |
| المشروع | 100 – 110 | 120 – 120 |
| بيرل | |||
| السندات | المشروع | ||
| علي | السندات | 110 – 110 | 110 – 120 |
| المشروع | 100 – 110 | 120 – 120 |
تحليل لعبة الاستثمار
إذا كان “علي” متأكدًا من أن “بيريل” مُغامرة، فسيكون اختياره واضحًا: يجب عليه اختيار الاستثمار في المشروع. إلى أي مدى يجب أن يكون الحل في هذه اللعبة باتخاذ نفس القرار من “علي” و”بيرل”، بغض النظر عن تفضيلاتها، وهو الاستثمار في المشروع؟ افترض أن “بيريل” (العادي غير المُغامر) يختار السندات، ويعتقد “علي” أن هذا هو الحال. الاستثمار في السندات ينتج عنه 110 دولارات لـ “علي” بغض النظر عما تفعله “بيريل”. أما الاستثمار في المشروع، مع ذلك، يكون فيه العائد المتوقع التالي لـ “علي”:
ح × 100 + (1-ح) × 120 = 120 – 20 ح
وهذا العائد هو أكبر من 110 دولارات فقط إذا كانت:
ح < 0.5
بعبارة أخرى، فإننا نتوقع أن يكون الحل هو الاستثمار في المشروع لكلا اللاعبين إذا كان اعتقاد “علي” بأن “بيريل” مجنونة وتميل للمغامرة في الاستثمار هو قوي بما فيه الكفاية.
مثال (7) عمليات الاستحواذ العدائية
خلال الثمانينيات، كانت هناك موجة ضخمة من عمليات الاندماج والاستحواذ في الولايات المتحدة. اتخذ العديد من عمليات الاستحواذ شكل “عمليات الاستحواذ العدائية”، وهو مصطلح يستخدم لوصف عمليات الاستحواذ التي يتم تنفيذها ضد إرادة إدارة الشركة المستهدفة. عادة ما تتخذ شكل عروض مناقصة مباشرة للمساهمين، أي أن المستحوذ يقدم علانية سعرًا لجميع المساهمين. كانت بعض عروض المناقصات هذه على شكل ما يعرف باسم “عروض المناقصات ذات المستويين”.
كان هذا هو الحال في عام 1988 عندما قدم “روبرت كامبو” عرضًا للعطاء للمتاجر الفيدرالية.
دعونا نفكر في نسخة مبسطة من القصة الفعلية. لنفترض أن سعر الشراء المسبق للسهم المتحد هو 100 دولار. عرض “كامبو” دفع 105 دولارات لكل سهم مقابل الـ 50٪ الأولى من الأسهم، ودفع 90 دولارًا للباقي. ومع ذلك، يتم شراء جميع الأسهم بمتوسط سعر إجمالي الأسهم المطروحة. إذا نجح الاستحواذ، فإن الأسهم التي لم يتم تقديمها تساوي 90 دولارًا لكل منها.
على سبيل المثال، إذا تم طرح 75٪ من الأسهم، فإن “كامبو” يدفع 105 دولارات مقابل الـ 50٪ الأولى ويدفع 90 دولارًا مقابل الـ 25٪ المتبقية. متوسط السعر الذي يدفعه “كامبو” = (م)، حيث:
م = 105 × (50 ÷ 75) + 90 × (25÷75)
وبشكل عام، إذا تم طرح نسبة مئوية من الأسهم (س)، فإن متوسط السعر المدفوع لسعر السهم المقدم (م)، يتم حسابه بواسطة إحدى العلاقات التالية:
الحالة الأولى
إذا كانت النسبة المئوية لعدد الأسهم (س) أقل من أو تساوي 50%، فإن:
م = 105
الحالة الثانية
إذا كانت النسبة المئوية لعدد الأسهم (س) أكبر من 50%، فإن:
م = 105 × (50 ÷ س) + 90 × (س-50) ÷ 75
لاحظ أنه إذا تم طرح كل الأسهم بالمناقصة، أي أن (س) = 100، فإن “كامبو “يدفع 97.5 دولارًا للسهم الواحد وهو أقل من سعر السوق الحالي. لذا، تبدو هذه صفقة جيدة له، ولكن فقط إذا كان عدد كبير من المساهمين تقدموا للعطاء.
إذا كنت من المساهمين الفيدراليين، فهل ستقدم أسهمك إلى “كامبو”؟
هل تعتمد إجابتك على ما تعتقد أن المساهمين الآخرين سيفعلونه؟
افترض الآن أن عروض “ماسي” تُقدم بمبلغ 102 دولارًا للسهم الواحد مشروطة عند الحصول على الأغلبية. ماذا كنت ستفعل؟
كان الكشف عن الأحداث الفعلي مؤسفًا تمامًا لـ “كامبو”. انضمت شركة “ماسي” إلى المزايدة وزاد هذا من القيمة بشكل ملحوظ. فاز “كامبو” أخيرًا (ليس من خلال عرض مناقصة ذي مستويين) لكنه دفع 8.17 مليار دولار لشراء أسهم شركة بقيمة استحواذ مسبقة مقدارها 2.93 مليار دولار. موَّل “كامبو” 97 في المئة من سعر الشراء بالدين. بعد أقل من عامين، أفلست المتاجر الفيدرالية وفقد “كامبو” وظيفته.
خلاصة نظرية الألعاب
رأينا أن العديد من المواقف المثيرة للاهتمام تنطوي على تفاعلات استراتيجية بين الأفراد، وبالتالي تجعلهم محل دراسة نظرية الألعاب.
عند هذه النقطة أمامنا خياران، يمكننا إما تحليل كل حالة على حدة أو قد نحاول العثور على المبادئ العامة التي تنطبق على أي لعبة.
توفر نظرية الألعاب أدوات لتحليل التفاعلات الاستراتيجية، والتي يمكن تطبيقها بعد ذلك على أي موقف يشبه كل لعبة.
المصدر
- An Introduction to Game Theory, Levent Kocesen (Koc University) and Efe A. Ok (New York University), July 8, 2007
- مقدمة في نظرية الألعاب، ترجمة وإعداد: د. م. مصطفى عبيد، إصدار: مركز البحوث والدراسات متعدد التخصصات، 2020م