معادلات الحركة والتفاضل والتكامل

بنهاية هذا القسم الخاص بموضوع معادلات الحركة والتفاضل والتكامل واستخدامه في إيجاد السرعة والإزاحة من التسارع، سيكون القارئ قادرًا على:

اشتقاق معادلات الحركة في تسارع ثابت باستخدام حساب التفاضل والتكامل.
استخدام الصيغة المتكاملة لمعادلات الحركة في تحليل الحركة.
إيجاد شكل دالة السرعة بدلالة الزمن وفقًا لدالة التسارع.
إيجاد شكل دالة الموضع بدلالة الزمن بالنظر إلى دالة السرعة.

يفترض هذا القسم أن لديك خلفية كافية في حساب التفاضل والتكامل لتكون على دراية بالتكامل. في السرعة والسرعة اللحظية، ومتوسط التسارع والتسارع اللحظي، قدمنا الدوال الحركية للسرعة والتسارع باستخدام الاشتقاق. بأخذ مشتقة دالة الموضع، وجدنا دالة السرعة، وبالمثل بأخذ مشتقة دالة السرعة وجدنا دالة التسارع. باستخدام حساب التفاضل والتكامل، يمكننا العمل للخلف وحساب دالة السرعة من دالة التسارع أو العجلة، وحساب دالة الموضع من دالة السرعة.

المحتويات

معادلات الحركة من حساب التفاضل والتكامل

لنبدأ بجسيم يسير بتسارع a (t) وهي دالة بمعرفة الزمن. بما أن المشتق الزمني لدالة السرعة هو التسارع، أي أن:

\frac{d}{d t} v (t) = a (t),

يمكننا أخذ التكامل غير المحدود لكلا الطرفين، ينتج لنا:

\int \frac{d}{d t} v (t) d t = \int a (t) d t + C_{1},

حيث C₁ هو ثابت التكامل.

ثم أن:

\int \frac{d}{d t} v (t) d t = v (t)

حساب السرعة

بالتعويض في معادلة التكامل، تنتج لنا السرعة كما يلي:

v (t) = \int a (t) d t + C_{1} .

(3.18)

حساب الإزاحة

وبالمثل، نظرًا لأن المشتقة بالنسبة للزمن لدالة الموضع هو دالة السرعة:

\frac{d}{d t} x (t) = v (t) .

وبالتالي، يمكننا استخدام نفس الأسلوب الرياضي الذي استخدمناه للتو، وسوف نجد أن:

x (t) = \int v (t) d t + C_{2},

(3.19)

حيث C₂ هو ثابت التكامل الثاني.

ثم يمكننا اشتقاق معادلات الحركة بتسارع ثابت باستخدام هذه التكاملات.

مع الحركة بتسارع ثابت a(t) = a، نقوم بإجراء التكامل في المعادلة 3.18، ينتج لنا:

v (t) = \int a d t + C_{1} = a t + C_{1} .

إذا كانت السرعة الابتدائية v(0) = v₀، إذن يصبح لدينا:

v₀ = 0 + C₁

أي أن: C₁ = v₀، ثم كذلك:

v(t) = v₀ + at

وهي معادلة الحركة رقم 3.12.

وبالتعويض عن قيمة v(t) في المعادلة 3.19 ينتج لنا:

x (t) = \int (v_{0} + a t) d t + C_{2} .

ثم عند القيام بالتكامل، ينتج لنا:

x(t) = v₀ t + 1/2 at² + C₂

ثم إذا كانت x (0) = x₀، يكون لدينا:

x₀ = 0 + 0 + C₂

لذلك، يكون C₂ = x₀.

الآن بالتعويض مرة أخرى في المعادلة عن قيمة x (t)، يصبح لدينا أخيرًا:

x (t) = x_{0} + v_{0} t + \frac{1}{2} a t^{2},

وهي معادلة الحركة رقم 3.13.

مثال 3.17: حركة زورق بخاري

يسير زورق بمحرك بسرعة ثابتة تبلغ 5 متر / ثانية عندما يبدأ في التباطؤ للوصول إلى الرصيف. مقدار العجلة أو التسارع تحدده الدالة:

a(t) = – (1/4) t m/s³

(أ) ما هي دالة السرعة للزورق البخاري؟ (ب) في أي وقت تصل السرعة إلى الصفر؟ (ج) ما هي دالة موضع الزورق البخاري؟ (د) ما هي إزاحة الزورق من الوقت الذي يبدأ فيه في التباطؤ إلى أن تصبح السرعة صفرًا؟ (هـ) ارسم دالة السرعة والموضع.

إستراتيجية الحل

(أ) للحصول على دالة السرعة، يجب علينا إجراء التكامل واستخدام المعطيات الأولية لإيجاد ثابت التكامل. (ب) نجعل دالة السرعة تساوي صفرًا ونوجد قيمة الزمن t. (ج) بالمثل، يجب أن نجري التكامل لإيجاد دالة الموضع واستخدام المعطيات الأولية لإيجاد ثابت التكامل. (د) بما أن الموضع الأولي يعتبر صفرًا، فلا يتعين علينا سوى حساب دالة الموضع عند t = 0.

الحل

نعتبر أن t = 0 هو الوقت الذي يبدأ فيه القارب في التباطؤ.

أ. حساب السرعة

من نموذج دالة التسارع يمكننا حل المعادلة 3.18 للحصول على v (t):

v (t) = \int a (t) d t + C_{1} = \int - \frac{1}{4} t d t + C_{1} = - \frac{1}{8} t^{2} + C_{1} .

عند t = 0 لدينا:

v (0) = 5 m/s = 0 + C₁

لذا يكون: C1 = 5 m/s

ثم بالتالي يكون:

v (t) = 5 m/s − 1/8 t²

ب: حساب الزمن

v(t) = 0 = 5 m/s – 1/8 t² m/s³ ⇒ t = 6.3 s

ج. دالة الموضع

بحل المعادلة 3.19:

x (t) = \int v (t) d t + C_{2} = \int (5.0 - \frac{1}{8} t^{2}) d t + C_{2} = 5.0 t m/s - \frac{1}{24} t^{3} m/ s^{3} + C_{2} .

عند t = 0، قمنا بتعيين x(0) = 0 = x₀، نظرًا لأننا مهتمون فقط بالإزاحة من الوقت الذي يبدأ فيه القارب في التباطؤ. لدينا:

x(0) = 0 = C₂

لذلك، فإن معادلة الموضع هي:

x(t) = 5 t – 1/24 t³

د. حساب الإزاحة

نظرًا لأن الموضع الأولي يساوي صفرًا، فلا يتعين علينا سوى حساب دالة الموضع في الوقت الذي تكون فيه السرعة صفرًا. يحدث هذا عند t = 6.3 ثانية. لذلك، فإن الإزاحة يمكن حسابها كما يلي:

x(6.3) = 5(6.3 s) – 1/24 (6.3 s) = 21.1 m

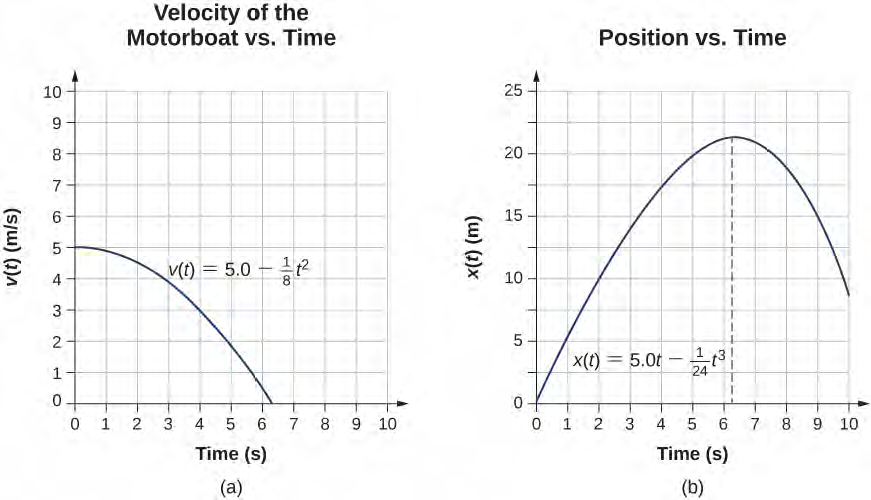
الشكل 3.30: معادلات الحركة والتفاضل والتكامل - شكل دالة السرعة ودالة الموضع لزورق بخاري يسير بتسارع ثابت — الشكل 3.30: معادلات الحركة والتفاضل والتكامل، شكل دالة السرعة ودالة الموضع لزورق بخاري يسير بتسارع ثابت

ه. في الشكل 3.30 (أ) سرعة الزورق البخاري كدالة للزمن. يقلل الزورق من سرعته إلى صفر في 6.3 ثوانٍ. وفي أوقات أكبر من ذلك، تصبح السرعة سالبة – بمعنى أن القارب ينعكس اتجاهه، (ب) موقف الزورق البخاري كدالة للوقت، عند t = 6.3 s، تكون السرعة صفرًا ويتوقف القارب، في أوقات أكبر من ذلك، تصبح السرعة سالبة – بمعنى أنه إذا استمر القارب في التحرك بنفس التسارع، فإنه ينعكس اتجاهه ويتجه عائدًا نحو المكان الذي بدأ فيه

الدلالة

تكون دالة التسارع أو العجلة خطية بدلالة الزمن، لذا فإن تكامل هذه الدالة يتضمن كثيرات حدود بسيطة. في الشكل 3.30، نرى أنه إذا قمنا بتمديد الحل إلى ما بعد النقطة التي تكون فيها السرعة صفرًا، تصبح السرعة سالبة ويعكس القارب اتجاهه. يخبرنا هذا أن الحل يمكن أن يزودنا بمعلومات خارج نطاق اهتمامنا المباشر أو المطلوب في المسألة ويجب أن نكون حذرين عند تفسيرها.

تأكد من فهمك معادلات الحركة والتفاضل والتكامل

يبدأ جسيم بالحركة من السكون وله دالة تسارع هي: a(t) = 5 – 10 t m/s²

(أ) ما هي دالة السرعة؟ (ب) ما هي دالة الموضع؟ (ج) متى تكون السرعة صفرًا؟

المصدر

موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.