قانون نيوتن الثالث

قانون نيوتن الثالث

لقد اعتبرنا القوة حتى الآن بمثابة دفع أو شد. ومع ذلك، إذا فكرت في الأمر، ستدرك أنه لا يحدث أي دفع أو شد من تلقاء نفسه. عندما تضغط على الحائط، يدفعك الجدار للخلف. يقودنا هذا إلى قانون نيوتن الثالث.

أهداف التعلم:

بنهاية قسم قانون نيوتن الثالث ستكون قادرًا على:

• نص قانون نيوتن الثالث للحركة
• تحديد قوى الفعل ورد الفعل في المواقف المختلفة
• تطبيق قانون نيوتن الثالث لتعريف الأنظمة وحل مسائل الحركة

نص قانون نيوتن الثالث للحركة

عندما يمارس أحد الأجسام قوة على جسم آخر، يتعرض الجسم الأول لقوة مساوية في الحجم ومعاكسة في اتجاه القوة التي يبذلها. رياضيًا، إذا مارس الجسم A القوة F⃗ على الجسم B، فإن B في نفس الوقت يمارس القوة -F⃗ على الجسم A، أو في شكل معادلة متجهة:

(5.10)

يمثل قانون نيوتن الثالث تناظرًا محددًا في الطبيعة: توجد القوى دائمًا في أزواج، ولا يمكن لجسم ما أن يمارس قوة على الآخر دون أن يختبر القوة نفسها. نشير أحيانًا إلى هذا القانون بشكل فضفاض على أنه “لكل فعل رد فعل”، حيث تكون القوة المبذولة هي الفعل والقوة التي يتم اختبارها كنتيجة هي رد الفعل. قانون نيوتن الثالث له استخدامات عملية في تحليل أصل القوى وفهم القوى الخارجية للنظام.

يمكننا أن نرى بسهولة قانون نيوتن الثالث في العمل من خلال إلقاء نظرة على كيفية تحرك الناس. مثال على ذلك السبّاح عندما يدفع جانب حمام السباحة (الشكل 5.16). يضغط على جدار المسبح بقدميه ويتسارع في الاتجاه المعاكس لاتجاه دفعه. لقد مارس الجدار قوة مساوية ومعاكسة للسباح. قد تعتقد أن قوتين متساويتين ومتعاكستين ستلغيان بعضهما البعض، لكنهما لا يفعلان ذلك لأنهما يعملان على أنظمة مختلفة. في هذه الحالة، هناك نظامان يمكننا التحقيق فيهما: السباح والجدار.

اختيار النظام وتحديد القوى

إذا اخترنا السباح ليكون نظام الاهتمام، كما في الشكل، فإن F _{wall on feet} هي قوة خارجية على هذا النظام وتؤثر على حركته. السباح يتحرك في اتجاه هذه القوة. في المقابل، فإن القوة F _{feet on wall} تعمل على الحائط، وليس على نظام اهتمامنا. وبالتالي، لا تؤثر F _{feet on wall} بشكل مباشر على حركة النظام ولا تلغي F _{wall on feet}. السباح يدفع بقدميه في الاتجاه المعاكس للاتجاه الذي يرغب في التحرك فيه. وبالتالي فإن رد الفعل على دفعه يكون في الاتجاه المطلوب. في مخطط الجسم الحر، مثل الرسم الموضح في الشكل 5.16، لا نقوم أبدًا بتضمين كلتا قوتَي زوج الفعل ورد الفعل؛ في هذه الحالة، نستخدم F _{wall on feet} فقط، وليس F _{feet on wall}.

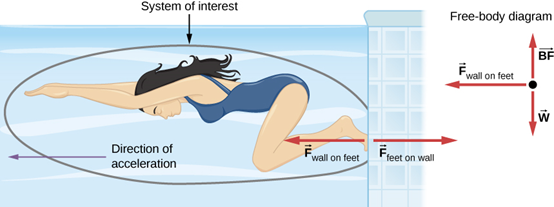
في الشكل 5.16، عندما يمارس السباح قوة على الحائط، فإنه يتسارع في الاتجاه المعاكس؛ بمعنى آخر، القوة الخارجية الصافية عليه في الاتجاه المعاكس لاتجاه F _{feet on wall}. يحدث هذا التعارض لأنه، وفقًا لقانون نيوتن الثالث، يمارس الجدار قوة F _{wall on feet} على السباح تساوي في المقدار ولكن في الاتجاه المعاكس للقوة التي يمارسها هو على الجدار. يشير الخط المحيط بالسباح إلى نظام الاهتمام. وبالتالي، فإن مخطط الجسم الحر يُظهر فقط F _{wall on feet}، وw (قوة الجاذبية)، وBF، وهي قوة طفو الماء التي تدعم وزن السباح. تلغي القوى الرأسية w وBF لعدم وجود تسارع رأسي.

أمثلة واقعية على قانون نيوتن الثالث

من السهل العثور على أمثلة أخرى لقانون نيوتن الثالث:

• بينما يسير الأستاذ أمام السبورة، يبذل قوة للخلف على الأرض. تمارس الأرضية قوة رد فعل للأمام على الأستاذ تجعله يسرع للأمام.
• تتسارع السيارة للأمام لأن الأرض تندفع للأمام على عجلات القيادة، كرد فعل على دفع عجلات القيادة للخلف على الأرض. يمكنك أن ترى دليلاً على دفع العجلات للخلف عندما تدور الإطارات على طريق من الحصى وترمي الصخور للخلف.
• الصواريخ تتحرك إلى الأمام عن طريق طرد الغاز إلى الوراء بسرعة عالية. هذا يعني أن الصاروخ يمارس قوة دفع خلفية كبيرة على الغاز في غرفة احتراق الصاروخ. لذلك، يبذل الغاز قوة رد فعل كبيرة للأمام على الصاروخ. تسمى قوة رد الفعل هذه، التي تدفع الجسم إلى الأمام استجابةً لقوة خلفية، بالدفع. من المفاهيم الخاطئة الشائعة أن الصواريخ تدفع نفسها بالدفع على الأرض أو في الهواء خلفها. إنهم في الواقع يعملون بشكل أفضل في الفراغ، حيث يمكنهم طرد غازات العادم بسهولة أكبر.
• تخلق المروحيات قوة الرفع عن طريق دفع الهواء لأسفل، وبالتالي تتعرض لقوة رد فعل تصاعدية.
• تطير الطيور والطائرات أيضًا عن طريق الضغط على الهواء في اتجاه معاكس لأي قوة يحتاجونها. على سبيل المثال، تدفع أجنحة الطائر الهواء للأسفل وللخلف للرفع والتحرك للأمام.
• يدفع الأخطبوط نفسه في الماء عن طريق إخراج الماء عبر قمع من جسمه، على غرار الدراجة المائية.
• عندما يسحب الشخص حبلًا رأسيًا، يشد الحبل لأعلى (الشكل 5.17).

الشكل 5.17: صورة لمتسلق الجبال على اليسار، ومخطط الجسم الحر على اليمين. السهم الذي يشير لأسفل (متسلق يسحب الحبل لأسفل). السهم المتجه لأعلى (الحبل يسحب المتسلق لأعلى). عندما يسحب متسلق الجبال الحبل لأسفل، يشد الحبل متسلق الجبال باتجاه الأعلى. (المصدر: كريستيان بورتس).

سمات قانون نيوتن الثالث

هناك سمتان مهمتان لقانون نيوتن الثالث. أولاً، القوى المبذولة (الفعل ورد الفعل) دائمًا ما تكون متساوية في المقدار ولكنها متعاكسة في الاتجاه. ثانيًا، تعمل هذه القوى على أجسام أو أنظمة مختلفة: تعمل قوة A على B وتعمل قوة B على A. وبعبارة أخرى، فإن القوتين هما قوتان منفصلتان لا تعملان على نفس الجسم. وبالتالي، فإنهم لا يلغون بعضهم البعض.

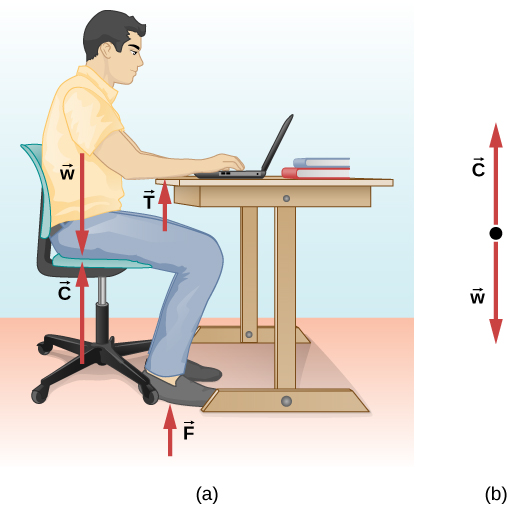
بالنسبة للموقف الموضح في الشكل 5.6، يشير القانون الثالث إلى أنه نظرًا لأن الكرسي يدفع الصبي للأعلى بقوة C⃗، فإن الطفل يدفع للأسفل على الكرسي بقوة -C⃗. وبالمثل، فهو يدفع لأسفل بقوة -F⃗ و-T⃗ على الأرض والطاولة، على التوالي. أخيرًا، نظرًا لأن الأرض تسحب للأسفل على الصبي بقوة w⃗، فإنه يسحب لأعلى على الأرض بقوة -w⃗. إذا قام هذا الطالب بضرب الطاولة بغضب في لحظة إحباط، فسوف يتعلم بسرعة الدرس المؤلم (الذي يمكن تجنبه من خلال دراسة قوانين نيوتن) أن الطاولة سوف ترد عليه بنفس القدر من الألم.

الشخص الذي يمشي أو يركض يطبق قانون نيوتن الثالث غريزيًا. على سبيل المثال، العدّاء في الشكل 5.18 يدفع للخلف على الأرض بحيث ترد هي بدفعه للأمام.

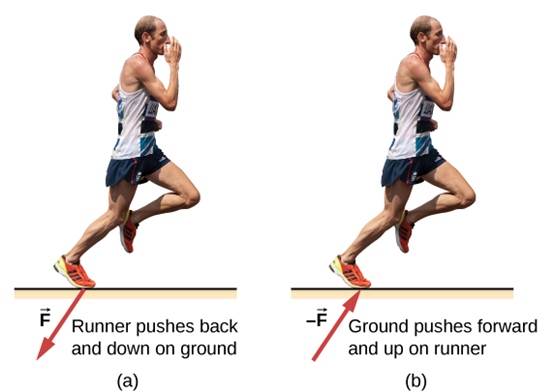
الشكل 5.18: العداء يطبق قانون نيوتن الثالث. (أ) القوة التي يبذلها العداء على الأرض. (ب) قوة رد فعل الأرض على العداء تدفعه إلى الأمام. (المصدر “العداء”: بواسطة “غرينتش فوتوغرافي”، فليكر).

أمثلة وتطبيقات على قانون نيوتن الثالث

مثال 5.9: القوى المؤثرة على جسم ثابت

العبوة في الشكل 5.19 موجودة على ميزان. القوى الموجودة على العبوة هي S⃗ ، والتي ترجع إلى الميزان، و-w⃗، والتي ترجع إلى مجال الجاذبية الأرضية. قوى رد الفعل التي تمارسها العبوة هي S⃗ على الميزان وw⃗ على الأرض. لأن العبوة لا تتسارع، ينتج عن تطبيق القانون الثاني:

لذا فإن:

وبالتالي، فإن قراءة الميزان تعطي مقدار وزن العبوة. ومع ذلك، فإن الميزان لا يقيس وزن العبوة؛ يقيس القوة -S⃗ على سطحه. إذا كان النظام يتسارع، فلن يكون S⃗ و -w⃗ متساويين، كما هو موضح في تطبيقات قوانين نيوتن.

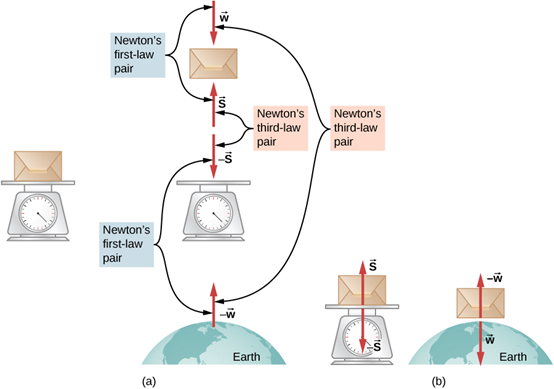
في الشكل 5.19: (أ) تظهر القوى الموجودة على العبوة في الميزان مع قوى رد الفعل الخاصة بها. القوة w هي وزن العبوة (القوة بسبب جاذبية الأرض) والقوة S⃗ هي قوة الميزان على العبوة. (ب) يؤدي عزل نظام (الميزان – العبوة) ونظام (العبوة – الأرض) إلى توضيح أزواج القوى والتفاعل بينها.

مثال 5.10: الحصول على السرعة: اختيار النظام الصحيح

يدفع أستاذ الفيزياء عربة من معدات العرض إلى قاعة المحاضرات (الشكل 5.20). كتلتها 65.0 كجم، وكتلة العربة 12.0 كجم، وكتلة المعدات 7.0 كجم. احسب التسارع الناتج عندما يبذل الأستاذ قوة رجعية مقدارها 150 نيوتن على الأرض. جميع القوى التي تعارض الحركة، مثل الاحتكاك بعجلات العربة ومقاومة الهواء، بإجمالي 24.0 نيوتن.

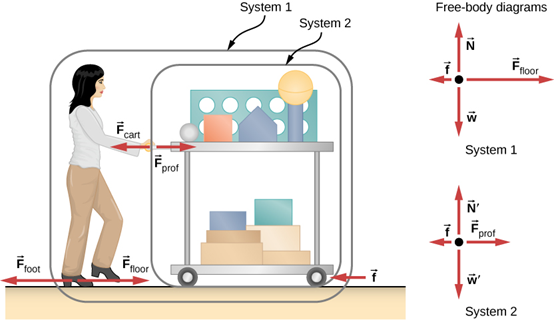
في الشكل 5.20: أستاذ يدفع العربة بمعداتها التوضيحية. أطوال الأسهم متناسبة مع مقادير القوى (باستثناء f⃗، لأنها صغيرة جدًا بحيث لا يمكن رسمها على نطاق واسع). النظام 1 مناسب لهذا المثال، لأنه يطلب تسريع مجموعة الكائنات بأكملها. فقط F⃗ _floor وf⃗ هما قوى خارجية تعمل على النظام 1 على طول خط الحركة. جميع القوى الأخرى إما تلغي أو تعمل على العالم الخارجي. تم اختيار النظام 2 للمثال التالي بحيث يكون F⃗ _prof قوة خارجية وتدخل في قانون نيوتن الثاني. تختلف مخططات الجسم الحر، التي تعمل كأساس لقانون نيوتن الثاني، باختلاف النظام المُختار.

إستراتيجية الحل

نظرًا لأنها تتسارع كوحدة واحدة، فإننا نحدد النظام ليكون (الأستاذ والعربة والمعدات). هذا هو النظام 1 في الشكل 5.20. يدفع الأستاذ للخلف بقوة قدمه F_foot مقدارها 150 نيوتن. وفقًا لقانون نيوتن الثالث، تمارس الأرضية قوة رد فعل أمامية F_floor مقدارها 150 نيوتن على النظام 1. نظرًا لأن كل الحركة أفقية، يمكننا أن نفترض أنه لا توجد قوة صافية في الاتجاه العمودي. لذلك، فإن المسألة أحادية البعد على طول الاتجاه الأفقي. كما لوحظ، فإن الاحتكاك f يعارض الحركة وبالتالي يكون في الاتجاه المعاكس لـ F_floor. لا نقوم بتضمين قوى F_prof أو F_cart لأن هذه قوى داخلية، ولا نقوم بتضمين F_foot لأنها تعمل على الأرض وليس على النظام. لا توجد قوى مهمة أخرى تعمل على النظام 1. إذا أمكن إيجاد القوة الخارجية الصافية من كل هذه المعلومات، فيمكننا استخدام قانون نيوتن الثاني لإيجاد التسارع على النحو المطلوب. انظر الرسم التخطيطي للجسم الحر في الشكل.

الحل

قانون نيوتن الثاني مُعطى بواسطة المعادلة:

a = F_net / m

يتم استنتاج صافي القوة الخارجية على النظام 1 من الشكل 5.20 والمناقشة السابقة، سيكون لدينا:

F_net = F_floor – f = 150 N – 24 N = 126 N

كتلة النظام 1 هي

m = (65 + 12 + 7 ) kg = 84 kg

تنتج قيم F_net وm تسارعًا قيمته:

الدلالة

لا تساهم أي من القوى بين مكونات النظام 1، مثل تلك التي بين يدي الأستاذ والعربة، في صافي القوة الخارجية لأنها داخلية للنظام 1. وهناك طريقة أخرى للنظر إلى هذا وهي أن القوى بين مكونات النظام تلغي بسبب أنهم متساوون في المقدار ومتعاكسون في الاتجاه. على سبيل المثال، القوة التي يبذلها الأستاذ على العربة ينتج عنها قوة مساوية ومعاكسة على الأستاذ. في هذه الحالة، تعمل كلتا القوتين على نفس النظام وبالتالي تلغي بعضها البعض. وهكذا، تلغي القوى الداخلية (بين مكونات النظام). كان اختيار النظام 1 أمرًا حاسمًا لحل هذه المسألة.

مثال 5.11: القوة على العربة: اختيار نظام جديد

احسب القوة التي يبذلها الأستاذ على العربة في الشكل 5.20، باستخدام بيانات من المثال السابق إذا لزم الأمر.

إستراتيجية الحل

إذا حددنا نظام الاهتمام على أنه العربة بالإضافة إلى المعدات (النظام 2 في الشكل 5.20)، فإن صافي القوة الخارجية على النظام 2 هو القوة التي يبذلها الأستاذ على العربة مطروحًا منها الاحتكاك. القوة التي يمارسها الأستاذ على العربة، F_prof، هي قوة خارجية تعمل على النظام 2. كانت القوة F_prof داخلية بالنسبة للنظام 1، لكنها الآن قوة خارجية بالنسبة للنظام 2 وبالتالي يدخل قانون نيوتن الثاني لهذا النظام.

الحل

يمكن استخدام قانون نيوتن الثاني لإيجاد F_prof. نبدأ بـ

a = F_net / m

مقدار صافي القوة الخارجية على النظام 2 هو:

F_net = F_prof − f

نحل المعادلة لإيجاد المطلوب وهو F_prof:

F_prof = F_net + f

تم إعطاء قيمة f، لذلك يجب علينا حساب F_net. يمكن القيام بذلك لأن كلا من تسارع وكتلة النظام 2 معروفان. باستخدام قانون نيوتن الثاني، يكون لدينا:

F_net = m a

حيث تبلغ كتلة النظام 19.0 كجم (m = 12.0 كجم + 7.0 كجم) ووجد أن تسارعها يساوي 1.5 متر / ثانية ² في المثال السابق. وهكذا، يكون لدينا:

الآن يمكننا إيجاد القوة المطلوبة:

الدلالة

هذه القوة أقل بكثير من قوة 150 نيوتن التي يبذلها الأستاذ للخلف على الأرض. لا يتم نقل كل قوة 150 نيوتن إلى العربة؛ بعضها يقوم بمهمة تسريع الأستاذ.

يُعد اختيار النظام خطوة تحليلية مهمة سواء في حل المسائل أو في الفهم الشامل لفيزياء الموقف (والتي ليست بالضرورة تكون نفس الأشياء).

تحقق من فهمك: تدريب

كتلتان في حالة سكون وعلى اتصال على سطح عديم الاحتكاك كما هو موضح أدناه، مع m1 = 2.0 كجم، m2 = 6.0 كجم، والقوة المطبقة 24 نيوتن (أ) أوجد تسارع نظام الكتل. (ب) افترض أنه تم فصل الكتل فيما بعد، ما القوة التي ستعطي الكتلة الثانية، التي كتلتها 6.0 كجم، نفس تسارع نظام الكتل؟

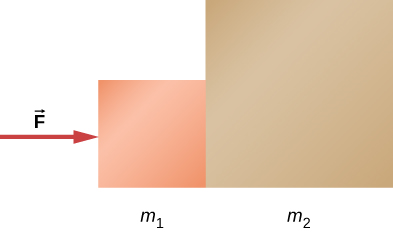
المراجع

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022-2023.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.