بنهاية هذا القسم والمخصص لموضوع عدم اليقين والدقة والضبط في القياس في الكيمياء، سوف تكون قادرًا على:
- تعريف الدقة والضبط في القياسات والتمييز بينهما.
- التمييز بين الأعداد الدقيقة وغير المؤكدة.
- تمثيل عدم اليقين في القياس بشكل صحيح في الكميات باستخدام أرقام ذات دلالة (ذات أهمية).
- تطبيق قواعد التقريب المناسبة للكميات المحسوبة في الكيمياء.
المحتويات
عدم اليقين في القياس
العدّ هو النوع الوحيد من القياس الخالي من عدم اليقين، بشرط ألا يتغير عدد العناصر التي يتم عدها أثناء إجراء عملية العد. نتيجة قياس العد هذا هو مثال على العدد الدقيق. إذا عددنا البيض في كرتونة، فإننا نعرف بالضبط عدد البيض الذي تحتويه الكرتونة. أعداد الكميات المحددة دقيقة أيضًا. بحكم التعريف، 1 قدم هو بالضبط 12 بوصة، 1 بوصة هي بالضبط 2.54 سم، و1 جرام هو بالضبط 0.001 كيلوجرام. الكميات المشتقة من القياسات هي كميات تختلف عن العدّ، ومع ذلك، فهي كميات غير مؤكدة بدرجات متفاوتة بسبب القيود العملية لعملية القياس المستخدمة.
أرقام ذات دلالة (ذات أهمية) في القياس
إن الأعداد التي تعبر عن الكميات المقاسة، على عكس الكميات المحددة أو المحسوبة مباشرة، ليست دقيقة. لقياس حجم السائل في أسطوانة متدرجة، يجب أن تقوم بقراءة التدريج عند قاع العدسة المقعرة للسائل، وهي أدنى نقطة على السطح المنحني للسائل.
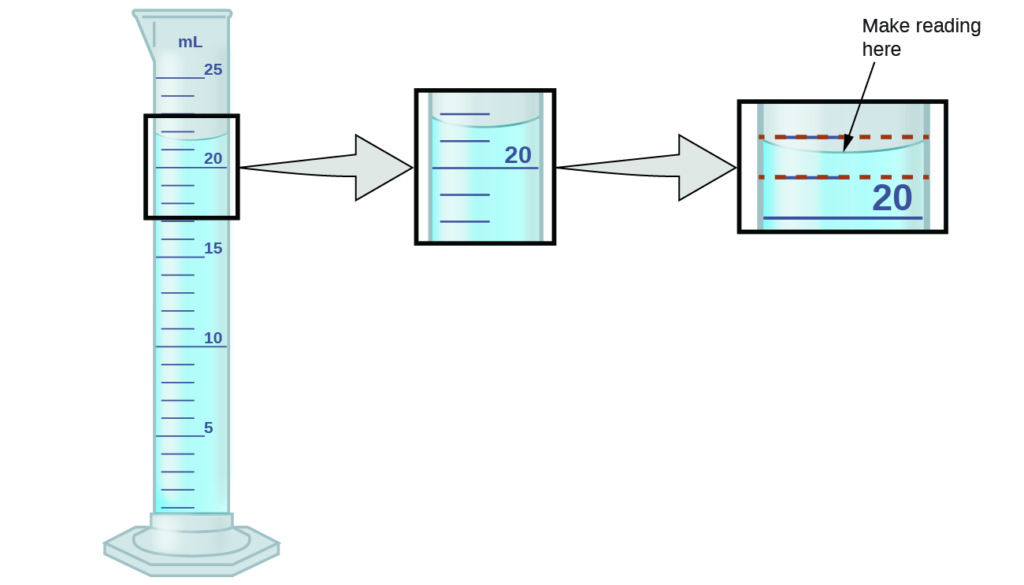
الشكل 1.26: لقياس حجم السائل في هذه الأسطوانة المتدرجة، يجب أن تقسم المسافة بين علامتي 21 و22 مل عقليًا إلى أعشار المليلتر، ثم إجراء قراءة (تقدير) في الجزء السفلي من العدسة المقعرة.
بالرجوع إلى الرسم التوضيحي في الشكل 1.26. يقع الجزء السفلي من التجويف (الذي على شكل عدسة مقعرة) في هذه الحالة بوضوح بين العلامات 21 و22، مما يعني أن حجم السائل بالتأكيد أكبر من 21 مل ولكنه أقل من 22 مل. يبدو أن قعر العدسة أقرب قليلاً إلى علامة 22 مل من علامة 21 مل، وبالتالي فإن التقدير المعقول لحجم السائل سيكون 21.6 مل. في العدد 21.6، إذن، الرقمان 2 و1 هما رقمان مؤكدان Certain، لكن الرقم 6 هو رقم تقديري Estimate. قد يقدّر بعض الأشخاص أن موضع قعر سطح السائل يكون على مسافة متساوية من كل من العلامات ويقدّر الرقم العشري على أنه 5، بينما قد يعتقد البعض الآخر أنه أقرب إلى العلامة 22 مل ويقدّر هذا الرقم ليكون 7.
لاحظ أنه سيكون من غير المجدي محاولة تقدير رقم لمكان الجزء من المئات، بالنظر إلى أن خانة الجزء من العشرات غير مؤكدة. بشكل عام، ستسمح المقاييس الرقمية، مثل المقياس الموجود على هذه الأسطوانة المتدرجة، بالقياسات حتى 1/10 (عُشر) من أصغر تقسيم للمقياس. يحتوي المقياس في هذه الحالة على أقسام سعة 1 مل، وبالتالي يمكن هنا قياس الأحجام إلى أقرب 0.1 مل.
مجالات تطبيق عدم اليقين في القياس
ينطبق هذا المفهوم على جميع القياسات، حتى لو لم تقم بعمل تقدير بشكل فعلي. إذا وضعت ربع دولار على ميزان إلكتروني قياسي، فيمكنك الحصول على قراءة تبلغ 6.72 جم. الرقمان 6 و7 مؤكدان، ويشير الرقم 2 إلى أن كتلة الربع دولار من المحتمل أن تكون بين 6.71 و6.73 جرام. يزن الربع حوالي 6.72 جرام، مع عدم يقين اسمي في القياس مقداره ± 0.01 جرام. إذا قمنا بوزن الربع على ميزان أكثر حساسية، فقد نجد أن كتلته تساوي 6.723 جم. هذا يعني أن كتلته تقع بين 6.722 و6.724 جرامًا، وهي درجة عدم يقين قدرها 0.001 جرام.
كل قياس له البعض من عدم اليقين Uncertainty، والذي يعتمد على الجهاز المستخدم (وقدرة المُستخدم نفسه). جميع الأعداد في القياس، بما في ذلك الرقم أو الخانة الأخيرة غير المؤكدة، تسمى أرقام مهمة أو أرقام ذات دلالة Significant Figures. لاحظ أن الصفر قد يكون قيمة مُقاسة؛ على سبيل المثال، إذا كنت تقف على ميزان يظهر الوزن لأقرب باوند ويظهر “120”، فإن 1 (مئات) و2 (عشرات) والصفر (آحاد) كلها قيم مهمة (مقاسة).
طرق استكشاف الأرقام المهمة
كلما قمت بإجراء القياس بشكل صحيح، فإن جميع الأرقام في النتيجة مهمة. ولكن ماذا لو كنت تحلل قيمة تم التقرير عنها وتحاول تحديد ما هو مهم وما هو غير مهم؟ حسنًا، بالنسبة للمبتدئين، كل الأرقام غير الصفرية مهمة، والأصفار فقط هي التي تتطلب بعض التفكير. سوف نستخدم المصطلحات “الرائدة” Leading و”اللاحقة” Trailing و”المقيّدة” Captive للأصفار وسننظر في كيفية التعامل معها.
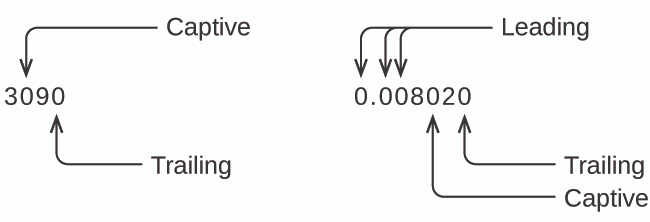
بدءًا من أول رقم غير صفري على اليسار، احسب هذا الرقم وكل الأرقام المتبقية إلى اليمين. هذا هو عدد الأرقام المهمة في القياس ما لم يكن الرقم الأخير عبارة عن صفر زاحف يقع على يسار الفاصلة العشرية.

تنتج الأصفار المقيّدة من القياس وبالتالي فهي دائمًا مهمة. ومع ذلك، فإن الأصفار البادئة ليست ذات دلالة أبدًا – فهي تخبرنا فقط بمكان العلامة العشرية.

الأصفار البادئة في هذا المثال ليست ذات دلالة. يمكننا استخدام التدوين الأسي (كما هو موضح لاحقًا) والتعبير عن الرقم كما يلي: 8.32407 × 10−3؛ ثم يحتوي العدد 8.32407 على جميع الأرقام المهمة، ويحدد 10−3 العلامة العشرية.
عدد الأرقام المهمة غير مؤكد في عدد ينتهي بصفر على يسار موقع الفاصلة العشرية. يمكن أن تكون الأصفار في القياس 1300 جرام مهمة أو يمكن أن تشير ببساطة إلى مكان العلامة العشرية. يمكن حل الغموض باستخدام التدوين الأسي: 1.3 × 10 3 (رقمان مهمان)، 1.30 × 10 3 (ثلاثة أرقام مهمة، إذا تم قياس خانة العشرات)، أو 1.300 × 10 3 (أربعة أرقام مهمة، إذا كانت خانة الآحاد تم قياسها أيضًا). في الحالات التي يكون فيها العدد المنسق عشريًا فقط، من الحكمة افتراض أن جميع الأصفار اللاحقة ليست مهمة (ليست ذات دلالة).
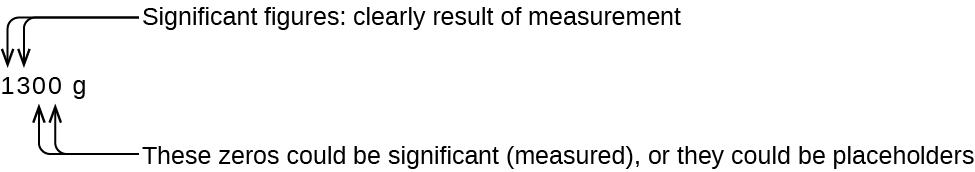
منطق عدم اليقين في القياس
عند تحديد الأرقام المهمة، تأكد من الانتباه إلى القيم المبلغ عنها والتفكير في القياس والأرقام المهمة من حيث ما هو معقول أو محتمل عند تقييم ما إذا كانت القيمة منطقية. على سبيل المثال، أفاد التعداد الرسمي لشهر يناير 2014 أن عدد السكان المقيمين في الولايات المتحدة هو 317،297،725. هل تعتقد أن عدد سكان الولايات المتحدة قد تم تحديده بشكل صحيح وفقًا للأرقام التسعة الهامة المبلغ عنها، أي إلى العدد الدقيق في خانة الآحاد للأشخاص؟ يولد الناس باستمرار أو يموتون أو ينتقلون إلى البلاد أو خارجها، ويتم وضع افتراضات لحساب العدد الكبير من الأشخاص الذين لم يتم احتسابهم في الواقع. بسبب حالات عدم اليقين هذه، قد يكون من المعقول توقع أننا نعرف عدد السكان ربما في حدود مليون أو نحو ذلك، وفي هذه الحالة يجب الإبلاغ عن عدد السكان على أنه 3.17 × 10 8 شخص.
الأرقام المهمة (ذات دلالة) في الحسابات
المبدأ الثاني المهم لعدم اليقين هو أن النتائج المحسوبة من القياس تكون على الأقل غير مؤكدة مثل القياس نفسه. يجب أن نأخذ عدم اليقين في قياساتنا في الاعتبار لتجنب تحريف عدم اليقين في النتائج المحسوبة. تتمثل إحدى طرق القيام بذلك في الإبلاغ عن نتيجة عملية حسابية بالعدد الصحيح للأرقام المهمة، والتي يتم تحديدها من خلال القواعد الثلاثة التالية لتقريب الأعداد:
- عندما نجمع أو نطرح أعدادًا، يجب تقريب النتيجة إلى نفس عدد المنازل العشرية مثل العدد الذي يحتوي على أقل عدد من المنازل العشرية (أقل قيمة دقيقة من حيث الجمع والطرح).
- عندما نضرب أو نقسم الأعداد، يجب أن نقرب النتيجة إلى نفس عدد الخانات مثل الرقم الذي يحتوي على أقل عدد من الأرقام المهمة (أقل قيمة دقيقة من حيث الضرب والقسمة).
- إذا كان الرقم المطلوب إسقاطه (الرقم الموجود مباشرة على يمين الرقم المطلوب الاحتفاظ به) أقل من 5، فإننا “نقرب لأسفل” ونترك الرقم المحتفظ به دون تغيير؛ إذا كان العدد أكبر من 5، فإننا “نقرب” ونزيد الرقم المحتفظ به بمقدار 1؛ وإذا كان الرقم المسقط هو 5، فإننا نقرب لأعلى أو لأسفل، أيهما ينتج قيمة زوجية للرقم المحتفظ به. (قد يبدو لك الجزء الأخير من هذه القاعدة غريبًا بعض الشيء، لكنه يعتمد على إحصائيات موثوقة ويهدف إلى تجنب أي تحيز عند إسقاط الرقم “5”، نظرًا لأنه قريب بنفس القدر من القيم المحتملة للرقم المحتفظ به).
توضح الأمثلة التالية تطبيق هذه القاعدة في تقريب عدد قليل من الأعداد المختلفة إلى ثلاثة أرقام مهمة:
- 0.028675 تقريب “لأعلى” إلى 0.0287 (الرقم المسقط، 7، وهو أكبر من 5)
- تقريب 18.3384 “لأسفل” إلى 18.3 (الرقم المسقط، 3، وهو أقل من 5)
- تقريب 6.8752 “لأعلى” إلى 6.88 (الرقم المسقط هو 5، والرقم المحتفظ به أصبح زوجي)
- 92.85 تقريب “لأسفل” إلى 92.8 (الرقم المسقط هو 5، والرقم المحتفظ به أصبح زوجي)
أمثلة على عدم اليقين في القياس وطرق التقريب
دعونا نعمل من خلال هذه القواعد مع بعض الأمثلة.
مثال 1.3: تقريب الأعداد
قرِّب ما يلي إلى العدد المحدد من الأرقام المهمة:
- (أ) 31.57 (إلى رقمين مهمين)
- (ب) 8.1649 (حتى ثلاثة أرقام مهمة)
- (ج) 0.051065 (لأربعة أرقام مهمة)
- (د) 0.90275 (حتى أربعة أرقام مهمة)
الحل
- (أ) 31.57 تقريب “لأعلى” إلى 32 (الرقم المسقط هو 5، والرقم المحتفظ به يصبح زوجي)
- (ب) يتم تقريب 8.1649 “لأسفل” إلى 8.16 (الرقم المسقط، 4، أقل من 5)
- (ج) 0.051065 تقرب “لأسفل” إلى 0.05106 (الرقم المسقط هو 5، والرقم المحتفظ به يصبح زوجي)
- (د) تقريب 0.90275 “لأعلى” إلى 0.9028 (الرقم المسقط هو 5، والرقم المحتفظ به يصبح زوجي)
تحقق من فهمك
قرِّب ما يلي إلى العدد المحدد من الأرقام المهمة:
- (أ) 0.424 (حتى رقمين مهمين)
- (ب) 0.0038661 (حتى ثلاثة أرقام مهمة)
- (ج) 421.25 (حتى أربعة أرقام مهمة)
- (د) 28683.5 (إلى خمسة أرقام مهمة)
الحل: (أ) 0.42؛ (ب) 0.00387؛ (ج) 421.2؛ (د) 28684
مثال 1.4: الجمع والطرح بأرقام مهمة (ذات دلالة)
القاعدة: عندما نجمع أو نطرح أعدادًا، يجب تقريب النتيجة إلى نفس عدد المنازل العشرية مثل العدد الذي يحتوي على أقل عدد من المنازل العشرية (أي أقل قيمة دقيقة من حيث الجمع والطرح).
- (أ) اجمع 1.0023 جم و4.383 جم.
- (ب) اطرح 421.23 جم من 486 جم.
الحل
(أ)
1.0023 جرام
+ 4.383 جرام
5.3853 جرام
الإجابة هي 5.385 جم (تقريبًا إلى خانة الألف، ثلاث منازل عشرية).
(ب)
486 جرام
– 421.23 جم
64.77 جرام
الإجابة 65 جم (تقريب إلى خانة الآحاد، بدون منازل عشرية).

تحقق من فهمك
- (أ) أضف 2.334 مل و0.31 مل.
- (ب) اطرح 55.8752 م من 56.533 م.
- الجواب: (أ) 2.64 مل؛ (ب) 0.658 م.
مثال 1.5: الضرب والقسمة بأرقام ذات دلالة
القاعدة: عندما نضرب الأعداد أو نقسمها، يجب أن نقرب النتيجة إلى نفس عدد الأرقام مثل العدد الذي يحتوي على أقل عدد من الأرقام المعنوية (أقل قيمة دقيقة من حيث الضرب والقسمة).
- (أ) اضرب 0.6238 سم في 6.6 سم.
- (ب) قسّم 421.23 جم على 486 مل.
الحل
(أ) 0.6238 سم × 6.6 سم = 4.11708 سم 2 = النتيجة 4.1 سم 2 (تقريبًا إلى رقمين مهمين).
أربعة أرقام مهمة × اثنين من الأرقام المهمة، يعطي إجابة اثنين من الأرقام المهمة (ذات دلالة).
(ب) 421.23 جرام / 486 مل = 0.86728 جم / مل = النتيجة 0.867 جم / مل (ثلاثة أرقام مهمة).
رقمين مهمين / ثلاثة أرقام مهمة، يعطي إجابة ثلاثة أرقام مهمة.
تحقق من فهمك
- (أ) اضرب 2.334 سم و0.320 سم.
- (ب) قسّم 55.8752 مترًا على 56.53 ثانية.
الجواب: (أ) 0.747 سم 2 (ب) 0.9884 م / ث
في خضم كل هذه الجوانب الفنية، من المهم أن تضع في اعتبارك سبب استخدامنا للأرقام المهمة (ذات الدلالة) وقواعد التقريب هو من أجل تمثيل اليقين للقيم التي نبلغ عنها بشكل صحيح ولضمان عدم تمثيل النتيجة المحسوبة على أنها أكثر يقينًا من أقل قيمة معينة مستخدمة في الحساب.
مثال 1.6: إجراء الحساب بأرقام مهمة
يبلغ طول أحد الأحواض الشائعة 13.44 ديسيمترًا، وعرضه 5.920 ديسيمترًا، وعمقه 2.54 ديسيمترًا. افترض أن الحوض مستطيل واحسب حجمه التقريبي باللترات.
الحل
الحجم = الطول × العرض × الارتفاع
بالتعويض عن القيم المُعطاة، ينتج لنا:
الحجم = 13.44 دسم × 5.920 دسم × 2.54 دسم
= 202.09459 … دسم 3 (قيمة من الآلة الحاسبة)
= 202 دسم 3 ، أو 202.1 دسم 3 (تم تقريب الإجابة إلى ثلاثة أرقام مهمة).
تحقق من فهمك
ما كثافة سائل كتلته 31.1415 جم وحجمه 30.13 سم 3؟
الجواب: 1.034 جم / مل
مثال 1.7: التحديد التجريبي للكثافة باستخدام إزاحة الماء
يتم وزن قطعة من حديد التسليح ثم غمرها في أسطوانة مدرجة مملوءة جزئيًا بالماء، مع النتائج كما هو موضح بالشكل التالي.
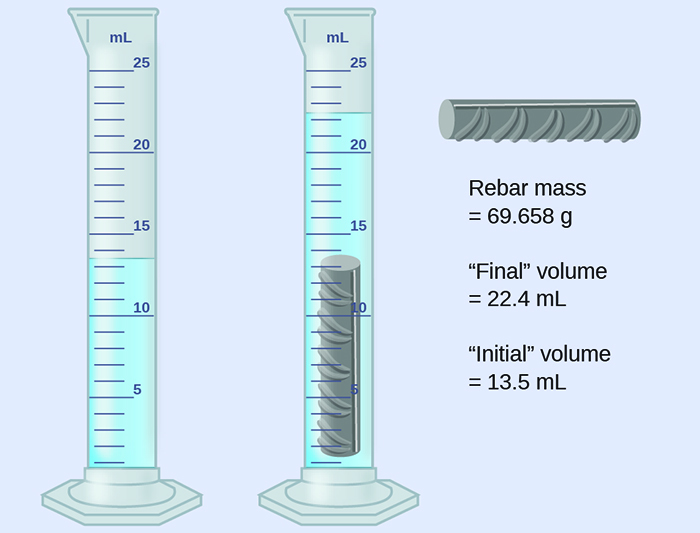
- (أ) استخدم هذه القيم لتحديد كثافة قطعة حديد التسليح هذه.
- (ب) يتكون حديد التسليح في الغالب من الحديد. هل نتيجتك في (أ) تدعم هذا البيان؟ كيف؟
الحل
حجم قطعة حديد التسليح يساوي حجم الماء المُزاح:
الحجم = 22.4 مل – 13.5 مل = 8.9 مل = 8.9 سم 3 (مقربًا إلى أقرب 0.1 مل، وفقًا لقاعدة الجمع والطرح مع الأرقام المهمة).
الكثافة هي نسبة الكتلة إلى الحجم:
الكثافة = الكتلة / الحجم = 69.658 جم / 8.9 سم 3 = 7.8 جم / سم 3 (مقربًا لأقرب رقمين معنويين مهمين، وفقًا لقاعدة الضرب والقسمة مع الأرقام المهمة).
من الجدول 1.4 ، تبلغ كثافة الحديد 7.9 جم / سم 3، وهي قريبة جدًا من كثافة حديد التسليح، مما يقدم بعض الدعم لحقيقة أن حديد التسليح يتكون في الغالب من الحديد.
تحقق من فهمك:
يتم وزن قطعة غير منتظمة الشكل من مادة صفراء لامعة ثم تُغمر في أسطوانة مدرّجة، مع النتائج كما هو موضح بالشكل التالي:

(أ) استخدم هذه القيم لتحديد كثافة هذه المادة.
(ب) هل لديك أي تخمينات معقولة فيما يتعلق بهوية هذه المادة؟ اشرح أسبابك.
الحل
(أ) 19 جم / سم 3؛ (ب) من المحتمل أن يكون ذهبًا؛ المظهر متوافق مع الذهب وقريب جدًا من الكثافة المعطاة للذهب في الجدول 1.4.
الدقة والضبط في القياس
عادةً ما يقوم العلماء بإجراء قياسات متكررة للكمية لضمان جودة نتائجهم ولمعرفة كل من الدقة Accuracy والضبط Precision لنتائجهم. يُقال أن القياسات مضبوطة أو مُحكمة Precise إذا كانت تؤدي إلى نتائج متشابهة جدًا عند تكرارها بنفس الطريقة. يعتبر القياس دقيقًا Accurate إذا أسفر عن نتيجة قريبة جدًا من القيمة الحقيقية أو المقبولة. تتفق القيم المضبوطة مع بعضها البعض؛ تتفق القيم الدقيقة مع القيمة الحقيقية. يمكن أن تمتد هذه التوصيفات إلى سياقات أخرى، مثل نتائج مسابقة الرماية كما في (الشكل 1.27).
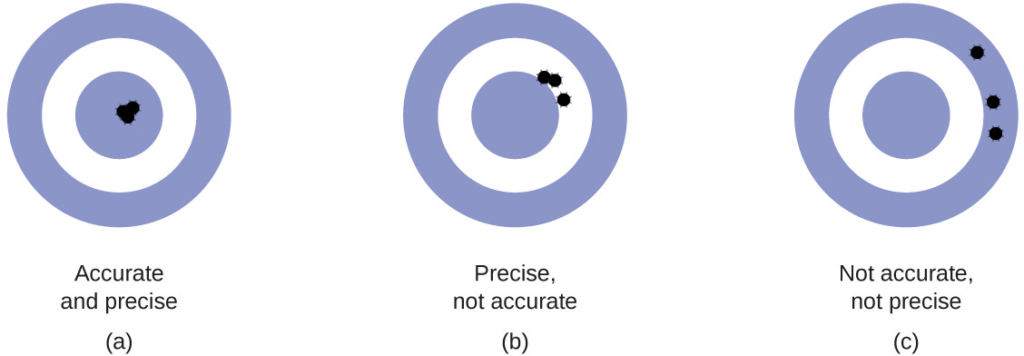
الشكل 1.27 (أ) هذه الأسهم قريبة من الهدف وقريبة من بعضها البعض، لذا فإنها دقيقة ومضبوطة. (ب) هذه الأسهم قريبة من بعضها البعض ولكنها ليست على الهدف، لذا فهي مضبوطة ولكنها غير دقيقة. (ج) هذه الأسهم ليست على الهدف وليست قريبة من بعضها البعض، لذا فهي ليست دقيقة ولا مضبوطة.
مثال تطبيقي للتمييز بين الدقة والضبط
لنفترض أن كيميائيًا متخصصًا في مراقبة الجودة في شركة أدوية مكلف بفحص دقة وإحكام ثلاث آلات مختلفة تهدف إلى تسليم 10 أونصات (296 مل) من شراب السعال في زجاجات التخزين. تشرع في استخدام كل آلة لملء خمس زجاجات ثم تحدد بعناية الحجم الفعلي الذي تم تسليمه، وقامت بالحصول على النتائج المدرجة في الجدول 1.5.
| موزع 3 | موزع 2 | موزع 1 |
| 296.1 | 298.3 | 283.3 |
| 295.9 | 294.2 | 284.1 |
| 296.1 | 296.0 | 283.9 |
| 296.0 | 297.8 | 284.0 |
| 296.1 | 293.9 | 284.1 |
بالنظر إلى هذه النتائج، سيبلغ الكيميائي أن الموزع رقم 1 مضبوط Precise (جميع القيم قريبة من بعضها البعض، في حدود بضعة أعشار من المليلتر) ولكنها ليست دقيقة Not Accurate (لا توجد أي من القيم قريبة من القيمة المستهدفة البالغة 296 مل، كل منها أكبر ولكن بقيم أقل من 10 مل). تمثل نتائج الموزع رقم 2 دقة محسّنة Improved Accuracy (كل حجم أقل بقيمة 3 مل من القيمة المستهدفة 296 مل) ولكن بإحكام أسوأ Worse Precision (تختلف الأحجام بأكثر من 4 مل). أخيرًا، يمكنه الإبلاغ عن أن الموزع رقم 3 يعمل بشكل جيد، ويوزع شراب السعال على حد سواء بدقة Accuracy (جميع الأحجام تبعد في حدود 0.1 مل من الحجم المستهدف) وبإحكام Precisely (تختلف الأحجام عن بعضها البعض بما لا يزيد عن 0.2 مل).
المراجع
- مقرر الكيمياء، كلية OpenStax، تاريخ النشر OpenStax College, Chemistry ،11 March 2015. الفصل الأول، الأفكار والمفاهيم الأساسية في الكيمياء.
- موسوعة الكيمياء من الألف إلى الياء، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022-2023.