استخدام النموذج الخطي العام أحادي المتغير لإجراء تحليل التباين الثنائي
قامت سلسلة متاجر بقالة بمسح مجموعة من العملاء فيما يتعلق بعاداتهم الشرائية. بالنظر إلى نتائج الاستطلاع ومقدار ما أنفقه كل عميل في الشهر السابق، يريد المتجر معرفة ما إذا كان تكرار التسوق للعملاء مرتبطًا بالمبلغ الذي ينفقونه في الشهر، مع التحكم في جنس العميل. من أجل ذلك يتم استخدام إجراء النموذج الخطي العام أحادي المتغير لإجراء تحليل التباين الثنائي.
يتم جمع المعلومات في grocery_1month.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات. استخدم لنموذج الخطي العام أحادي المتغير لإجراء تحليل التباين الثنائي Tow-Factor ANOVA (أو ثنائي الاتجاه Tow-Way ANOVA) على المبالغ التي يتم إنفاقها.
إجراء تحليل التباين الثنائي
لإجراء تحليل النموذج الخطي العام أحادي المتغير GLM Univariate:
1. اختر من القوائم: تحليل> النموذج الخطي العام > أحادي المتغير …
Analyze > General Linear Model > Univariate…
يظهر مربع حوار النموذج الخطي العام أحادي المتغير GLM Univariate، وفيه سوف يتم تحديد المبلغ الذي تم إنفاقه كمتغير تابع ونوع الجنس ونمط التسوق كعوامل ثابتة، وذلك كما يلي:
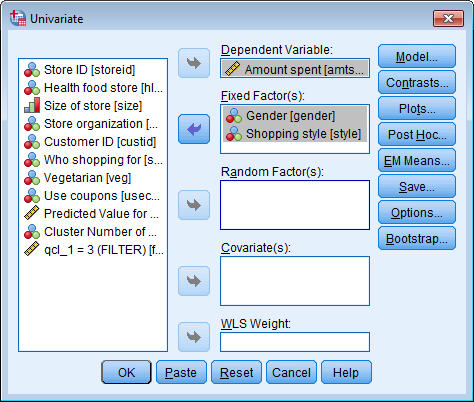
2. حدد المبلغ الذي تم إنفاقه Amount spent كمتغير تابع dependent variable.
3. حدد الجنس Gender وأسلوب التسوق Shopping style كعاملين ثابتين fixed factors.
4. انقر فوق التخطيطات Plots.
يظهر مربع حوار التخطيط Plot كما يلي:
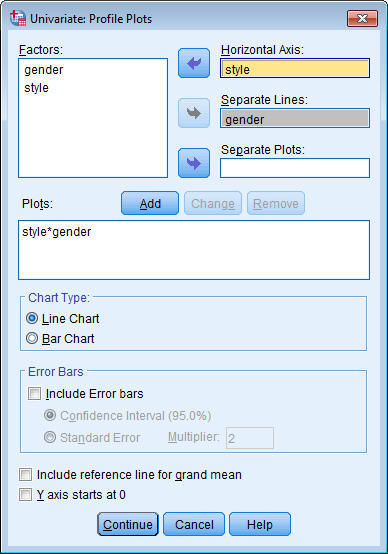
5. حدد النمط style كمتغير المحور الأفقي horizontal axis.
لاحظ أنه لا يتم عرض تسميات المتغير في مربعات الحوار الفرعية للنموذج الخطي العام أحادي المتغير GLM Univariate.
6. حدد الجنس gender كمتغير سطور منفصلة separate lines.
7. انقر فوق إضافة Add.
8. انقر فوق متابعة Continue.
تحديد المقارنات المتعددة
9. انقر فوق المقارنات المتعددة البَعدية Post Hoc في مربع حوار النموذج الخطي العام أحادي المتغير GLM Univariate.
يظهر مربع حوار المقارنات المتعددة البَعدية Post Hoc كما يلي:
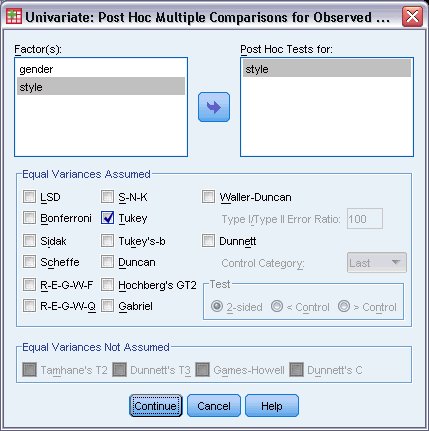
10. حدد النمط style باعتباره المتغير الذي يجب إنتاج الاختبارات اللاحقة (أو البَعدية) له.
11. حدد Tukey في مجموعة “التباينات المتساوية المفترضة” Equal Variances Assumed.
12. انقر فوق متابعة Continue.
13. انقر فوق خيارات Options في مربع حوار النموذج الخطي العام أحادي المتغير.
يظهر مربع حوار الخيارات كما يلي:
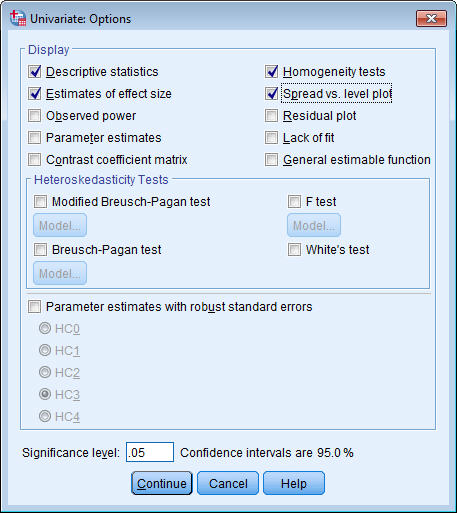
14. حدد “الجنس * النمط” gender*style باعتباره المصطلح الذي يجب عرض المتوسطات من أجله في مجموعة العرض Display.
15. حدد الإحصائيات الوصفية Descriptive statistics، واختبارات التجانس Homogeneity tests، وتقديرات حجم التأثير Estimates of effect size، ومخطط الانتشار مقابل المستوى Spread vs. level plot في مجموعة العرض Display.
16. انقر فوق متابعة Continue.
17. انقر فوق “موافق” OK في مربع الحوار أحادي المتغير GLM.
الإحصائيات الوصفية
الشكل التالي يبين نتائج الإحصائيات الوصفية Descriptive Statistics:
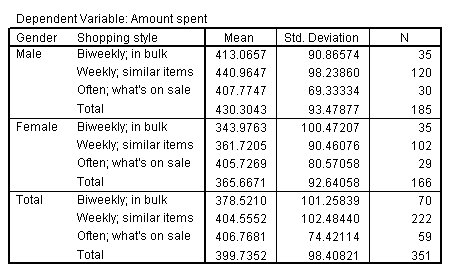
يعرض هذا الجدول الإحصائيات الوصفية لكل مجموعة من العوامل في النموذج model.
يبدو أن هناك تأثيرًا لأسلوب التسوق Shopping style؛ في المتوسط، ينفق العملاء الذين يترددون على موقع التسوق “كل أسبوعين” biweekly مبلغًا قدره 378.52 دولارًا أمريكيًا، بينما ينفق العملاء الذين يترددون على موقع التسوق “كل أسبوع” weekly مبلغًا قدره 404.55 دولارًا أمريكيًا، وينفق العملاء الذين يترددون “غالبًا” على موقع التسوق often مبلغًا قدره 406.76 دولارًا أمريكيًا. يبدو أيضًا أن هناك تأثيرًا لنوع الجنس Gender effect؛ في المتوسط، ينفق الذكور في العينة 430.30 دولارًا أمريكيًا مقارنة بـ 365.66 دولارًا للإناث. أخيرًا، قد يكون هناك تأثير تفاعلي بين الجنس Gender وأسلوب التسوق Shopping style، لأن متوسط الفروق في المبلغ الذي يتم إنفاقه حسب أسلوب التسوق يختلف بين الجنسين. على سبيل المثال، يميل العملاء الذكور “كل أسبوعين” إلى إنفاق أكثر من العملاء الذكور الذين يترددون “غالبًا” على مركز التسوق، ولكن هذا الاتجاه ينعكس بالنسبة للعملاء الإناث الذين يترددون “كل أسبوعين” و”غالبًا” على موقع التسوق .
يوضح العمود N في الجدول وجود أحجام خلايا غير متساوية. يفضل معظم العملاء الذين يتسوقون على أساس أسبوعي. تبدو الانحرافات المعيارية standard deviations متجانسة نسبيًا، وبالرغم من ذلك، يجب عليك التحقق من اختبار ليفين Levene’s test ومخططات الانتشار مقابل المستوى spread-versus-level plots للتأكد.
اختبار تجانس التباين
الشكل التالي يبين نتيجة اختبار ليفين لتكافؤ تباينات الخطأ error variances:

يختبر هذا الجدول الفرضية الصفرية القائلة بأن تباين مصطلح الخطأ ثابت عبر الخلايا المحددة بواسطة مجموعة مستويات العامل factor levels. نظرًا لأن قيمة أهمية الاختبار، 0.330، هي أكبر من 0.10، فلا يوجد سبب للاعتقاد بانتهاك افتراض الفروق المتساوية. وبالتالي، فإن الاختلافات الصغيرة في الانحرافات المعيارية للمجموعة group standard deviations التي لوحظت في جدول الإحصاء الوصفي ترجع إلى التباين العشوائي random variation.
مخطط الانتشار مقابل المستوى
الشكل التالي يبين مخطط الانتشار مقابل المستوى spread-versus-level plots:
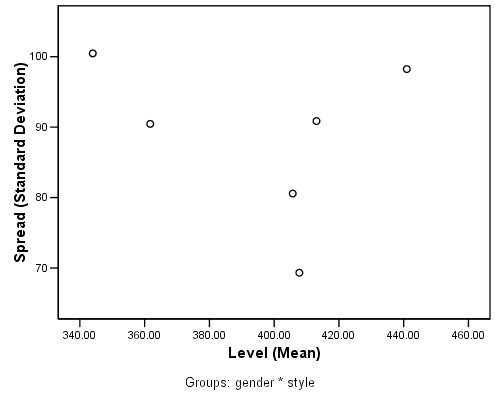
مخطط الانتشار مقابل المستوى هو مخطط مبعثر scatterplot لمتوسطات الخلية cell means والانحرافات المعيارية standard deviations في جدول الإحصاء الوصفي. وهو يوفر اختبارًا مرئيًا لافتراض التباينات المتساوية، مع فائدة إضافية تتمثل في مساعدتك في تقييم ما إذا كانت انتهاكات الافتراض ترجع إلى علاقة بين متوسطات الخلية والانحرافات المعيارية. لا يوجد نمط واضح في هذا المخطط، لذلك لا يوجد ما يشير إلى مثل هذه العلاقة هنا.
الاختبارات البَعدية أو اللاحقة
الشكل التالي يبين نتائج المقارنات المتعددة البَعدية Post Hoc:
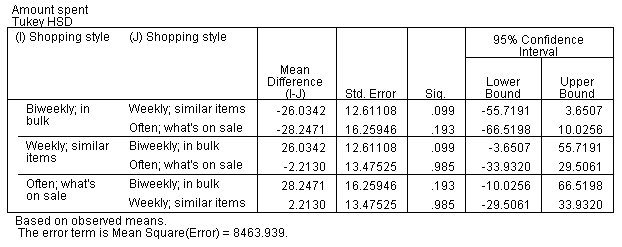
تساعدك اختبارات التأثيرات بين الموضوعات على تحديد أهمية العامل. ومع ذلك، فهي لا تشير إلى كيفية اختلاف مستويات العامل. تُظهر الاختبارات البَعدية (أو اللاحقة) الاختلافات في المتوسطات المتوقعة Mean Difference من خلال النموذج لكل زوج من مستويات العوامل.
يعرض العمود الأول الاختبارات البَعدية المختلفة. يعرض العمودين التاليين زوج مستويات العوامل التي يتم اختبارها. عندما تكون قيمة الأهمية للفرق في المبلغ الذي يتم إنفاقه لزوج من مستويات العوامل أقل من 0.05، تتم طباعة علامة النجمة (*) بواسطة الفرق. في هذه الحالة، لا يبدو أن هناك فروقًا ذات دلالة إحصائية في عادات الإنفاق للعملاء “كل أسبوعين” biweekly أو “كل أسبوع” weekly أو “غالبًا” often.
المجموعات الفرعية المتجانسة
الشكل التالي يبين المجموعات الفرعية المتجانسة Homogenous subsets:
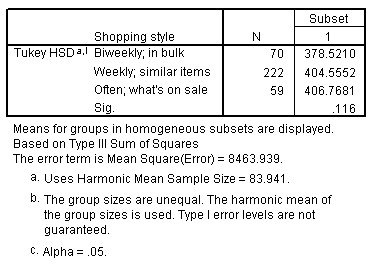
يأخذ جدول المجموعات الفرعية المتجانسة نتائج الاختبارات البَعدية (اللاحقة) ويظهرها في شكل يسهل تفسيره. في أعمدة المجموعة الفرعية، يتم عرض مستويات العوامل التي ليس لها تأثيرات مختلفة بشكل ملحوظ في نفس العمود. في هذا المثال، تحتوي المجموعة الفرعية الأولى على عملاء “كل أسبوعين” و “أسبوعيًا” و “غالبًا”. هؤلاء هم جميع العملاء، لذلك لا توجد مجموعات فرعية أخرى.
تشير الاختبارات البَعدية إلى أن الجهود المبذولة لإغراء العملاء بالتسوق أكثر من المعتاد تُهدر لأنهم لن ينفقوا أكثر بكثير. ومع ذلك، فإن نتائج الاختبار اللاحق لا تأخذ في الحسبان مستويات العوامل الأخرى، وبالتالي تتجاهل إمكانية وجود تأثير التفاعل مع الجنس الذي يظهر في جدول الإحصاء الوصفي. انظر إلى المتوسطات الهامشية المقدرة estimated marginal means لترى كيف يمكن لهذا أن يغير استنتاجاتك.
المتوسطات الهامشية المقدرة
الشكل التالي يبين المتوسطات الهامشية المقدرة Estimated Marginal Means:
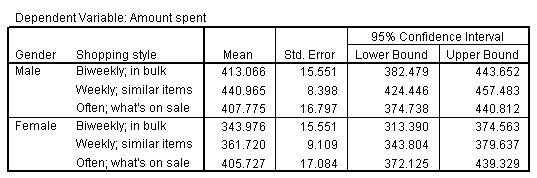
يعرض هذا الجدول المتوسطات الهامشية المقدرة بالنموذج والأخطاء القياسية Standard Errors للمبلغ الذي تم إنفاقه Amount spent بالنسبة لتركيبات العوامل من الجنس Gender وأسلوب التسوق Shopping style. هذا الجدول مفيد لاستكشاف تأثير التفاعل المحتمل بين هذين العاملين.
في هذا المثال، من المتوقع أن ينفق العميل الذكر الذي يقوم بعمليات شراء “كل أسبوع” weekly حوالي 440.96 دولارًا أمريكيًا، بينما من المتوقع أن ينفق العميل الذي يقوم بعمليات الشراء “غالبًا” often حوالي 407.77 دولارًا أمريكيًا. من المتوقع أن تنفق الزبونة التي تقوم بعمليات شراء “كل أسبوع” weekly حوالي 361.72 دولارًا أمريكيًا، بينما من المتوقع أن تنفق الزبونة التي تقوم بعمليات الشراء “غالبًا” often حوالي 405.72 دولارًا أمريكيًا. وبالتالي، هناك فرق بين العملاء الذين يترددون على مركز التسوق “الأسبوعيين” و”غالبًا”، اعتمادًا على جنس العميل.
تشير هذه الحقيقة إلى وجود تأثير تفاعل بين الجنس وأسلوب التسوق. إذا لم يكن هناك تفاعل، فستتوقع أن يظل الفرق بين أنماط التسوق ثابتًا للعملاء من الذكور والإناث. يمكن رؤية التفاعل بسهولة أكبر في مخططات البروفايل الملف الشخصي Profile plot.
مخطط الملف الشخصي
الشكل التالي يبين مخطط الملف الشخصي Profile plot:
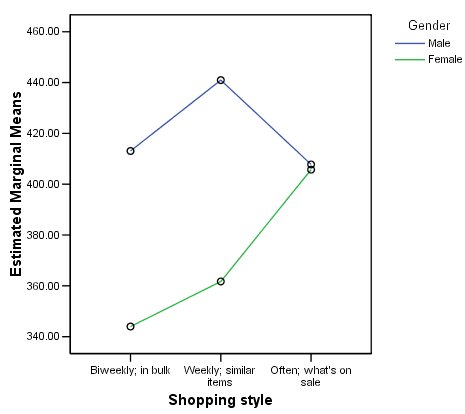
مخطط الملف الشخصي Profile plot هو تمثيل مرئي لجدول المتوسطات الهامشية. تظهر مستويات عوامل نمط التسوق على طول المحور الأفقي. يتم إنتاج خطوط منفصلة لكل مستوى من مستويات الجنس.
وبالتناوب، يمكن عرض مستويات عامل الجنس على طول المحور الأفقي، مع إنشاء خطوط منفصلة لكل مستوى من أنماط التسوق.
إذا لم يكن هناك تأثير تفاعل، فستكون الخطوط الموجودة في الجدول متوازية. بدلاً من ذلك، يمكنك أن ترى أن الفرق في الإنفاق بين العملاء الذين يترددون “كل أسبوع” و”غالبًا” يكون أكبر بالنسبة للعملاء الإناث، حيث ينحدر خط العملاء الذكور إلى أسفل بينما ينحدر خط العملاء من الإناث إلى أعلى. هذا تأثير تفاعل قوي ومن غير المحتمل أن يكون بسبب الصدفة، ولكن يجب عليك التحقق من اختبارات التأثيرات بين الموضوعات tests of between-subjects effects لتأكيد أهميتها.
اختبارات التأثيرات بين الموضوعات
الشكل التالي يبين نتيجة اختبارات التأثيرات بين الموضوعات tests of between-subjects effects:
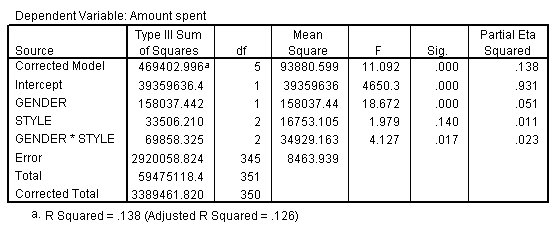
هذا هو تحليل جدول التباين. يتم اختبار كل مصطلح term في النموذج، بالإضافة إلى النموذج ككل، لقدرته على حساب التباين في المتغير التابع. لاحظ أنه لا يتم عرض تسميات المتغيرات في هذا الجدول. قيمة الأهمية لكل مصطلح term، باستثناء النمط STYLE، أقل من 0.05. لذلك فإن كل مصطلح، باستثناء النمط STYLE، له دلالة إحصائية.
يوضح إحصاء مربع إيتا الجزئي Partial Eta Squared الأهمية “العملية” لكل مصطلح، استنادًا إلى نسبة التباين (مجموع المربعات) المحسوبة بالمصطلح إلى مجموع التباين sum of the variation، المحسوب بدوره بنسبة المصطلح والتباين إلى الخطأ . تشير القيم الأكبر لمربع إيتا الجزئي Partial Eta Squared إلى قدر أكبر من التباين المحسوب لمصطلح النموذج، بحد أقصى 1. هنا المصطلحات الفردية، بالرغم من وجود دلالة إحصائية لها، إلا أنها ليس لها تأثير كبير على قيمة المبلغ الذي تم إنفاقه Amount spent.
ملخص تحليل التباين الثنائي باستخدام GLM Univariate
في هذا المثال، لم تكشف الاختبارات البَعدية (أو اللاحقة) عن اختلاف في الإنفاق بين العملاء الذين يتسوقون كل أسبوعين وأولئك الذين يتسوقون غالبَا. ومع ذلك، كشفت المتوسطات الهامشية المقدرة ومخططات الملف الشخصي عن تفاعل بين العاملين، مما يشير إلى أن العملاء الذكور الذين يتسوقون مرة واحدة في الأسبوع يكونون أكثر ربحية من أولئك الذين يتسوقون غالبًا. بينما ينعكس النمط بالنسبة للعملاء الإناث. تم تأكيد أهمية تأثير التفاعل هذا من خلال نتائج جدول تحليل التباين الثنائي Tow-Factor ANOVA (أو تحليل التباين ثنائي الاتجاه Tow-Way ANOVA).
المصدر
- كتاب التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، تركيا، 2022.
- الموقع الرسمي لشركة IBM ® برنامج SPSS