المقارنات المتعددة بين المتوسطات
تعد التباينات Contrasts طريقة فعالة وقوية لمقارنة المجموعات التي تريد مقارنتها بشكل محدد ودقيق، باستخدام أي أوزان للتباين التي تحتاجها. ومع ذلك، هناك أوقات لا يوجد فيها أو لا تحتاج إلى مثل هذه المقارنات المحددة. يسمح لك إجراء تحليل التباين أحادي الاتجاه One-Way ANOVA بمقارنة كل متوسط مجموعة من المجموعات مع بعضها البعض، وهي طريقة تُعرف باسم المقارنات المتعددة الزوجية بين المتوسطات Pairwise Multiple Comparisons.
قام مدير مبيعات بتحليل بيانات التدريب باستخدام تحليل التباين الأحادي One-Way ANOVA. وبالرغم من أنه تم العثور على اختلافات كبيرة في المجموعة، إلاّ أنه لا توجد فرضيات سابقة حول كيفية اختلاف المجموعات الثلاث. لذلك، قرر ببساطة مقارنة كل مجموعة بالمجموعة الأخرى بطريقة المقارنات المتعددة.
يستخدم هذا المثال الملف salesperformance.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات.
إجراء تحليل المقارنات المتعددة
1. لبدء التحليل، اختر من القوائم: تحليل> مقارنة المتوسطات > تحليل التباين أحادي الاتجاه …
Analyze > Compare Means > One-Way ANOVA…
يظهر مربع حوار تحليل التباين أحادي الاتجاه، والبدء بتحديد المتغير التابع والمتغير العاملي كما يلي:
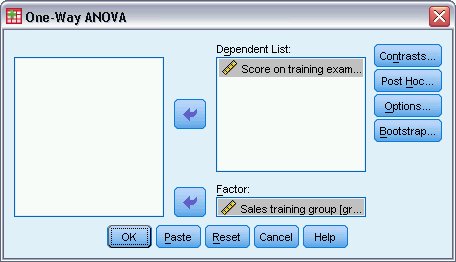
2. حدد الدرجة في امتحان التدريب Score on training exam كمتغير تابع dependent variable.
3. حدد مجموعة تدريب المبيعات Sales training group كمتغير عاملي factor variable.
4. انقر فوق الاختبارات أو المقارنات المتعددة البَعدية Post Hoc.
تنقسم الاختبارات البَعدية Post Hoc إلى مجموعتين:
- المجموعة الأولى تفترض مجموعات ذات تباينات متساوية.
- المجموعة الثانية لا تفترض أن التباينات أو الفروق متساوية. نظرًا لأن اختبار Levene قد أثبت بالفعل أن الفروق بين مجموعات التدريب مختلفة بشكل كبير، فإننا نختاره من هذه القائمة. (راجع موضوع تحليل التباين أحادي الاتجاه).
5. حدد Tamhane’s T2.
6. انقر فوق متابعة أو Continue.
7. انقر فوق “موافق” أو OK في مربع حوار تحليل التباين أحادي الاتجاه.
جدول الاختبار البَعدي أو اللاحق
- كان أداء مجموعة المتدربين الذين حصلوا على يوم تدريب واحد فقط أقل بكثير من المجموعات الأخرى.
- لا يختلف المتدربون الذين لديهم يومين وثلاثة أيام من التدريب إحصائيًا في متوسطات الأداء. على الرغم من هذه المساواة، لا يزال بإمكان المدير النظر في الميزة الإضافية ليوم التدريب الثالث، نظرًا للانخفاض الكبير في التباين.
خلاصة موضوع تحليل التباين أحادي الاتجاه
باستخدام إجراء تحليل التباين أحادي الاتجاه One-Way ANOVA، يمكنك:
- التحقق من صحة افتراض المساواة في التباين
- الحصول على جدول ANOVA والنتائج
- تفقد متوسطات المجموعة بصريًا
- إجراء تحليلات تباين مخصصة، مصممة وفقًا لفرضياتك المحددة
- المقارنات المتعددة بين كل متوسط مع المتوسطات الأخرى، بافتراض المساواة في التباين أم لا
- إجراء نوعين من التحليل القوي للتباين
الإجراءات ذات الصلة
يستخدم إجراء تحليل التباين أحادي الاتجاه One-Way ANOVA لاختبار الفرضية القائلة بأن متوسطات عدة عينات متساوية.
يمكنك استخدام إجراء المتوسطات Means بالتناوب للحصول على تحليل أحادي الاتجاه للتباين مع اختبار للخطية.
إذا كانت لديك عوامل متعددة، فاستخدم إجراء النموذج الخطي العام أحادي المتغير التابع General Linear Model Univariate والذي يُرمز له بالاختصار GLM Univariate، للحصول على تحليل ثنائي الاتجاه للتباين، وتحليل التغاير Covariance، والمزيد.
المصدر
- كتاب التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، تركيا، 2022.
- الموقع الرسمي لشركة IBM ® برنامج SPSS