المتجهات – الكميات القياسية والكميات المتجهة

المتجهات – الكميات القياسية والكميات المتجهة

تعطي اللافتات على الطريق معلومات حول المسافات والاتجاهات إلى المدن أو إلى المواقع الأخرى المتعلقة بموقع اللافتة. المسافة هي كمية قياسية. معرفة المسافة وحدها لا تكفي للوصول إلى المدينة؛ يجب أن نعرف أيضًا الاتجاه من اللافتة إلى المدينة. الاتجاه، مع المسافة، عبارة عن كمية متجهة تسمى عادة متجه الإزاحة. لذلك، تقدم اللافتة معلومات حول متجهات الإزاحة أو المتجهات من اللافتة إلى المدن.

• مخطط الفصل

1. الكميات القياسية والكميات المتجهة
2. تحليل المتجهات والنظام الإحداثي الديكارتي
3. الإحداثيات القطبية في بعدين وفي ثلاثة أبعاد
4. جبر المتجهات وحل معادلات المتجهات
5. ضرب المتجهات

ما هي المتجهات

المتجهات Vectors ضرورية في الرياضيات والفيزياء والهندسة. العديد من الكميات الفيزيائية الأساسية هي متجهات، بما في ذلك الإزاحة والسرعة والقوة والمجالات الكهربائية والمغناطيسية المتجهة. يحدد حاصل الضرب القياسي للمتجهات الكميات الفيزيائية العددية الأساسية الأخرى، مثل الطاقة. حاصل الضرب الاتجاهي للمتجهات يحدد كميات فيزيائية أساسية أخرى، مثل عزم الدوران والزخم الزاوي. بعبارة أخرى، المتجهات هي جزء مكون من الفيزياء إلى حد كبير بنفس الطريقة التي تعتبر بها الجمل جزءًا مكونًا من الأدب.

في الفيزياء التمهيدية، المتجهات هي كميات إقليدية لها تمثيلات هندسية كسهام في بعد واحد (في خط)، في بعدين (في مستوى)، أو في ثلاثة أبعاد (في الفضاء). يمكن جمعها أو طرحها أو ضربها. في هذا الفصل، نستكشف عناصر الجبر المتجه لتطبيقات في الميكانيكا والكهرباء والمغناطيسية. عمليات المتجهات لها أيضًا تعميمات عديدة في فروع الفيزياء الأخرى.

الكميات القياسية والكميات المتجهة

الأهداف:

بنهاية هذا القسم، ستكون قادرًا على:

• وصف الفرق بين الكميات المتجهة والكميات القياسية.
• تحديد مقدار واتجاه المتجه.
• شرح تأثير ضرب كمية متجهة بعدد قياسي.
• وصف كيفية جمع الكميات المتجهة أحادية البعد أو طرحها.
• شرح التركيب الهندسي لجمع أو طرح المتجهات في المستوى.
• التمييز بين المعادلة المتجهة والمعادلة العددية.

يمكن تحديد العديد من الكميات المادية المألوفة تمامًا عن طريق إعطاء عدد واحد والوحدة المناسبة. على سبيل المثال، “مدة الفصل الدراسي 50 دقيقة” أو “سعة خزان الوقود في سيارتي 65 لترًا” أو “المسافة بين لافتتين هي 100 متر”. الكمية الفيزيائية التي يمكن تحديدها بالكامل بهذه الطريقة تسمى الكمية القياسية Scalar Quantity. وكلمة Scalar مرادف لكلمة “قياس”. الوقت والكتلة والمسافة والطول والحجم ودرجة الحرارة والطاقة أمثلة على الكميات القياسية.

يمكن إضافة أو طرح الكميات القياسية أو العددية التي لها نفس الوحدات الفيزيائية وفقًا لقواعد الجبر المعتادة للأعداد. على سبيل المثال، الفصل الذي ينتهي قبل 10 دقائق من 50 دقيقة يستمر 50 دقيقة – 10 دقائق = 40 دقيقة. وبالمثل، فإن حصة 60 كالوري من الذرة متبوعة بـ 200 كالوري من الكعك تعطي 60 كالوري + 200 كالوري = 260 كالوري من الطاقة. عندما نضرب كمية قياسية في عدد، نحصل على نفس الكمية القياسية ولكن بقيمة أكبر (أو أصغر). على سبيل المثال، إذا كان إفطار الأمس يحتوي على 200 سعرة حرارية من الطاقة ووجبة الإفطار اليوم تحتوي على أربعة أضعاف الطاقة التي كانت بالأمس، فإن فطور اليوم يحتوي على 4 × (200 سعرة حرارية) = 800 سعرة حرارية من الطاقة.

يمكن أيضًا ضرب أو قسمة كميتين قياسيتين على بعضهما البعض لتكوين كمية قياسية مشتقة. على سبيل المثال، إذا قطع قطار مسافة 100 كم في 1.0 ساعة، تكون سرعته 100.0 كم/ 1.0 ساعة = 27.8 م/ث، حيث السرعة هي كمية قياسية مشتقة يتم الحصول عليها بقسمة المسافة على الزمن.

الفرق بين الكميات المتجهة والكميات القياسية

ومع ذلك، لا يمكن وصف العديد من الكميات الفيزيائية تمامًا من خلال عدد واحد فقط من الوحدات المادية. على سبيل المثال، عندما يرسل خفر السواحل الأمريكي سفينة أو طائرة هليكوبتر لمهمة إنقاذ، يجب أن يعرف فريق الإنقاذ ليس فقط المسافة إلى إشارة الاستغاثة، ولكن أيضًا الاتجاه الذي تأتي منه الإشارة حتى يتمكنوا من الوصول إلى مصدرها بأسرع ما يمكن. الكميات المادية المحددة تمامًا بإعطاء عدد من الوحدات (المقدار) والاتجاه تسمى الكميات المتجهة Vector Quantities. تتضمن أمثلة الكميات المتجهة الإزاحة والسرعة والموضع والقوة وعزم الدوران. في لغة الرياضيات، يتم تمثيل الكميات المتجه الفيزيائية بواسطة كائنات رياضية تسمى المتجهات (الشكل 2.2). يمكننا جمع أو طرح متجهين، ويمكننا ضرب متجه في عدد قياسي أو متجه آخر، لكن لا يمكننا القسمة على متجه. لم يتم تعريف عملية القسمة على المتجه.

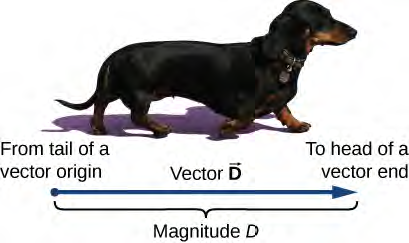
الشكل 2.2 نرسم متجهًا من النقطة الأولية أو الأصل (يسمى “ذيل” المتجه) إلى النهاية أو النقطة النهائية (تسمى “رأس” المتجه)، مميزة برأس السهم. المقدار هو طول المتجه ودائمًا ما يكون كمية قياسية موجبة.

الرسم البياني للمتجهات

دعونا نفحص جبر المتجهات Vector Algebra باستخدام طريقة رسومية للتعرف على المصطلحات الأساسية وتطوير الفهم النوعي. ومع ذلك، من الناحية العملية، عندما يتعلق الأمر بحل مسائل الفيزياء، فإننا نستخدم طرقًا تحليلية، والتي سنراها في القسم التالي. تعتبر الطرق التحليلية أكثر بساطة من الناحية الحسابية وأكثر دقة من الطرق الرسومية.

من الآن فصاعدًا، للتمييز بين المتجه والكمية القياسية، نعتمد الاصطلاح الشائع القائل بأن الحرف المكتوب بخط عريض مع سهم فوقه يشير إلى متجه، والحرف الذي لا يحتوي على سهم يشير إلى الكمية القياسية. على سبيل المثال، المسافة التي تبلغ 2.0 كم، وهي كمية قياسية، يُرمز إليها بـ d = 2.0 km، في حين يُرمز إلى الإزاحة التي مقدارها 2.0 كلم في اتجاه ما، وهي كمية متجهة، بواسطة الرمز:

لنفترض أنك أخبرت صديقًا في رحلة تخييم أنك اكتشفت حفرة صيد رائعة على بعد 6 كم من خيمتك. من غير المحتمل أن يتمكن صديقك من العثور على الحفرة بسهولة إلا إذا قمت أيضًا بإبلاغ الاتجاه الذي يمكن العثور عليه فيه فيما يتعلق بموقع المخيم الخاص بك. يمكنك أن تقول، على سبيل المثال، “امشي على بعد حوالي 6 كيلومترات شمال شرق خيمتي”. المفهوم الأساسي هنا هو أنه لا يجب عليك إعطاء معلومة واحدة بل معلومتين – أي المسافة أو المقدار (6 كم) والاتجاه (شمال شرق).

الإزاحة مصطلح عام يستخدم لوصف التغيير في الموضع، مثل الإزاحة أثناء الرحلة من الخيمة إلى حفرة الصيد.

الإزاحة مثال على كمية متجه

إذا كنت تمشي من الخيمة (الموقع A) إلى الحفرة (الموقع B)، كما هو موضح في الشكل 2.3 ، فإن المتجه D →، الذي يمثل إزاحتك، يتم رسمه كسهم ينشأ عند النقطة A وينتهي عند النقطة B. يمثل رأس السهم نهاية المتجه. اتجاه متجه الإزاحة D → هو اتجاه السهم. يمثل طول السهم مقدار D للمتجه D →. وهنا D = 6 km. نظرًا لأن حجم المتجه هو طوله، وهو عدد موجب، فإن المقدار يُشار إليه أيضًا بوضع تدوين القيمة المطلقة حول الرمز الذي يشير إلى المتجه؛ لذلك، يمكننا أن نكتب بشكل مكافئ أن D | ≡ D → |. لحل مسألة المتجه بيانياً، نحتاج إلى رسم المتجه D → لقياسه.

على سبيل المثال، إذا افترضنا أن وحدة واحدة للمسافة (1 كم) ممثلة في الرسم بقطعة مستقيمة بطول u = 2 سم، فسيتم تمثيل الإزاحة الكلية في هذا المثال بمتجه طوله d = 6 ش = 6 ( 2 سم) = 12 سم، كما هو موضح في الشكل 2.4. لاحظ أنه لتجنب الالتباس، استخدمنا D = 6 km للإشارة إلى حجم الإزاحة الفعلية و d = 12 cm للإشارة إلى طول تمثيلها في الرسم.

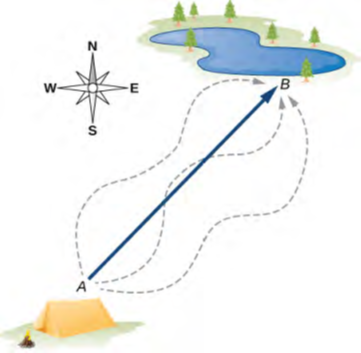
الشكل 2.3: يُشار إلى متجه الإزاحة من النقطة A (الموضع الأولي في موقع المخيم) إلى النقطة B (الموضع النهائي عند فتحة الصيد) بسهم مع الأصل عند النقطة A والنهاية عند النقطة B. وتكون الإزاحة هي نفسها بالنسبة إلى أي من المسارات الفعلية (المنحنيات المتقطعة) التي يمكن اتخاذها بين النقطتين A و B.

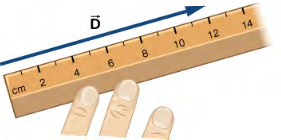
الشكل 2.4: يتم رسم الإزاحة D→ التي تبلغ قيمتها 6 كيلومترات للمقياس كمتجه بطول 12 سم عندما يمثل طول 2 سم وحدة إزاحة واحدة (في هذه الحالة تساوي كيلومترًا واحدًا).

مثال توضيحي

لنفترض أن صديقك يسير من موقع المخيم في A إلى بركة الصيد في B ثم يمشي للخلف: من بركة الصيد في B إلى موقع المخيم في A. حجم متجه الإزاحة D→ AB من A إلى B هو نفسه حجم متجه الإزاحة D→ BA من B إلى A (يساوي 6 كم في كلتا الحالتين)، لذلك يمكننا كتابة DAB = DBA. ومع ذلك، فإن المتجه D→ AB لا يساوي المتجه D→ BA لأن هذين المتجهين لهما اتجاهات مختلفة: D→ AB ≠ D→ BA. في الشكل 2.3، المتجه D → BA سيتم تمثيله بواسطة متجه ذو أصل عند النقطة B ونهاية عند النقطة A، مما يشير إلى المتجه D→ BA يشير إلى الجنوب الغربي، وهو بالضبط 180 درجة عكس اتجاه المتجه D→ AB.

نقول أن المتجه D→ BA معاكس موازٍ للمتجه D→ AB ويكتب D→ AB = – D→ BA، حيث تشير علامة السالب إلى الاتجاه الموازي.

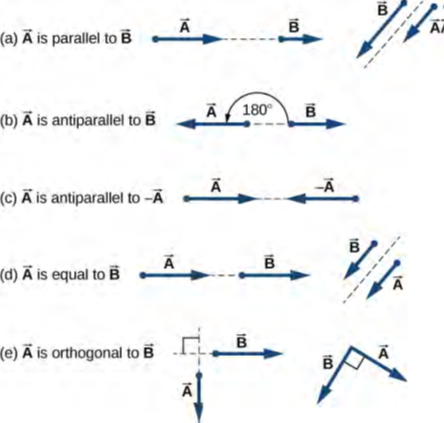
يُقال إن متجهين لهما اتجاهات متطابقة متجهات متوازية – بمعنى أنهما متوازيان مع بعضهما البعض. متجهان متوازيان A→ و B→ متساويان، يُشار إليهما بالرمز ، إذا وفقط إذا كان لهما مقادير متساوية يُقال إن متجهين لهما اتجاهات متعامدة مع بعضهما البعض هما متجهان متعامدان. هذه العلاقات بين المتجهات موضحة في الشكل 2.5.

تحقق من فهمك

يتحرك زورقان بخاريان يُدعى أليس وبوب على بحيرة. بالنظر إلى المعلومات حول متجهات السرعة الخاصة بهم في كل من المواقف التالية، وضح ما إذا كانت متجهات السرعة الخاصة بهم متساوية أو غير ذلك. (أ) تتحرك أليس شمالًا بسرعة 6 عقدة ويتحرك بوب غربًا بسرعة 6 عقدة. (ب) تتحرك أليس غربًا بسرعة 6 عقدة ويتحرك بوب غربًا بسرعة 3 عقدة. (ج) تتحرك أليس باتجاه الشمال الشرقي بسرعة 6 عقدة ويتحرك بوب جنوبًا بسرعة 3 عقدة. (د) تتحرك أليس باتجاه الشمال الشرقي بسرعة 6 عقدة ويتحرك بوب باتجاه الجنوب الغربي بسرعة 6 عقدة. (هـ) تتحرك أليس باتجاه الشمال الشرقي بسرعة 2 عقدة ويتحرك بوب بالقرب من الشاطئ الشمالي الشرقي بسرعة 2 عقدة.

جبر المتجهات في بعد واحد

يمكن ضرب المتجهات بواسطة القيم العددية، أو جمعها إلى متجهات أخرى، أو طرحها من متجهات أخرى. يمكننا توضيح مفاهيم المتجهات هذه باستخدام مثال لرحلة الصيد الموضحة في الشكل 2.6.

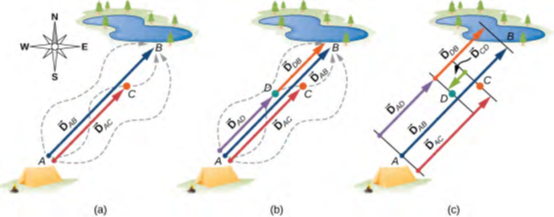
الشكل 2.6 متجهات الإزاحة لرحلة صيد. (a) التوقف للراحة عند النقطة C أثناء السير من المعسكر (النقطة A) إلى البحيرة (النقطة B). (b) العودة لصندوق المعالجة الذي وقع عند (النقطة D). (c) الانتهاء في بحيرة الصيد.

افترض أن صديقك غادر من النقطة أ (موقع المخيم) وسار في الاتجاه إلى النقطة ب (بحيرة الصيد)، لكنه توقف على طول الطريق للراحة عند نقطة ما (ج) تقع على بعد ثلاثة أرباع المسافة بين A وB، بداية من النقطة أ (الشكل 2.6 (a)). ما متجه إزاحته D → AC عندما يصل إلى النقطة C؟ نعلم أنه إذا سار على طول الطريق إلى B، فإن متجه الإزاحة بالنسبة إلى A هو D → AB، والذي تبلغ قيمته المطلقة DAB = 6 كم واتجاه الشمال الشرقي. إذا سار على مسافة 0.75 فقط من المسافة الإجمالية، محافظًا على الاتجاه الشمالي الشرقي، عند النقطة C، يجب أن يكون 0.75DAB = 4.5 كيلومترًا من موقع المخيم في A km = 0.75DAB وهي موازية لمتجه الإزاحة D → AB. يمكن ذكر كل هذا بإيجاز في شكل معادلة المتجه التالية:

D → AC = 0.75 D → AB

في معادلة المتجه، كلا طرفي المعادلة متجهان. المعادلة السابقة هي مثال لمتجه مضروب في عدد قياسي موجب (رقم) α = 0.75. نتيجة هذا الضرب هو المتجه D → AC، وهو متجه جديد مع اتجاه موازٍ لاتجاه المتجه الأصلي D → AB.

ضرب المتجه بعدد قياسي

بشكل عام، عندما يتم ضرب المتجه A → في عدد موجب α، تكون النتيجة متجهًا جديدًا B → الذي يوازي A → ـ أي أن:

(2.1)

القيمة المطلقة Magnitude للمتجه | B → | الجديد يتم حسابها بضرب القيمة المطلقة للمتجه الأصلي | A → | بقيمة العدد الموجب، كما تعبر عنه المعادلة القياسية التالية:

B = | α | A

(2.2)

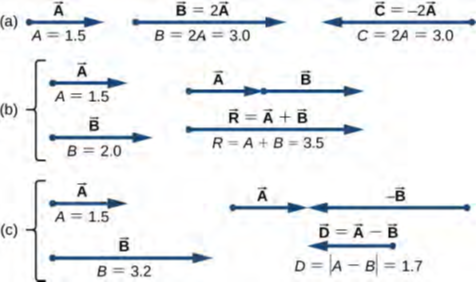
في المعادلة القياسية، كلا طرفي المعادلة عبارة عن أعداد. المعادلة 2.2 هي معادلة قياسية (عددية) لأن القيم المطلقة للمتجهات هي كميات عددية (وأرقام موجبة). إذا كان العدد القياسي α سالبًا في معادلة المتجه 2.1، فإن القيمة العددية | ب → | من المتجه الجديد لا تزال تعطى بواسطة المعادلة 2.2، لكن اتجاه المتجه الجديد B → يكون عكسيًا لاتجاه A →. يتم توضيح هذه المبادئ في الشكل 2.7 (أ) من خلال مثالين حيث يكون طول المتجه A → 1.5 وحدة. عندما تكون α = 2 ، فإن المتجه الجديد B → = 2 A → له طول B = 2A = 3.0 وحدة (ضعف طول المتجه الأصلي) ويكون موازيًا للمتجه الأصلي. عندما تكون α = −2، فإن المتجه الجديد:

له طول يساوي C = | – 2 | A = 3.0 وحدة (ضعف طول المتجه الأصلي) وهو في اتجاه عكسي موازي لاتجاه المتجه الأصلي.

وصف الشكل

افترض الآن أن صديقك في الصيد قد غادر من النقطة A (موقع المخيم)، وسار في الاتجاه إلى النقطة B (حفرة الصيد)، لكنه أدرك أنه فقد صندوق أدوات الصيد الخاص به عندما توقف للراحة عند النقطة C (تقع على بعد ثلاثة أرباع المسافة إلى منطقة الصيد). المسافة بين A و B، ابتداء من النقطة A. لذلك، عاد إلى الوراء وأعاد تتبع خطواته في الاتجاه نحو موقع المخيم ووجد الصندوق ملقى على الطريق في نقطة ما D على بعد 1.2 كم فقط من النقطة C (انظر الشكل 2.6 (b)). ما متجه إزاحته D → AD عندما يجد الصندوق عند النقطة D؟ ما متجه إزاحته D→ DB من النقطة D إلى الحفرة؟

توضيح الفكرة

لقد أثبتنا بالفعل أن متجه الإزاحة عند نقطة السكون C هو D→ _AC = 0.75 D→ _AB. بدءًا من النقطة C، يسير جنوب غربًا (باتجاه موقع المخيم)، مما يعني أن متجه الإزاحة الجديد D→ _CD من النقطة C إلى النقطة D هو المتجه العكسي والموازي لـ D→ _AB. قيمته المطلقة | D→ _CD | هو DCD = 1.2 كم = 0.2DAB، لذا فإن متجه الإزاحة الثاني هو D→ _CD = −0.2 D→ _AB. إن إزاحته الإجمالية D → _AD بالنسبة إلى موقع المخيم هي مجموع متجه لمتجهي الإزاحة: المتجه D→_AC (من موقع المخيم إلى نقطة الاستراحة) والمتجه D→ _CD (من نقطة الاستراحة إلى النقطة التي وجدها فيها صندوق):

(2.3)

يُطلق على مجموع المتجهين (أو أكثر) المتجه الناتج أو، باختصار، الناتج. عندما تكون المتجهات الموجودة على الجانب الأيمن من المعادلة 2.3 معروفة، يمكننا إيجاد الناتج D→ _AD على النحو التالي:

(2.4)

عندما يصل صديقك أخيرًا إلى البركة عند B، فإن متجه الإزاحة D→ _AB من النقطة A هو مجموع متجه لمتجه الإزاحة D→ _AD من النقطة A إلى النقطة D ومتجه الإزاحة D→ _DB من النقطة D إلى فتحة الصيد:

(2.5)

ملاحظة

لاحظ أن الاختلاف بين متجهين ليس أكثر من مجموع متجه لمتجهين لأن المصطلح الثاني في المعادلة 2.5 متجه – D→_AD (وهو عكس D→ _AD). عندما نستبدل المعادلة 2.4 في المعادلة 2.5  نحصل على متجه الإزاحة الثاني:

(2.6)

تعني هذه النتيجة أن صديقك مشى D_DB = 0.45D_AB = 0.45 (6.0 كيلومترات) = 2.7 كم من النقطة التي وجد فيها صندوق المعالجة الخاص به إلى فتحة الصيد.

عندما تقع المتجهات A → و B → على طول خط (أي في بعد واحد)، كما هو الحال في مثال التخييم، فإن الناتج R → = A → + B → والفرق بينهما D → = A → – B → كلاهما يقع على طول نفس الاتجاه. يمكننا توضيح إضافة أو طرح المتجهات عن طريق رسم المتجهات المقابلة للقياس في بعد واحد، كما هو موضح في الشكل 2.7.

لتوضيح النتيجة عندما يكون A → و B → متجهين متوازيين، نرسمهما على طول خط واحد عن طريق وضع أصل متجه واحد في نهاية المتجه الآخر بطريقة الرأس إلى الذيل (انظر الشكل 2.7 (b)). القيمة العددية لهذا الناتج هو مجموع مقاديرها: R = A + B. اتجاه الناتج موازٍ لكلا المتجهين. عندما يكون المتجه A → مضادًا للتوازي مع المتجه B →، فإننا نرسمه على طول خط واحد إما بطريقة رأسية (الشكل 2.7 (c)) أو بطريقة الذيل الكامل. القيمة العددية للفرق المتجه، إذن، هو القيمة المطلقة D = | A – B | للفرق بين مقاديرها. اتجاه متجه الفرق D → موازٍ لاتجاه المتجه الأطول.

خاصية التبادلية والترابطية

بشكل عام، في بُعد واحد – وكذلك في الأبعاد الأعلى، مثل المستوى أو في الفضاء – يمكننا إضافة أي عدد من المتجهات ويمكننا القيام بذلك بأي ترتيب لأن إضافة المتجهات تكون تبادلية:

(2.7)

وترابطية:

(2.8)

علاوة على ذلك، فإن الضرب بواسطة قيمة عددية يكون توزيعيًا:

(2.9)

استخدمنا خاصية التوزيع في المعادلة 2.4 والمعادلة 2.6.

عند إضافة العديد من المتجهات في بُعد واحد، يكون من الملائم استخدام مفهوم متجه الوحدة. متجه الوحدة، الذي يُشار إليه برمز حرف بقبعة، مثل u^، له حجم واحد ولا يحتوي على أي وحدة مادية بحيث u^| ≡ u = 1|. الدور الوحيد لمتجه الوحدة هو تحديد الاتجاه. على سبيل المثال، بدلاً من أن نقول أن المتجه D → AB يبلغ حجمه 6.0 كم واتجاه الشمال الشرقي، يمكننا تقديم متجه الوحدة u^ الذي يشير إلى الشمال الشرقي ونقول بإيجاز أن:

ثم يتم تحديد الاتجاه الجنوبي الغربي ببساطة بواسطة متجه الوحدة −u^. بهذه الطريقة، يتم التعبير عن إزاحة 6.0 كم في الاتجاه الجنوبي الغربي بواسطة المتجه:

مثال تطبيقي: الخنفساء ووكر

عصا قياس طويلة موضوعة على جدار في معمل فيزيائي بطرفها 200 سم على الأرض. تهبط خنفساء على علامة 100 سم وتزحف بشكل عشوائي على طول العصا. يمشي أولاً 15 سم نحو الأرض ، ثم يمشي 56 سم باتجاه الحائط ، ثم يمشي 3 سم نحو الأرض مرة أخرى. ثم ، بعد توقف قصير ، يستمر لمسافة 25 سم نحو الأرض ثم ، مرة أخرى ، يزحف لأعلى بمقدار 19 سم باتجاه الحائط قبل أن يصل إلى فترة راحة كاملة (الشكل 2.8). أوجد متجه الإزاحة الكلية وموضع الراحة الأخير على العصا.

إستراتيجية الحل

إذا اخترنا الاتجاه على طول العصا نحو الأرض باعتباره اتجاه متجه الوحدة u ^، فإن الاتجاه نحو الأرض هو + u ^ والاتجاه نحو الحائط هو −u ^. تقوم الخنفساء بإجمالي خمس عمليات إزاحة:

الإزاحة الكلية D → هي نتيجة جميع متجهات الإزاحة.

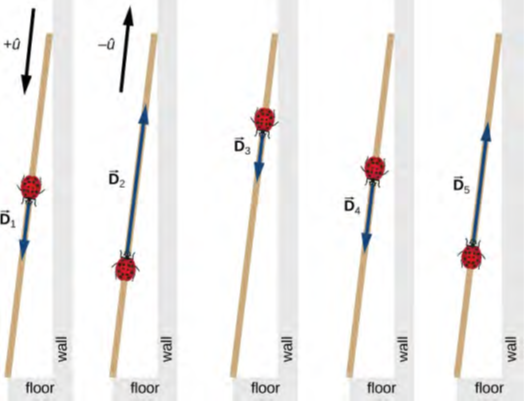
الشكل 2.8 خمس متجهات إزاحة للخنفساء. لاحظ أنه في هذا الرسم التخطيطي، لا يتم رسم مقاييس الإزاحة على نطاق واسع.

الحل

ناتج جميع متجهات الإزاحة هو:

في هذا الحساب، نستخدم قانون التوزيع المعطى في المعادلة 2.9. تقرأ النتيجة أن متجه الإزاحة الكلي يشير بعيدًا عن علامة 100 سم (موقع الهبوط الأولي) باتجاه نهاية عصا العداد التي تلامس الجدار. يتم تحديد النهاية التي تلامس الجدار بـ 0 سم، لذلك يكون الموضع النهائي للخنفساء عند علامة (100-32) سم = 68 سم.

تحقق من فهمك

غواص الكهوف يدخل نفق طويل تحت الماء. عندما تكون إزاحته فيما يتعلق بنقطة الدخول 20 مترًا، فإنه يسقط الكاميرا عن طريق الخطأ، لكنه لا يلاحظ أنها مفقودة حتى يكون على بعد حوالي 6 أمتار داخل النفق. يسبح إلى الوراء 10 أمتار لكنه لا يجد الكاميرا، لذلك قرر إنهاء الغوص. كم يبعد هذا الغواص عن نقطة الدخول؟ بأخذ الاتجاه الموجب للخروج من النفق، ما هو متجه الإزاحة للغواض بالنسبة إلى نقطة الدخول؟

جبر المتجهات في بعدين

عندما تقع المتجهات في مستوى – أي عندما تكون في بعدين – يمكن ضربها بالكميات، أو إضافتها إلى متجهات أخرى، أو طرحها من المتجهات الأخرى وفقًا للقوانين العامة المعبر عنها بالمعادلة 2.1، المعادلة 2.2، المعادلة 2.7، والمعادلة 2.8. ومع ذلك، فإن قاعدة الجمع لمتجهين في المستوى تصبح أكثر تعقيدًا من قاعدة الجمع المتجهات في بعد واحد. علينا استخدام قوانين الهندسة لإنشاء المتجهات الناتجة، متبوعة بعلم المثلثات للعثور على مقادير المتجهات والاتجاهات. يشيع استخدام هذا النهج الهندسي في الملاحة (الشكل 2.9). في هذا القسم، نحتاج إلى وجود مسطرتين، ومثلث، ومنقلة، وقلم رصاص، وممحاة لرسم المتجهات للقياس بالتركيبات الهندسية.

الشكل 2.9 في الملاحة، تُستخدم قوانين الهندسة لرسم عمليات الإزاحة الناتجة على الخرائط الملاحية.

للبناء هندسي لمجموع متجهين في المستوى، نتبع قاعدة متوازي الأضلاع. افترض أن متجهين A → و B → في المواضع الأصلية الموضحة في الشكل 2.10. قم بترجمة أحدهما بالتوازي مع بداية المتجه الآخر، بحيث يكون لكلا المتجهين أصولهما في نفس النقطة بعد الترجمة. الآن، في نهاية المتجه A → نرسم خطًا موازيًا للمتجه B → وفي نهاية المتجه B→ نرسم خطًا موازٍ للمتجه A → (الخطوط المتقطعة في الشكل 2.10). بهذه الطريقة نحصل على متوازي الأضلاع. من أصل المتجهين، نرسم قطريًا يكون الناتج R → للمتجهين: R =→ A + →B → (الشكل 2.10 (أ)). القطر الآخر لهذا المتوازي الأضلاع هو الفرق المتجه للمتجهين D = → A – → B →، كما هو موضح في الشكل 2.10 (ب). لاحظ أن نهاية متجه الفرق موضوعة في نهاية المتجه A →.

قاعدة متوازي الأضلاع

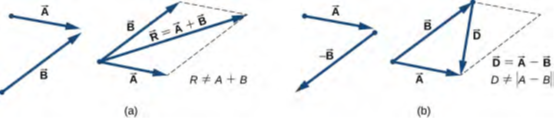
شكل 2.10 قاعدة متوازي الأضلاع لجمع متجهين. قم بإجراء الترجمة المتوازية لكل متجه إلى نقطة حيث تتطابق أصولها (المميزة بالنقطة) وقم ببناء متوازي أضلاع مع جانبين على المتجهات والجانبين الآخرين (المشار إليهما بخطوط متقطعة) بالتوازي مع المتجهات. (أ) ارسم المتجه الناتج R → على طول قطري متوازي الأضلاع من النقطة المشتركة إلى الزاوية المقابلة. الطول R للمتجه الناتج لا يساوي مجموع مقادير المتجهين. (ب) ارسم متجه الفرق D → = A → – → B على طول القطر الذي يربط نهايات المتجهات. ضع أصل المتجه D → في نهاية المتجه B → ونهاية (رأس السهم) للمتجه D → في نهاية المتجه A →. الطول D لمتجه الفرق لا يساوي فرق مقادير المتجهين.

ويترتب على قاعدة متوازي الأضلاع أنه لا يمكن التعبير عن مقدار المتجه الناتج ولا مقدار متجه الفرق كمجموع أو فرق بسيط في المقدارين A و B، لأنه لا يمكن التعبير عن طول القطر كمجموع بسيط لـ أطوال الضلعين. عند استخدام بنية هندسية لإيجاد المقادير | R → | و | D → |، علينا استخدام قوانين حساب المثلثات، مما قد يؤدي إلى جبر معقد. هناك طريقتان للتحايل على هذا التعقيد الجبري. إحدى الطرق هي استخدام طريقة المكونات، والتي ندرسها في القسم التالي. الطريقة الأخرى هي رسم المتجهات لتوسيع نطاقها، كما هو الحال في الإزاحة، وقراءة أطوال المتجهات والزوايا التقريبية (الاتجاهات) من الرسوم البيانية. في هذا القسم ندرس النهج الثاني.

جمع ثلاث متجهات أو أكثر

إذا احتجنا إلى جمع ثلاث متجهات أو أكثر، فإننا نكرر قاعدة متوازي الأضلاع لأزواج المتجهات حتى نجد محصلة جميع المحصلات. بالنسبة لثلاثة متجهات إزاحة، على سبيل المثال، نجد أولاً ناتج المتجه 1 والمتجه 2، ثم نجد نتيجة هذا الناتج مع المتجه 3. الترتيب الذي نختار به أزواج المتجهات لا يهم لأن عملية جمع المتجهات هي تبادلية وترابطية (انظر المعادلة 2.7 والمعادلة 2.8). قبل أن نذكر قاعدة عامة تُتبع مع التطبيقات المتكررة لقاعدة متوازي الأضلاع، دعنا نلقي نظرة على المثال التالي.

لنفترض أنك تخطط لرحلة إجازة في فلوريدا. عند المغادرة من تالاهاسي، عاصمة الولاية، تخطط لزيارة عمك جو في جاكسونفيل، ورؤية ابن عمك فيني في دايتونا بيتش، والتوقف للحصول على القليل من المرح في أورلاندو، ومشاهدة عرض السيرك في تامبا، وزيارة جامعة فلوريدا في غينزفيل. قد يتم تمثيل مسارك بخمسة متجهات إزاحة A → و B → و C → و D → و E →، والتي يُشار إليها بالمتجهات الحمراء في الشكل 2.11. ما هو إجمالي إزاحتك عندما تصل إلى غينزفيل Gainesville؟ الإزاحة الكلية هي مجموع المتجهات لجميع متجهات الإزاحة الخمسة، والتي يمكن إيجادها باستخدام قاعدة متوازي الأضلاع أربع مرات. بدلاً من ذلك، تذكر أن متجه الإزاحة له بدايته في الموضع الأولي (تالاهاسي) ونهايته في الموضع النهائي (غينزفيل)، لذلك يمكن رسم متجه الإزاحة الكلي مباشرةً كسهم يربط تالاهاسي بـ غينزفيل Gainesville (انظر المتجه الأخضر في الشكل 2.11).

عندما نستخدم قاعدة متوازي الأضلاع أربع مرات، فإن الناتج R → الذي نحصل عليه هو بالضبط هذا المتجه الأخضر الذي يربط تالاهاسي بـ غينزفيل:

استخدام قاعدة متوازي الأضلاع عدة مرات

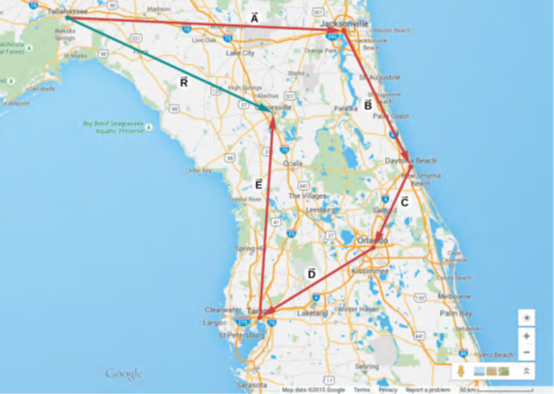
الشكل 2.11 عندما نستخدم قاعدة متوازي الأضلاع أربع مرات، نحصل على المتجه الناتج: R⃗ =A⃗ +B⃗ +C⃗ +D⃗ +E⃗، وهو المتجه الأخضر الذي يربط Tallahassee بـ Gainesville.

يمكن تعميم المتجه الناتج للعديد من المتجهات باستخدام البناء الهندسي التالي من الذيل إلى الرأس. لنفترض أننا نريد رسم المتجه الناتج R → لأربعة متجهات A → و B → و C → و D → (الشكل 2.12 (أ)). نختار أيًا من المتجهات باعتباره المتجه الأول ونقوم بترجمة موازية لمتجه ثانٍ إلى موضع حيث يتطابق أصل (“الذيل”) للمتجه الثاني مع نهاية (“رأس”) المتجه الأول. بعد ذلك، نختار متجهًا ثالثًا ونقوم بترجمة متوازية للمتجه الثالث إلى موضع يتزامن فيه أصل المتجه الثالث مع نهاية المتجه الثاني. نكرر هذا الإجراء حتى تصبح جميع المتجهات في ترتيب من الرأس إلى الذيل مثل ذلك الموضح في الشكل 2.12.

نرسم المتجه الناتج R → عن طريق ربط أصل (“الذيل”) للمتجه الأول بنهاية (“الرأس”) للمتجه الأخير. نهاية المتجه الناتج تكون عند نفس نهاية المتجه الأخير. نظرًا لأن إضافة المتجهات هي عملية ترابطية وتبادلية، فإننا نحصل على نفس المتجه الناتج بغض النظر عن المتجه الذي نختاره ليكون أولًا أو ثانيًا أو ثالثًا أو رابعًا في هذا البناء.

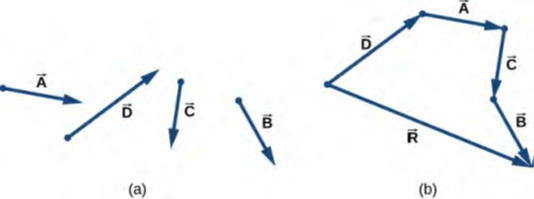
الشكل 2.12 طريقة الذيل إلى الرأس لرسم المتجه الناتج R⃗ =A⃗ +B⃗ +C⃗ +D⃗. (أ) أربع متجهات ذات أحجام واتجاهات مختلفة. (ب) يتم ترجمة المتجهات الموجودة في (أ) إلى مواضع جديدة حيث يكون أصل (“الذيل”) لأحد المتجهات في نهاية (“الرأس”) للمتجه الآخر. يتم رسم المتجه الناتج من أصل (“الذيل”) للمتجه الأول إلى نهاية (“الرأس”) للمتجه الأخير في هذا الترتيب.

مثال تطبيقي: البناء الهندسي للنتيجة

تم تحديد متجهات الإزاحة الثلاثة A، → B → ، و C → في الشكل 2.13 بمقاديرها A = 10.0، B = 7.0 ، و C = 8.0، على التوالي، وزوايا الاتجاه الخاصة بكل منها مع الاتجاه الأفقي α = 35 ° ، β = -110 درجة، و γ = 30 درجة. الوحدات الفيزيائية للمقادير هي السنتيمتر. اختر مقياسًا مناسبًا واستخدم مسطرة ومنقلة لإيجاد مجاميع المتجهات التالية: (أ) R⃗ =A⃗ +B⃗، (ب) D⃗ =A⃗ −B⃗ , and، و (ج) S⃗ =A⃗ −3B⃗ +C⃗.

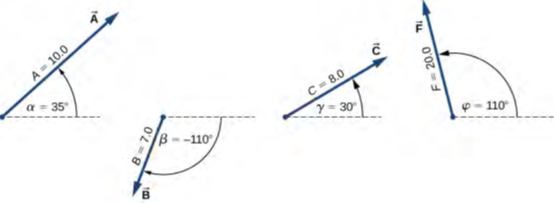
الشكل 2.13: البناء الهندسي لنتيجة جميع المتجهات المستخدمة في المثال 2.2 وفي ميزة التحقق من الفهم التالية.

إستراتيجية الحل

في البناء الهندسي، لإيجاد متجه يعني إيجاد مقدارها وزاوية اتجاهها مع الاتجاه الأفقي. تتمثل الإستراتيجية في رسم المتجهات التي تظهر على الجانب الأيمن من المعادلة وبناء المتجه الناتج. ثم استخدم مسطرة ومنقلة لقراءة مقدار الناتج وزاوية الاتجاه. بالنسبة للجزئين (أ) و (ب)، نستخدم قاعدة متوازي الأضلاع. ل (ج) نستخدم طريقة الذيل لرأس.

الحل

بالنسبة للجزئين (أ) و (ب)، نربط أصل المتجه B → بأصل المتجه A →، كما هو موضح في الشكل 2.14، وننشئ متوازي أضلاع. القطر الأقصر لهذا المتوازي الأضلاع هو مجموع A → + B →. أطول الأقطار هو الفرق A → – B →، نستخدم مسطرة لقياس أطوال الأقطار، ومنقلة لقياس الزوايا مع الأفقي. بالنسبة للنتيجة R →، نحصل على R = 5.8 سم و θR ≈ 0 درجة. بالنسبة للفرق D →، نحصل على D = 16.2 سم و D = 49.3 درجة، والتي تظهر في الشكل 2.14.

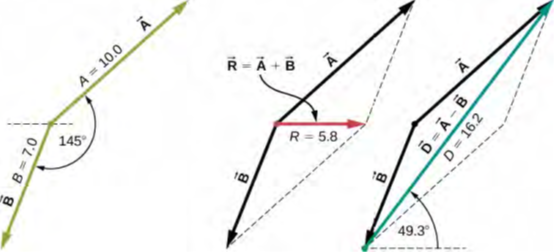
الشكل 2.14 استخدام قاعدة متوازي الأضلاع لحل (أ) (إيجاد الناتج، أحمر) و (ب) (إيجاد الفرق، أزرق).

بالنسبة إلى (ج)، يمكننا البدء بالمتجه −3B → ورسم المتجهات المتبقية ذيلًا للرأس كما هو موضح في الشكل 2.15.

بالإضافة إلى المتجهات، الترتيب الذي نرسم به المتجهات غير مهم، لكن رسم المتجهات للقياس مهم جدًا. بعد ذلك ، نرسم المتجه S → من أصل المتجه الأول إلى نهاية المتجه الأخير ونضع رأس السهم في نهاية S →. نستخدم مسطرة لقياس طول S →، ونجد أن مقدارها S = 36.9 cm، ونستخدم المنقلة ونجد أن زاوية اتجاهها هي θ_S = 52.9 °. يظهر هذا الحل في الشكل 2.15.

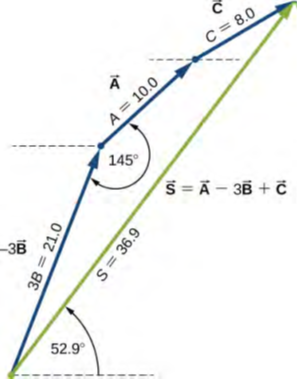
الشكل 2.15 استخدام طريقة الذيل لرأس لحل (ج) (إيجاد المتجه S → ، الأخضر).

تحقق من فهمك

باستخدام متجهات الإزاحة الثلاثة A → و B → و F → في الشكل 2.13، اختر مقياسًا مناسبًا واستخدم مسطرة ومنقلة للعثور على المتجه G → المعطى بواسطة معادلة المتجه:

المصدر

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.