الكتلة والوزن والفرق بينهما

مفهوم الكتلة والوزن

غالبًا ما يتم استخدام الكتلة والوزن بالتبادل في المحادثة اليومية. على سبيل المثال، غالبًا ما تُظهر سجلاتنا الطبية وزننا بالكيلوجرام ولكن ليس بالوحدات الصحيحة للنيوتن أبدًا. ومع ذلك، هناك فرق مهم في الفيزياء.

الوزن هو قوة شد الأرض التي تؤثر على الجسم. يعتمد ذلك على المسافة من مركز الأرض. على عكس الوزن، لا تختلف الكتلة باختلاف الموقع. كتلة الجسم هي نفسها على الأرض أو في المدار أو على سطح القمر.

أهداف التعلم:

بنهاية هذا القسم، ستكون قادرًا على:

• شرح الفرق بين الكتلة والوزن
• شرح لماذا لا تكون الأجسام المتساقطة على الأرض في حالة سقوط حر حقًا
• وصف مفهوم انعدام الوزن

وحدات قياس القوة

تُستخدم المعادلة F_net = ma لتحديد صافي القوة (محصلة القوى) من حيث الكتلة والطول والزمن. كما أوضحنا سابقًا، فإن وحدة القوة في النظام الدولي للوحدات هي النيوتن. وحيث أن:

F_net = m.a

فيكون:

1 N = 1 kg · m / s²

أو:

1 نيوتن = 1 كجم × متر / ثانية²

على الرغم من أن العالم بأسره يستخدم النيوتن لوحدة قياس القوة، إلا أن وحدة القوة الأكثر شيوعًا في الولايات المتحدة هي الرطل ويُرمز له بالرمز (lb)، حيث 1 N = 0.225 lb. وهكذا، يزن الشخص الذي يبلغ وزنه 225 رطلاً 1000 نيوتن.

الكتلة والوزن وقوة الجاذبية

عندما يتم إسقاط جسم ما، فإنه يتسارع باتجاه مركز الأرض. ينص قانون نيوتن الثاني على أن القوة الكلية المؤثرة على الجسم مسؤولة عن تسارعه. إذا كانت مقاومة الهواء ضئيلة، فإن القوة الكلية على الجسم الساقط هي قوة الجاذبية، وتسمى عادة وزنه w →، أو قوته بسبب الجاذبية التي تؤثر على جسم كتلته m. يمكن الإشارة إلى الوزن على أنه متجه لأنه يحتوي على اتجاه؛ لأسفل، بحكم التعريف، اتجاه الجاذبية، وبالتالي الوزن هو قوة باتجاه الأسفل. يُشار إلى مقدار الوزن بالرمز w. لعب جاليليو دورًا فعالًا في إظهار أنه في حالة عدم وجود مقاومة للهواء، تسقط جميع الأجسام بنفس التسارع g. باستخدام نتيجة جاليليو وقانون نيوتن الثاني، يمكننا اشتقاق معادلة للوزن.

نفرض أن لدينا جسمًا كتلته m يسقط باتجاه الأرض. إنه يواجه فقط قوة الجاذبية الهابطة، والتي هي الوزن w →. ينص قانون نيوتن الثاني على أن مقدار صافي القوة الخارجية المؤثرة على جسم ما هو: F → _net = m a →. نحن نعلم أن تسارع الجسم بسبب الجاذبية هو g → ، أو → a → = g. بالتعويض عن ذلك في قانون نيوتن الثاني يعطينا المعادلات التالية:

معادلة حساب الوزن

قوة الجاذبية المؤثرة على كتلة هي وزنها. يمكننا كتابة هذا في شكل متجه، حيث w → = الوزن و m الكتلة:

(5.8)

في الشكل القياسي، يمكننا كتابة المعادلة كما يلي:

(5.9)

نظرًا لأن g = 9.80 m / s² على الأرض، فإن وزن جسم تبلغ كتلته 1.00 كجم على الأرض هو 9.8 N، لأن:

تفسير مفهوم الوزن

عندما تكون القوة الخارجية الصافية (المحصلة) على جسم ما هي وزنه، فإننا نقول إنه في حالة سقوط حر، أي القوة الوحيدة المؤثرة على الجسم هي الجاذبية. ومع ذلك، عندما تسقط الأجسام على الأرض لأسفل، فإنها لا تسقط سقوطًا حرًا بشكل مطلق حقًا لأن هناك دائمًا قوة مقاومة تصاعدية من الهواء تؤثر على الجسم.

يختلف التسارع الناتج عن الجاذبية قليلاً فوق سطح الأرض، لذا فإن وزن الجسم يعتمد على موقعه وهذه ليست خاصية جوهرية للجسم. يختلف الوزن بشكل كبير إذا تركنا سطح الأرض. على القمر، على سبيل المثال، التسارع بسبب الجاذبية هو 1.67 متر / ثانية ² فقط. وبالتالي فإن كتلة بمقدار 1.0 كجم سوف تزن 9.8 نيوتن على الأرض وحوالي 1.7 نيوتن فقط على القمر.

التعريف الأوسع للوزن بهذا المعنى هو أن وزن الجسم هو قوة الجاذبية الواقعة عليه من أقرب جسم كبير، مثل الأرض أو القمر أو الشمس. هذا هو التعريف الأكثر شيوعًا وفائدة للوزن في الفيزياء. ومع ذلك، فهو يختلف بشكل كبير عن تعريف الوزن الذي تستخدمه وكالة ناسا ووسائل الإعلام الشعبية فيما يتعلق بالسفر إلى الفضاء والاستكشاف. عندما يتحدثون عن “انعدام الوزن” و”الجاذبية الصغرى”، فإنهم يشيرون إلى الظاهرة التي نسميها “السقوط الحر” في الفيزياء. نستخدم التعريف السابق للوزن، القوة w → الناتجة عن تأثير الجاذبية على جسم كتلته m، ونقوم بالتمييز الدقيق بين السقوط الحر وانعدام الوزن الفعلي.

الفرق بين الكتلة والوزن

اعلم أن الوزن والكتلة كميات فيزيائية مختلفة، على الرغم من ارتباطهما ارتباطًا وثيقًا. الكتلة هي خاصية جوهرية لشيء ما: إنها كمية من المادة. يتم تحديد كمية أو مقدار مادة كائن من خلال عدد الذرات والجزيئات من الأنواع المختلفة التي يحتوي عليها. لأن هذه الأرقام لا تختلف، في الفيزياء النيوتونية، الكتلة لا تختلف؛ لذلك، لا تختلف استجابتها للقوة المؤثرة. في المقابل، الوزن هو قوة الجاذبية التي تؤثر على جسم ما، لذلك فهي تختلف باختلاف الجاذبية. على سبيل المثال، الشخص الأقرب إلى مركز الأرض، على ارتفاع منخفض مثل نيو أورلينز، يزن أكثر بقليل من الشخص الذي يقع في منطقة مرتفعة من دنفر، على الرغم من أنه قد يكون له نفس الكتلة.

من المغري مساواة الكتلة بالوزن، لأن معظم الأمثلة لدينا تحدث على الأرض، حيث يختلف وزن الجسم قليلاً مع اختلاف موقع الجسم. بالإضافة إلى ذلك، إنه صعب حساب وتحديد جميع الذرات والجزيئات في جسم ما، لذلك نادرًا ما يتم تحديد الكتلة بهذه الطريقة. إذا أخذنا في الاعتبار المواقف التي يكون فيها التسارع g → ثابتًا على الأرض، فإننا نرى أن الوزن w → يتناسب طرديًا مع الكتلة m، نظرًا لأن w → = m g →، أي كلما زادت كتلة الجسم، زاد وزنه.

من الناحية العملية، يتم تحديد كتل الأشياء من خلال المقارنة بالكيلوغرام القياسي، كما ناقشنا في الوحدات والقياس. ولكن من خلال مقارنة جسم على الأرض بجسم موجود على سطح القمر، يمكننا أن نرى بسهولة تباينًا في الوزن ولكن ليس في الكتلة. على سبيل المثال، على الأرض، يزن جسم وزنه 5.0 كجم 49 نيوتن؛ على القمر، حيث g تساوي 1.67 m / s²، يزن الجسم 8.4 N. ومع ذلك، لا تزال كتلة الجسم 5.0 كجم على القمر.

مثال 5.8: حساب القوة من الوزن

مزارع يرفع بعض الصخور متوسطة الكثافة من حقل إلى شاحنة. يرفع حجرًا يزن 40.0 رطلاً (حوالي 180 نيوتن). ما القوة التي يستخدمها إذا تسارع الحجر بمعدل 1.5 متر / ثانية ²؟

إستراتيجية الحل

لقد أعطينا وزن الحجر، والذي نستخدمه في إيجاد القوة الكلية على الحجر. ومع ذلك، نحتاج أيضًا إلى معرفة كتلته لتطبيق قانون نيوتن الثاني، لذلك يجب علينا تطبيق معادلة الوزن، w = mg، لتحديد الكتلة.

الحل

لا توجد قوى تعمل في الاتجاه الأفقي، لذلك يمكننا التركيز على القوى الرأسية، كما هو موضح في الرسم البياني التالي للجسم الحر. من الناحية الفنية، فهو ليس جزءًا من مخطط الجسم الحر، ولكنه يساعد في تذكيرنا بأن الجسم يتسارع لأعلى (وبالتالي فإن القوة الكلية تصاعدية).

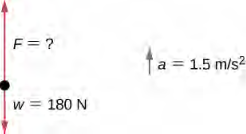
w = mg

m = wg = 180 N / 9.8 m/s² = 18 kg

Σ F = ma

F − w = ma

F − 180 N = (18 kg)(1.5 m/s²)

أي أن:

F − 180 N = 27 N

F = 207 N

الدلالة

لتطبيق قانون نيوتن الثاني كمعادلة أولية في حل مسألة ما، يتعين علينا أحيانًا الاعتماد على معادلات أخرى، مثل المعادلات الخاصة بالوزن أو إحدى معادلات الحركة ضمن موضوعات قوانين نيوتن للحركة بشكل عام، من أجل إكمال الحل.

تأكد من فهمك

بالنسبة إلى المثال 5.8، أوجد التسارع عندما تكون القوة المؤثرة للمزارع 230.0 نيوتن.

المراجع

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022-2023.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.