القوة المعيقة والسرعة الحدية

هناك قوة أخرى مثيرة للاهتمام في الحياة اليومية هي القوة المعيقة على جسم ما عندما يتحرك في مائع fluid (إما غاز gas أو سائل liquid). تشعر بالقوة المعيقة drag force عندما تحرك يدك عبر الماء. قد تشعر بها أيضًا إذا حركت يدك أثناء هبوب رياح قوية. كلما حركت يدك بشكل أسرع، زادت صعوبة تحريكها. تشعر بالقوة المعيقة أقل عندما تميل يدك بحيث يمر الجانب منها فقط عبر الهواء، لقد قللت من مساحة يدك التي تواجه اتجاه الحركة.

أهداف التعلم

بنهاية هذا القسم، ستكون قادرًا على:

  • التعبير عن القوة المعيقة رياضيًا
  • وصف تطبيقات القوة المعيقة
  • تحديد السرعة الحدية
  • تحديد السرعة الحدية لجسم بمعلومية كتلته

القوة المعيقة

مثل الاحتكاك، فإن القوة المعيقة دائمًا تعارض حركة الجسم. على عكس الاحتكاك البسيط، تتناسب القوة المعيقة مع بعض وظائف سرعة الجسم في ذلك السائل. هذه الوظيفة معقدة وتعتمد على شكل الجسم، وحجمه، وسرعته، والسوائل الموجودة فيه. بالنسبة لمعظم الأجسام الكبيرة مثل راكبي الدراجات والسيارات والكرات القاعدية، لا تتحرك ببطء شديد، حجم القوة المعيقة FD تتناسب طرديًا مع مربع سرعة الجسم. يمكننا كتابة هذه العلاقة رياضيًا كما يلي:

FD ∝ v2

عند الأخذ بعين الاعتبار العوامل الأخرى، تصبح هذه العلاقة:

FD=12CρAv2,FD=12CρAv2,

(6.5)

حيث C هي معامل الإعاقة، وA هي مساحة الجسم التي تواجه السائل، وρ هي كثافة السائل. (تذكر أن الكثافة هي الكتلة لكل وحدة حجم، أي الكتلة قسمة الحجم). يمكن أيضًا كتابة هذه المعادلة بطريقة أكثر عمومية مثل:

FD=b vn

حيث b ثابت مكافئ لـ: 1/2CρA

لقد قمنا بتعيين الأس n لهذه المعادلات على القيمة 2 لأنه عندما يتحرك جسم ما بسرعة عالية في الهواء، فإن مقدار القوة المعيقة تتناسب مع مربع السرعة. كما سنرى في ميكانيكا الموائع، بالنسبة للجسيمات الصغيرة التي تتحرك بسرعات منخفضة في سائل ما، فإن الأس n يساوي 1.

معادلة القوة المعيقة

القوة المعيقة FD تتناسب مع مربع سرعة الجسم. رياضيًا يكون:

FD=12CρAv2,FD=12CρAv2,

حيث C هي معامل الإعاقة، وA هي مساحة الجسم التي تواجه المائع، وρ هي كثافة السائل.

يسعى الرياضيون ومصممي السيارات إلى تقليل القوة المعيقة لتقليل أوقات السباق (الشكل 6.29). يمكن للتشكيل الديناميكي الهوائي للسيارة أن يقلل من القوة المعيقة وبالتالي يزيد من المسافة المقطوعة بالغاز في السيارة.

الشكل 6.29: من سيارات السباق إلى المتسابقين المزلجين، يعد التشكيل الديناميكي الهوائي أمرًا بالغ الأهمية لتحقيق سرعات قصوى. تم تصميم الزلاجات للسرعة وهي على شكل رصاصة ذات زعانف مدببة. (المصدر: الجيش الأمريكي – ويكيميديا ​​كومنز).

يتم تحديد قيمة معامل الإعاقة C تجريبيًا، عادةً باستخدام نفق الرياح (الشكل 6.30).

القوة المعيقة والسرعة الحدية

صورة لطائرة نموذجية في نفق هوائي.

الشكل 6.30: يختبر باحثو ناسا نموذج طائرة في نفق هوائي. (المصدر: وكالة ناسا)

يمكن أن يعتمد معامل الإعاقة على السرعة، لكننا نفترض أنها ثابتة هنا. يسرد الجدول 6.2 بعض معاملات الإعاقة النموذجية لمجموعة متنوعة من الكائنات. لاحظ أن معامل الإعاقة هو كمية بلا أبعاد أي بلا وحدات قياس بل مجرد قيمة عددية.

بسرعات الطرق السريعة، أكثر50% من قوة السيارة هي للتغلب على إعاقة الهواء. تبلغ سرعة الانطلاق الأكثر كفاءة في استهلاك الوقود حوالي 70-80 كم/ساعة (حوالي 45-50 ميل / ساعة). لهذا السبب، خلال أزمة النفط في السبعينيات في الولايات المتحدة، تم ضبط السرعات القصوى على الطرق السريعة عند حوالي 90 كم/ ساعة (55 ميل / ساعة).

الشيءمعامل الإعاقة C
Airfoil0.05
Toyota Camry0.28
Ford Focus0.32
Honda Civic0.36
Ferrari Testarossa0.37
Dodge Ram Pickup0.43
Sphere0.45
Hummer H2 SUV0.64
Skydiver (feet first)0.70
Bicycle0.90
Skydiver (horizontal)1.0
Circular flat plate1.12
جدول 6.2: القيم النموذجية لمعامل الإعاقة C

يجري بحث كبير في عالم الرياضة لتقليل الإعاقة. يتم إعادة تصميم الدمامل الموجودة على كرات الجولف، وكذلك الملابس التي يرتديها الرياضيون. يرتدي المتسابقون على الدراجات وبعض السباحين والعدائين بدلات داخلية كاملة. ارتدت الأسترالية كاثي فريمان بدلة كاملة للجسم في أولمبياد سيدني 2000 وفازت بميدالية ذهبية في سباق 400 متر. ارتدى العديد من السباحين في أولمبياد بكين 2008 بدلات (سبيدو). ربما أحدثت فرقًا في تحطيم العديد من الأرقام القياسية العالمية (الشكل 6.31). يحلق معظم السباحين (وراكبي الدراجات) شعر الجسم. يمكن أن يكون لمثل هذه الابتكارات تأثير قطع أجزاء من الألف من الثانية في السباق، مما يحدث فرقًا في بعض الأحيان بين الميدالية الذهبية والميدالية الفضية. إحدى النتائج هي أنه يجب تطوير إرشادات مهمة ودقيقة وباستمرار للحفاظ على سلامة الرياضة.

صورة لثلاثة سباحين يرتدون بدلات.

صورة لثلاثة سباحين يرتدون بدلات.

شكل 6.31: بدلات الجسم، مثل بدلة LZR Racer، تم تسجيلها في المساعدة في العديد من الأرقام القياسية العالمية بعد إصدارها في عام 2008. يوفر “الجلد” الأكثر نعومة والمزيد من قوى الضغط على جسم السباح على الأقل 10% إعاقة أقل. (المصدر: وكالة ناسا / كاثي بارنستورف)

السرعة الحدية

تحدث بعض المواقف المثيرة للاهتمام المرتبطة بقانون نيوتن الثاني عند النظر في تأثيرات القوى المعيقة على جسم متحرك. على سبيل المثال، ضع في اعتبارك أن لاعب القفز بالمظلات يسقط في الهواء تحت تأثير الجاذبية. القوتان المؤثرتان عليه هما قوة الجاذبية والقوة المعيقة (تجاهل قوة الطفو الصغيرة). تظل قوة الجاذبية الهابطة ثابتة بغض النظر عن السرعة التي يتحرك بها الشخص. ومع ذلك، مع زيادة سرعة الشخص، يزداد مقدار القوة المعيقة حتى يصبح مقدار القوة المعيقة مساويًا لقوة الجاذبية، مما ينتج عنه صافي قوة مقدارها صفر. تعني القوة الصافية الصفرية أنه لا يوجد تسارع، كما هو موضح في قانون نيوتن الثاني. في هذه المرحلة، تظل سرعة الشخص ثابتة ونقول إن الشخص قد وصل إلى سرعته الحدية Terminal Velocity (أو النهائية القصوى) VT.

حيث أن القوة المعيقة FD تتناسب مع مربع السرعة، يجب أن يتحرك لاعب القفز المظلي الأثقل بسرعة أكبر حتى تتساوى القوة المعيقة FD مع وزنه. دعونا نرى كيف يعمل هذا من الناحية الكمية.

عند الوصول إلى السرعة الحدية يكون:

Fnet=mg − FD = ma = 0

وهكذا يكون:

m g = FD

باستخدام معادلة القوة المعيقة، لدينا:

mg=12CρAvT2.mg=12CρAvT2.

نحل المعادلة لإيجاد السرعة:

vT=2mgρCA.vT=2mgρCA.

افترض أن كثافة الهواء هي ρ = 1.21 كجم/ م3.

تبلغ مساحة المقطع العرضي للقافز المظلي الذي يبلغ وزنه 75 كجم تقريبًا A هي 0.18 متر مربع، ومعامل الإعاقة تقريبًا هو 0.70، من ذلك نجد أن:

vT=2(75kg)(9.80m/s2)(1.21kg/m3)(0.70)(0.18m2)=98m/s=350km/h.vT=2(75kg)(9.80m/s2)(1.21kg/m3)(0.70)(0.18m2)=98m/s=350km/h.

هذا يعني أن لاعب القفز بالمظلات بكتلة 75 كجم يحقق سرعة حدية تبلغ حوالي 350 كم / ساعة أثناء السفر في وضع الرأس أولاً، مما يقلل من المساحة والقوة المعيقة. في وضع النسر المنتشر، قد تنخفض السرعة الحدية إلى حوالي 200 كم / ساعة مع زيادة المساحة. تصبح هذه السرعة الحدية أصغر بكثير بعد فتح المظلة.

مثال 6.17: السرعة الحدية للاعب القفز بالمظلات

أوجد السرعة الحدية لقافز مظلي وزنه 85 كجم يسقط في وضع النسر المنتشر. افترض أنه في وضع النسر المنتشر، يكون للقافز مساحة مقطعية تبلغ0.70م2.

استراتيجية الحل

عند السرعة الحدية، يكون صافي القوة FNet = صفر.

وبالتالي، فإن القوة المعيقة المؤثرة على اللاعب يجب أن تساوي قوة الجاذبية (وزن الشخص). باستخدام معادلة القوة المعيقة، نجد أن:

mg=12ρCAv2.mg=12ρCAv2.

الحل

السرعة الحدية VT يمكن كتابتها كما يلي:

vT=2mgρCA=2(85kg)(9.80m/s2)(1.21kg/m3)(1.0)(0.70m2)=44m/s.vT=2mgρCA=2(85kg)(9.80m/s2)(1.21kg/m3)(1.0)(0.70m2)=44m/s.

الدلالة

هذه النتيجة متوافقة مع قيمة السرعة الحدية المذكورة مسبقًا. كان للاعب القفز بالمظلات الذي يبلغ وزنه 75 كجم والذي يتحرك بأقدامه أولًا سرعة حدية تبلغ = 98 م / ث. كان وزنه أقل ولكن المساحة الأمامية أصغر وبالتالي كانت الإعاقة بسبب الهواء أقل.

تحقق من فهمك 6.10

أوجد السرعة النهائية لقافز مظلي وزنه 50 كجم يسقط بطريقة النسر المنتشر.

العلاقة بين السرعة الحدية والحجم

يقدم حجم الجسم الذي يسقط في الهواء تطبيقًا آخر مثيرًا للاهتمام لقوة إعاقة الهواء. إذا سقطت من فرع شجرة ارتفاعه 5 أمتار، فمن المحتمل أن تتأذى – وربما تتكسر العظام. ومع ذلك، فإن سنجاب صغير يفعل هذا طوال الوقت دون أن يصاب بأذى. أنت لا تصل إلى سرعة حدية في مثل هذه المسافة القصيرة، لكن السنجاب يصل إليها.

الاقتباس التالي المثير للاهتمام حول حجم الحيوان والسرعة الحدية مأخوذ من مقال كتبه عالم الأحياء البريطاني جيه بي إس هالدين عام 1928 بعنوان “في الحجم المناسب”.

“بالنسبة للفأر وأي حيوان أصغر، فإن [الجاذبية] لا تمثل عمليًا أي مخاطر. يمكنك إسقاط الفأر أسفل منجم بطول ألف ياردة؛ وعند وصوله إلى القاع، يتعرض لصدمة خفيفة ويبتعد، بشرط أن تكون الأرض ناعمة إلى حد ما. يقتل فأر، ويتحطم الرجل، ويتناثر الحصان. لأن المقاومة المقدمة للحركة بواسطة الهواء تتناسب مع سطح الجسم المتحرك. اقسم طول الحيوان وعرضه وارتفاعه على عشرة؛ ينخفض ​​وزنه إلى جزء من الألف، لكن سطحه لا ينخفض بقيمة تتجاوز المائة. لذا فإن مقاومة السقوط في حالة الحيوان الصغير أكبر نسبيًا بعشر مرات من القوة المعيقة”.

لا يصمد الاعتماد التربيعي الموضح أعلاه لإعاقة الهواء على السرعة إذا كان الجسم صغيرًا جدًا، أو يسير ببطء شديد، أو في وسط أكثر كثافة من الهواء. لذا نجد أن القوة المعيقة تتناسب طرديًا مع السرعة فقط. هذه العلاقة مقدمة من قانون ستوكس.

قانون ستوكس

بالنسبة لجسم كروي يسقط في وسط، فإن القوة المعيقة تساوي:

Fs = 6 π r η v

(6.6)

حيث r هو نصف قطر الجسم، η هي لزوجة السائل، و v هي سرعة الجسم.

تقدم الكائنات الحية الدقيقة وحبوب اللقاح وجزيئات الغبار أمثلة جيدة على قانون ستوكس. نظرًا لأن كل من هذه الأجسام صغيرة جدًا، نجد أن العديد من هذه الأجسام تتحرك دون مساعدة إلا بسرعة ثابتة (سرعة حدية). السرعات الحدية للبكتيريا (الحجم حوالي1ميكرومتر ) يمكن أن تكون حوالي 2 مايكرومتر / ثانية.

للتحرك بسرعة أكبر، تسبح العديد من البكتيريا باستخدام سوط (عضيّات على شكل ذيول صغيرة) تعمل بمحركات صغيرة مدمجة في الخلية.

يمكن أن تتحرك الرواسب في البحيرة بسرعة حدية أكبر (حوالي5 مايكرومتر / ثانية)، لذلك قد يستغرق الأمر أيامًا حتى يصل إلى قاع البحيرة بعد ترسبه على السطح.

إذا قارنا الحيوانات التي تعيش على الأرض بتلك الموجودة في الماء، يمكنك أن ترى كيف أثرت القوة المعيقة على التطور. يتم تنظيم الأسماك والدلافين وحتى الحيتان الضخمة في الشكل لتقليل القوى المعيقة. الطيور منبسطة والأنواع المهاجرة التي تطير لمسافات طويلة غالبًا ما يكون لها سمات خاصة مثل الأعناق الطويلة. سرب الطيور يطير على شكل رأس حربة حيث يشكل السرب نمطًا انسيابيًا (الشكل 6.32). في البشر، أحد الأمثلة المهمة على التبسيط هو شكل الحيوانات المنوية، والتي يجب أن تكون فعالة في استخدامها للطاقة.

صورة لإوز يطير في شكل V.

الشكل 6.32: الأوز يطير في تكوين حرف V أثناء رحلات الهجرة الطويلة. يقلل هذا الشكل من القوة المعيقة واستهلاك الطاقة للطيور الفردية، كما يتيح لهم طريقة أفضل للتواصل. (المصدر: تعديل العمل بواسطة Julo / ويكيميديا ​​كومنز)

تعليم تفاعلي

في عروض المحاضرات، نقوم بقياسات القوة المعيقة على كائنات مختلفة. يتم وضع الأشياء في تيار هواء موحد تم إنشاؤه بواسطة مروحة. احسب معامل السحب.

حساب قوى الاحتكاك المعتمدة على السرعة

عندما ينزلق جسم على سطح ما، تكون قوة الاحتكاك عليه ثابتة تقريبًا وتعطى بواسطة μkN.

لسوء الحظ، فإن قوة الاحتكاك المؤثرة على جسم يتحرك عبر سائل أو غاز لا تتصرف بهذه البساطة. القوة المعيقة هذه بشكل عام هي دالة معقدة لسرعة الجسم. ومع ذلك، بالنسبة لجسم يتحرك في خط مستقيم بسرعات معتدلة عبر سائل مثل الماء، يمكن في كثير من الأحيان تقريب قوة الاحتكاك بواسطة: fR=−b v.

حيث b ثابت تعتمد قيمته على أبعاد وشكل الجسم وخصائص السائل، و v هي سرعة الجسم. حالتان يمكن أن تمثلهما هذه المعادلة لقوة الاحتكاك وهما زورق آلي يتحرك عبر الماء وجسم صغير يسقط ببطء عبر سائل.

لنفكر في سقوط الجسم عبر سائل. يوضح الشكل 6.33 مخطط الجسم الحر لهذا الكائن مع الاتجاه الموجب لأسفل. يعطي قانون نيوتن الثاني في الاتجاه الرأسي المعادلة التفاضلية التالية:

mg−bv=mdvdt,mg−bv=mdvdt,

mg – bv = m dv/dt

حيث كتبنا التسارع كدالة dv/dt. ومع زيادة v، تزداد قوة الاحتكاك -bv حتى تتطابق مع mg. في هذه المرحلة، لا يوجد تسارع وتظل السرعة ثابتة عند السرعة الحدية VT.

من المعادلة السابقة،

m g− b vT = 0

لذا ينتج أن:

vT=mgb.vT=mgb.

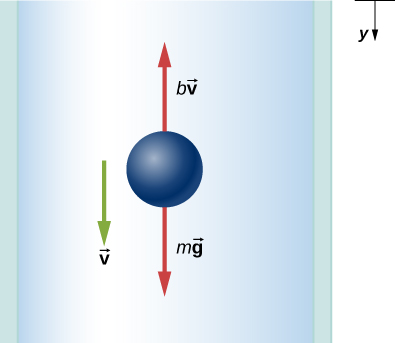
الشكل 6.33: رسم تخطيطي للجسم الحر لجسم يسقط عبر وسط مقاوم.

يُظهر مخطط الجسم الحر القوى m مضروبة في المتجه g التي تشير عموديًا إلى الأسفل و b في المتجه v متجهًا عموديًا لأعلى. السرعة، المتجه v، عموديًا لأسفل. الاتجاه الموجب y هو أيضًا عموديًا لأسفل.

يمكننا إيجاد سرعة الجسم عن طريق إجراء التكامل للمعادلة التفاضلية لـ v. أولاً، نعيد ترتيب الحدود في هذه المعادلة للحصول على ما يلي:

dvg−(b/m)v=dt.dvg−(b/m)v=dt.

dv/(g−b/m)v)=dt.

افترض أن السرعة V=0، عند الزمن t=0، ينتج عن تكامل هذه المعادلة أن:

∫0vdv′g−(b/m)v′=∫0tdt′,∫0vdv′g−(b/m)v′=∫0tdt′,

أو:

−mbln(g−bmv′)|0v=t′|0t,−mbln(g−bmv′)|0v=t′|0t,

حيث v’ و t’ هي متغيرات وهمية للتكامل. مع الحدود المعطاة، نجد أن:

−mb[ln(g−bmv)−lng]=t.−mb[ln(g−bmv)−lng]=t.

وحيث أن:

lnA−lnB=ln(A/B)

ولأن: ln(A/B)=x يؤدي إلى أن يكون: ex=A/B

نحصل على:

g−(bv/m)g=e−bt/m,g−(bv/m)g=e−bt/m,

وبالتالي:

v=mgb(1−e−bt/m).v=mgb(1−e−bt/m).

لاحظ أن كلما اقترب الزمن t→∞  فإن السرعة v→mg/b=vT، وهي السرعة الحدية.

يمكن العثور على الموضع في أي وقت من خلال إجراء تكامل المعادلة بالنسبة لـ v. مع: v=dy/dt.

dy=mgb(1−e−bt/m)dt.dy=mgb(1−e−bt/m)dt.

dy=mgb(1−e−bt/m)dt

بفرض أن y=0 عندما t=0:

∫0ydy′=mgb∫0t(1−e−bt‘/m)dt′,∫0ydy′=mgb∫0t(1−e−bt‘/m)dt′,

والتي تعطي النتيجة التالية:

y=mgbt+m2gb2(e−bt/m−1).y=mgbt+m2gb2(e−bt/m−1).

مثال 6.18: تأثير القوة المقاومة على زورق آلي

يتحرك زورق آلي عبر بحيرة بسرعة v0 عندما تجمد محركه فجأة وتوقف. ثم يتباطأ القارب تحت قوة الاحتكاك FR = −bv. (أ) ما هي سرعة القارب وموقعه كدالة في الزمن؟ (ب) إذا تباطأ القارب من 4.0 إلى 1.0 م / ث في 10 ثوانٍ، فما المسافة التي يقطعها قبل التوقف؟

الحل

(أ) مع توقف المحرك، القوة الأفقية الوحيدة المؤثرة على القارب هي FR = −bv

لذلك من قانون نيوتن الثاني، يكون:

mdvdt=−bv,mdvdt=−bv,

والتي يمكن أن نكتبها كما يلي:

dvv=−bmdt.dvv=−bmdt.

بإجراء التكامل لهذه المعادلة بين الزمن صفر عندما تكون السرعة V0 والزمن t عندما تكون السرعة V، يكون لدينا:

∫0vdv′v′=−bm∫0tdt′.∫0vdv′v′=−bm∫0tdt′.

وهكذا، يكون:

lnvv0=−bmt,lnvv0=−bmt,

ويمكننا كتابة هذا على شكل:

v=v0e−bt/m.v=v0e−bt/m.

الآن من تعريف السرعة، يكون:

dxdt=v0e−bt/m,dxdt=v0e−bt/m,

إذن، لدينا:

dx=v0e−bt/mdt.dx=v0e−bt/mdt.

مع الموضع الأولي صفر، يكون لدينا:

∫0xdx‘=v0∫0te−bt‘/mdt‘,∫0xdx‘=v0∫0te−bt‘/mdt‘,

وكذلك:

x=−mv0be−bt‘/m|0t=mv0b(1−e−bt/m).x=−mv0be−bt‘/m|0t=mv0b(1−e−bt/m).

ومع مرور الوقت، تقترب e−bt/m→0

ويقترب موضع القارب من القيمة النهائية:

xmax=mv0b.xmax=mv0b.

على الرغم من أن هذا يخبرنا أن القارب يستغرق وقتًا غير محدود للوصول إلى القيمة X max، توقف القارب بشكل فعال بعد فترة زمنية معقولة. على سبيل المثال، عند: t=10 m/b.

لدينا:

v=v0e−10≃4.5×10−5v0,v=v0e−10≃4.5×10−5v0,

وكذلك لدينا أيضًا:

x=xmax(1−e−10)≃0.99995xmax.x=xmax(1−e−10)≃0.99995xmax.

لذلك، وصلت سرعة القارب وموقعه بشكل أساسي إلى قيمهما النهائية.

(ب)

مع v0=4 m/s وv=1 m/s، يكون لدينا:

1.0m/s=(4.0m/s)e−(b/m)(10s),1.0m/s=(4.0m/s)e−(b/m)(10s),

لذا، يكون:

ln0.25=−ln4.0=−bm(10s),ln0.25=−ln4.0=−bm(10s),

وبالتالي يكون:

bm=110ln4.0s-1=0.14s-1.bm=110ln4.0s-1=0.14s-1.

الآن وضع القارب النهائي:

xmax=mv0b=4.0m/s0.14s−1=29m.xmax=mv0b=4.0m/s0.14s−1=29m.

الدلالة

في كلا المثالين السابقين وجدنا قيم “نهائية”. السرعة الحدية هي نفسها السرعة النهائية، وهي سرعة الجسم الساقط بعد مرور فترة طويلة (نسبيًا). وبالمثل، فإن المسافة النهائية للقارب هي المسافة التي سيقطعها القارب بعد مرور فترة طويلة من الوقت. نظرًا لخصائص الاضمحلال الأسي، فإن الوقت الذي يستغرقه الوصول إلى أي من هذه القيم ليس طويلاً في الواقع (بالتأكيد ليس مقدارًا غير محدود من الوقت!) ولكن يتم إيجاده بسرعة عن طريق أخذ الحد إلى اللانهاية.

تحقق من فهمك 6.11

افترض أنه يمكن تقريب قوة مقاومة الهواء على لاعب القفز بالمظلات بالمعادلة: f=-bv2. إذا كانت السرعة النهائية لقافز مظلي وزنه 100 كجم تساوي 60 م / ث، فما قيمة b؟

المراجع

  • موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
  • كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.
error:
Scroll to Top