الطاقة الكامنة وحفظ الطاقة

الشكل 8.1: الموضح هنا هو جزء من تمثال لآلة الكرة لجورج رودس. يتم رفع الكرة في هذه الأداة الغريبة، وتدحرجها، وتسقطها، وترتد، وتصطدم بأشياء مختلفة، ولكن خلال رحلاتها، تتغير طاقتها الحركية بكميات محددة يمكن التنبؤ بها، والتي تعتمد على موقعها والأشياء التي تتفاعل معها. الطاقة الكامنة وحفظ الطاقة (الائتمان: تعديل العمل بواسطة Roland Tanglao)

مخطط الفصل

8.1 الطاقة الكامنة للنظام
8.2 القوات المحافظة وغير المحافظة
8.3 الحفاظ على الطاقة
8.4 مخططات الطاقة المحتملة والاستقرار
8.5 مصادر الطاقة

في منحوتة الكرة المتدحرجة لجورج رودز، يحكم مبدأ الحفاظ على الطاقة التغيرات في الطاقة الحركية للكرة ويربطها بالتغييرات والتحويلات لأنواع أخرى من الطاقة المرتبطة بتفاعلات الكرة. في هذا الفصل، نقدم المفهوم المهم للطاقة الكامنة Potential Energy. سيمكننا ذلك من صياغة قانون حفظ الطاقة الميكانيكية وتطبيقه على الأنظمة البسيطة، مما يجعل حل المسائل أسهل. في القسم الأخير حول مصادر الطاقة، سننظر في عمليات نقل الطاقة والقانون العام لحفظ على الطاقة. خلال هذا الكتاب، سيتم تطبيق قانون حفظ الطاقة بمزيد من التفصيل بشكل متزايد، حيث تواجه أنظمة أكثر تعقيدًا وتنوعًا وأشكالًا أخرى من الطاقة.

المحتويات

الطاقة الكامنة للنظام

أهداف التعلم

بنهاية هذا القسم، ستكون قادرًا على:

ربط فرق الطاقة الكامنة بالشغل المبذول على جسيم لنظام بدون احتكاك أو سحب هوائي
شرح معنى أن تكون دالة الطاقة الكامنة للنظام تساوي صفر
حساب وتطبيق طاقة الجاذبية الكامنة لجسم قريب من سطح الأرض والطاقة الكامنة المرنة لنظام كتلة الزنبرك

في موضوع الشغل، رأينا أن الشغل المبذول على جسم بواسطة قوة الجاذبية الثابتة، بالقرب من سطح الأرض، على أي إزاحة هو دالة فقط للاختلاف في مواضع نقاط النهاية للإزاحة. تسمح لنا هذه الخاصية بتعريف نوع مختلف من الطاقة للنظام عن طاقته الحركية، والتي تسمى الطاقة الكامنة Potential Energy. نأخذ في الاعتبار خصائص وأنواع مختلفة من الطاقة الكامنة في الأقسام الفرعية التالية.

أساسيات الطاقة الكامنة

في الحركة ثنائية وثلاثية الأبعاد، قمنا بتحليل حركة المقذوف، مثل ركل كرة القدم في الشكل 8.2. في هذا المثال، دعنا نتجاهل الاحتكاك ومقاومة الهواء ونبدأ التحليل فورًا بعد الركلة، في بداية حركة الكرة المقذوفة. مع ارتفاع كرة القدم، يكون الشغل الذي تقوم به قوة الجاذبية على كرة القدم سالبًا، لأن إزاحة الكرة موجبة رأسيًا والقوة الناتجة عن الجاذبية سالبة رأسيًا. لاحظنا أيضًا أن الكرة تباطأت حتى وصلت إلى أعلى نقطة لها في الحركة، مما قلل من الطاقة الحركية للكرة. يترجم هذا الخسارة في الطاقة الحركية إلى زيادة في طاقة الجاذبية الكامنة لنظام كرة القدم والأرض.

عندما تسقط كرة القدم نحو الأرض، فإن الشغل المبذول على كرة القدم أصبح الآن إيجابيًا، لأن الإزاحة وقوة الجاذبية كلاهما يتجهان عموديًا إلى الأسفل. تتسارع الكرة أيضًا، مما يشير إلى زيادة الطاقة الحركية. لذلك، يتم تحويل الطاقة من طاقة الجاذبية الكامنة إلى طاقة حركية.

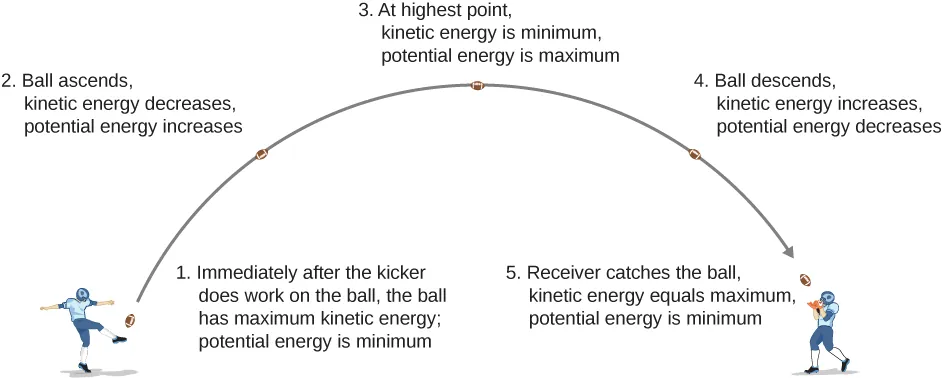
الشكل 8.2: عندما تبدأ كرة القدم في الهبوط نحو المستقبل الواسع، يتم تحويل طاقة وضع الجاذبية مرة أخرى إلى طاقة حركية.

بناءً على هذا السيناريو ، يمكننا تحديد فرق الطاقة الكامنة من النقطة A إلى النقطة B على أنها سلبية الشغل المنجز:

Δ U_{A B} = U_{B} - U_{A} = − W_{A B} .

8.1

تنص هذه الصيغة صراحة على فرق الطاقة الكامنة، وليس مجرد طاقة كامنة مطلقة. لذلك، نحتاج إلى تحديد الطاقة الكامنة في موضع معين بطريقة توضح القيم القياسية للطاقة الكامنة من تلقاء نفسها، بدلاً من اختلافات الطاقة المحتملة. نقوم بذلك عن طريق إعادة كتابة دالة الطاقة الكامنة بدلالة ثابت عشوائي:

Δ U = U (\vec{r}) - U ({\vec{r}}_{0}) .

8.2

اختيار الطاقة الكامنة في موقع البداية r₀يتم بدافع الملاءمة في المسألة المعينة. والأهم من ذلك، يجب ذكر أي خيار يتم اتخاذه والحفاظ عليه متسقًا طوال المشكلة المحددة. هناك بعض الخيارات المقبولة جيدًا للطاقة الكامنة الأولية. على سبيل المثال، يُعرَّف أدنى ارتفاع في مشكلة ما على أنه صفر طاقة محتملة، أو إذا كان الجسم موجودًا في الفضاء، فغالبًا ما يتم تعريف أبعد نقطة بعيدة عن النظام على أنها صفر طاقة كامنة. ثم الطاقة الكامنة بالنسبة للصفر عند r₀ أنه ببساطة U(r).

طالما لا يوجد احتكاك أو مقاومة للهواء، فإن التغير في الطاقة الحركية لكرة القدم يساوي التغير في الطاقة الكامنة للجاذبية في كرة القدم. يمكن تعميم هذا على أي طاقة كامنة:

Δ K_{A B} = - Δ U_{A B} .

8.3

لنلق نظرة على مثال محدد، نختار صفر طاقة وضع لطاقة وضع الجاذبية عند نقاط ملائمة.

مثال 8.1: الخصائص الأساسية للطاقة الكامنة

يتحرك جسيم على طول المحور السيني تحت تأثير قوة معطاة حسب المعادلة F = −ax²حيث a = 3 N/m².

(أ) ما هو الفرق في طاقتها الكامنة أثناء تحركها من x_A = 1 m إلى x_B = 2m. (ب) ما هي الطاقة الكامنة للجسيم عند x=1m مع الأخذ بالاعتبار أن مقدار 0.5 جول من الطاقة الكامنة يتوفر عند x=0؟

استراتيجية الحل

(أ) الفرق في الطاقة الكامنة هو سالب الشغل المبذول، كما هو محدد في المعادلة 8.1. تم تعريف الشغل في الفصل السابق على أنه حاصل الضرب النقطي للقوة مع المسافة. نظرًا لأن الجسيم يتحرك للأمام في الاتجاه x، فإن حاصل الضرب النقطي يبسط إلى الضرب: iˆ⋅iˆ=1.

لإيجاد إجمالي الشغل المبذول، علينا إجراء تكامل للدالة للفترة بين الحدين المعينين. بعد التكامل، يمكننا تحديد الشغل أو التغيير في الطاقة الكامنة. (ب) دالة الطاقة الكامنة، بالنسبة للصفر عند x=0 هو التكامل غير المحدد الذي تمت مواجهته في الجزء (أ)، مع ثابت التكامل المحدد من المعادلة 8.3. ثم نقوم بالتعويض بقيمة x في دالة الطاقة الكامنة لحساب الطاقة الكامنة عند x=1 m.

الحل

(أ) الشغل المبذول بواسطة القوة المعطاة أثناء تحرك الجسيم من إحداثيات x إلى x + dx في بعد واحد:

d W = \vec{F} \cdot d \vec{r} = F d x = − a x^{2} d x .

بالتعويض عن هذا التعبير في المعادلة 8.1، نحصل على:

Δ U = − W = \int_{x_{1}}^{x_{2}} a x^{2} d x = \frac{1}{3} (3 {N/m}^{2}) {x^{3} |}_{1 m}^{2 m} = 7 J .

(ب) التكامل غير المحدود لوظيفة الطاقة الكامنة في الجزء (أ) هو:

U (x) = \frac{1}{3} a x^{3} + const .,

ونريد أن يتم تحديد الثابت بواسطة:

U (0) = 0.5 J .

وبالتالي، الطاقة الكامنة بالنسبة للصفر عند x=0 هي ببساطة:

U (x) = \frac{1}{3} a x^{3} + 0.5 J .

لذلك، الطاقة الكامنة عند x=1 m تكون:

U (1 m) = \frac{1}{3} (3 {N/m}^{2}) {(1 m)}^{3} + 0.5 J = 1.5 J .

الدلالة

في هذا المثال أحادي البعد، أي دالة يمكننا إجراء التكامل لها، بغض النظر عن المسار، تكون متحفظة. لاحظ كيف طبقنا تعريف فرق الطاقة الكامنة لتحديد دالة الطاقة الكامنة فيما يتعلق بالصفر عند نقطة مختارة. لاحظ أيضًا أن الطاقة الكامنة، كما هو محدد في الجزء (ب)، عند x=1m هي U(1m)=1 وعند x=2m هي U(2m)=8؛ والفرق بينهما هو النتيجة في الجزء (أ).

تحقق من فهمك 8.1

في المثال 8.1، ما هي الطاقات الكامنة للجسيم عند x=1m وعند x=2m، إذا كانت بالنسبة للصفر عند x=1.5m. تحقق من أن فرق الطاقة الكامنة لا يزال 7 جول.

أنظمة من عدة جسيمات

بشكل عام، يمكن أن يتكون نظام الاهتمام من عدة جسيمات. الفرق في الطاقة الكامنة للنظام هو سالب الشغل الذي تقوم به قوى الجاذبية أو القوى المرنة، والتي، كما سنرى في القسم التالي، قوى محافظة. يعتمد فرق الطاقة الكامنة فقط على المواضع الأولية والنهائية للجسيمات، وعلى بعض المعلمات التي تميز التفاعل (مثل كتلة الجاذبية أو ثابت الزنبرك لقوة قانون هوك).

من المهم أن نتذكر أن الطاقة الكامنة هي خاصية للتفاعلات بين الكائنات في نظام مختار، وليست مجرد خاصية لكل كائن. ينطبق هذا بشكل خاص على القوى الكهربائية، على الرغم من أنه في أمثلة الطاقة الكامنة التي نعتبرها أدناه، فإن أجزاء من النظام إما كبيرة جدًا (مثل الأرض، مقارنة بجسم على سطحها) أو صغيرة جدًا (مثل الزنبرك عديم الكتلة)، والتغييرات التي تخضع لها تلك الأجزاء لا تذكر عند تضمينها في النظام.

أنواع الطاقة الكامنة

لكل نوع من أنواع التفاعل الموجودة في النظام، يمكنك تسمية نوع مطابق من الطاقة الكامنة. إجمالي الطاقة الكامنة للنظام هو مجموع الطاقات الكامنة لجميع الأنواع. (يأتي هذا من الخاصية المضافة لحاصل الضرب القياسي (النقطي) في تعبير الشغل المبذول). لنلقِ نظرة على بعض الأمثلة المحددة لأنواع الطاقة الكامنة التي تمت مناقشتها في موضوع الشغل. أولاً، نأخذ في الاعتبار كل من هذه القوى عند العمل معها بشكل منفصل، ثم عندما يعمل كلاهما معًا.

طاقة وضع الجاذبية بالقرب من سطح الأرض

يتكون نظام الاهتمام من كوكبنا والأرض وجسيم واحد أو أكثر بالقرب من سطحه (أو أجسام صغيرة بما يكفي لاعتبارها جسيمات، مقارنة بالأرض). قوة الجاذبية على كل جسيم (أو جسم) هي فقط وزنه mg بالقرب من سطح الأرض، ويعمل عموديًا لأسفل. وفقًا لقانون نيوتن الثالث، يمارس كل جسيم قوة على الأرض متساوية الحجم ولكن في الاتجاه المعاكس. يخبرنا قانون نيوتن الثاني أن مقدار التسارع الناتج عن كل من هذه القوى على الأرض هو mg مقسومة على كتلة الأرض. نظرًا لأن نسبة كتلة أي جسم عادي إلى كتلة الأرض صغيرة جدًا، يمكن إهمال حركة الأرض تمامًا. لذلك، نعتبر هذا النظام مجموعة من أنظمة الجسيمات المفردة، تخضع لقوة الجاذبية المنتظمة للأرض.

في الشغل، الشغل المبذول على جسم بواسطة قوة الجاذبية المنتظمة للأرض، بالقرب من سطحها، يعتمد على كتلة الجسم، والتسارع بسبب الجاذبية، والاختلاف في الارتفاع الذي اجتازه الجسم، كما هو موضح في المعادلة 7.4. بالتعريف، هذا الشغل هو سالب الفرق في طاقة وضع الجاذبية، لذلك هذا الاختلاف هو:

Δ U_{grav} = − W_{grav, A B} = m g (y_{B} - y_{A}) .

8.4

يمكنك أن ترى من هذا أن دالة طاقة وضع الجاذبية، بالقرب من سطح الأرض، هي:

U (y) = m g y + const .

8.5

يمكنك اختيار قيمة الثابت، كما هو موضح في مناقشة المعادلة 8.2؛ ومع ذلك، لحل معظم المسائل، فإن الثابت الأكثر ملاءمة للاختيار هو y=0 ، وهو أدنى موضع رأسي في المسألة.

مثال 8.2: طاقة الجاذبية الكامنة للمتنزه

تقع قمة Great Blue Hill في ميلتون، ماساتشوستس، على ارتفاع 147 مترًا فوق قاعدتها ويبلغ ارتفاعها فوق مستوى سطح البحر 195 مترًا ( الشكل 8.3 ). (تم تبني اسمها الأمريكي الأصلي، ماساتشوست، من قبل المستوطنين لتسمية مستعمرة الخليج والدولة بالقرب من موقعها). يصعد متنزه وزنه 75 كجم من القاعدة إلى القمة. ما هي طاقة الجاذبية الكامنة لنظام Hiker-Earth فيما يتعلق بصفر طاقة الجاذبية الكامنة عند ارتفاع القاعدة، عندما يكون المتجول (أ) عند قاعدة التل، (ب) في القمة، (ج) في مستوى سطح البحر، بعد ذلك؟

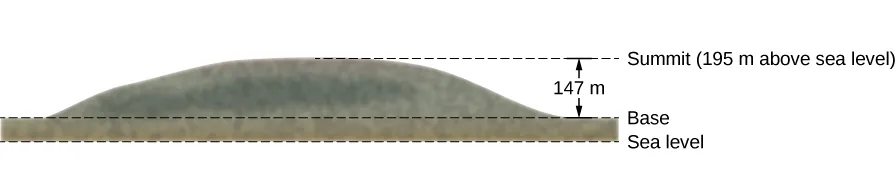
الشكل 8.3: رسم تخطيطي لملف جريت بلو هيل، ميلتون، ماساتشوستس. يشار إلى ارتفاعات المستويات الثلاثة.

استراتيجية الحل

أولًا، علينا اختيار أصل المحور y ثم تحديد قيمة الثابت الذي يجعل الطاقة الكامنة تساوي صفرًا عند ارتفاع القاعدة. بعد ذلك، يمكننا تحديد الطاقات الكامنة من المعادلة 8.5، بناءً على العلاقة بين ارتفاع الطاقة الكامنة الصفري والارتفاع الذي يقع عنده المتنزه.

الحل

(أ) دعنا نختار أصل المحور y عند ارتفاع القاعدة، حيث نريد أيضًا أن يكون صفر من الطاقة الكامنة. هذا الاختيار يجعل الثابت يساوي صفرًا ويجعل:

U (base) = U (0) = 0 .

(ب) في القمة، y=147 m، ولذا:

U (summit) = U (147 m) = m g h = (75 \times 9.8 N) (147 m) = 108 kJ .

(ج) على مستوى سطح البحر، y=(147-195)m= -48 m، لذا:

U (sea-level) = (75 \times 9.8 N) (−48 m) = −35.3 kJ .

الدلالة

إلى جانب توضيح استخدام المعادلة 8.4 والمعادلة 8.5، فإن قيم طاقة الجاذبية الكامنة التي وجدناها معقولة. تكون طاقة الجاذبية الكامنة أعلى عند القمة منها عند القاعدة، وأقل عند مستوى سطح البحر عنها في القاعدة. تعمل الجاذبية معك في طريقك للأعلى أيضًا! إنها تقوم بشغل سلبي وليس بنفس القدر (من حيث المقدار)، كما تفعل عضلاتك. لكنها بالتأكيد تبذل شغل. وبالمثل، تبذل عضلاتك الشغل في طريقك إلى أسفل، كشغل سلبي. تعتمد القيم العددية للطاقات الكامنة على اختيار صفر للطاقة الكامنة، لكن الفروق المادية ذات المعنى للطاقة الكامنة لا تفعل ذلك. لاحظ أنه نظرًا لأن المعادلة 8.2 هي الفرق، فإن القيم العددية لا تعتمد على أصل الإحداثيات.

تحقق من فهمك 8.2

ما هي قيم طاقة الجاذبية الكامنة للمتنزه عند القاعدة، والقمة، ومستوى سطح البحر، فيما يتعلق بصفر مستوى سطح البحر من الطاقة الكامنة؟

الطاقة الكامنة المرنة

في الشغل، رأينا أن الشغل المنجز بواسطة زنبرك مرن تمامًا، في بُعد واحد، يعتمد فقط على ثابت الزنبرك ومربعات الإزاحة من الموضع غير الممدود، كما هو موضح في المعادلة 7.5. يتضمن هذا العمل فقط خصائص تفاعل قانون هوك وليس خصائص الزنبرك الحقيقي وأي أشياء مرتبطة به. لذلك، يمكننا تحديد فرق الطاقة الكامنة المرنة لقوة زنبركية على أنها سالب الشغل الذي تقوم به قوة الزنبرك في هذه المعادلة، قبل أن نفكر في الأنظمة التي تجسد هذا النوع من القوة. وبالتالي لدينا:

Δ U = − W_{A B} = \frac{1}{2} k (x_{B}^{2} - x_{A}^{2}),

8.6

حيث ينتقل الكائن من النقطة أ إلى النقطة ب. دالة الطاقة الكامنة المقابلة لهذا الاختلاف هي:

U (x) = \frac{1}{2} k x^{2} + const .

8.7

إذا كانت قوة الزنبرك هي القوة الوحيدة المؤثرة، فمن الأسهل أخذ صفر من الطاقة الكامنة عند x-0، عندما يكون الزنبرك بطول غير ممتد. ثم، الثابت في المعادلة 8.7 هو صفر. (قد تكون الخيارات الأخرى أكثر ملاءمة إذا كانت هناك قوى أخرى تعمل).

مثال 8.3: طاقة الزنبرك الكامنة

يحتوي النظام على زنبرك مرن تمامًا، بطول غير ممتد 20 سم وثابت زنبرك 4 نيوتن / سم. (أ) ما مقدار الطاقة الكامنة المرنة التي يساهم بها الزنبرك عندما يكون طوله 23 سم؟ (ب) ما مقدار الطاقة الكامنة التي يساهم بها إذا زاد طوله إلى 26 سم؟

استراتيجية الحل

عندما يكون الزنبرك بطول غير ممتد، فإنه لا يساهم بأي شيء في الطاقة الكامنة للنظام، لذلك يمكننا استخدام المعادلة 8.7 مع الثابت الذي يساوي الصفر. قيمة x هي الطول مطروحًا منه الطول غير الممدود. عندما يتمدد الزنبرك، يجب استخدام إزاحة الزنبرك أو الفرق بين طوله المريح والطول الممدود من أجل قيمة x-value في حساب الطاقة الكامنة للزنبرك.

الحل

(أ) إزاحة الزنبرك = 23سم – 20 سم = 3 سم

لذلك فإن الطاقة الكامنة هي:

U = \frac{1}{2} k x^{2} = \frac{1}{2} (4 N/cm) {(3 cm)}^{2} = 0.18 J

(ب) عندما تكون إزاحة الزنبرك = 26 سم – 20 سم = 6 سم

فإن الطاقة الكامنة تكون:

U = \frac{1}{2} k x^{2} = \frac{1}{2} (4 N/cm) {(6 cm)}^{2} = 0.72 J

وهي زيادة بمقدار -0.54 جول عن القيمة الواردة في الجزء (أ).

الدلالة

يتضمن حساب الطاقة الكامنة المرنة والفرق بين الطاقة الكامنة من المعادلة 8.7 حل الطاقات الكامنة بناءً على أطوال الزنبرك المعطاة. حيث U تعتمد على x²، الطاقة الكامنة للضغط (سالب x) هي نفسها بالنسبة للتمدد المساوي للقيمة.

تحقق من فهمك 8.3

عندما يتغير طول الزنبرك في مثال 8.3 من قيمة أولية قدرها 22.0 سم إلى قيمة نهائية، تتغير الطاقة الكامنة المرنة التي يساهم بها – 0.08 جول. أوجد الطول النهائي.

طاقة الوضع الجاذبية والمرنة

النظام البسيط الذي يجسد كلاً من أنواع الجاذبية والمرونة من الطاقة الكامنة هو نظام زنبركي عمودي أحادي البعد. يتكون هذا من جسيم ضخم (أو كتلة)، معلق من أحد طرفي زنبرك عديم الكتلة ومرن تمامًا، والطرف الآخر منه ثابت، كما هو موضح في الشكل 8.4.

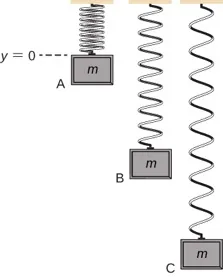
شكل 8.4: نظام زنبركي عمودي، مع اتجاه المحور y الموجب لأعلى. تكون الكتلة مبدئيًا بطول زنبرك غير ممتد، النقطة A. ثم يتم تحريرها، وتتوسع بعد النقطة B إلى النقطة C، حيث تتوقف.

أولاً، دعنا نفكر في الطاقة الكامنة للنظام. نحتاج إلى تحديد الثابت في دالة الطاقة الكامنة في المعادلة 8.5. غالبًا ما تكون الأرض خيارًا مناسبًا عندما تكون طاقة وضع الجاذبية صفرًا؛ ومع ذلك، في هذه الحالة، أعلى نقطة أو عندما تكون y=0 هو موقع مناسب لطاقة كامنة منعدمة الجاذبية. لاحظ أن هذا الاختيار تعسفي، ويمكن حل المسألة بشكل صحيح حتى إذا تم اختيار خيار آخر.

يجب علينا أيضًا تحديد الطاقة الكامنة المرنة للنظام والثابت المقابل، كما هو مفصل في المعادلة 8.7. هذا هو المكان الذي يكون فيه الزنبرك غير ممتد، أو عند موضع y=0.

إذا اعتبرنا أن الطاقة الكلية للنظام محفوظة، فإن الطاقة عند النقطة A تساوي الطاقة عند النقطة C. يتم وضع الكتلة على الزنبرك مباشرةً، وبالتالي فإن طاقته الحركية الأولية تساوي صفرًا. من خلال إعداد المسألة التي تمت مناقشتها سابقًا، كل من طاقة وضع الجاذبية وطاقة الوضع المرنة تساوي الصفر. لذلك، الطاقة الأولية للنظام هي صفر. عندما تصل الكتلة إلى النقطة C، فإن طاقتها الحركية تساوي صفرًا. ومع ذلك، لديها الآن كلاً من طاقة الجاذبية الكامنة وطاقة الوضع المرنة. لذلك، يمكننا إيجاد المسافة y التي تقطعها الكتلة قبل أن تتوقف:

\begin{matrix} K_{A} & + & U_{A} = K_{C} + U_{C} \\ 0 & = & 0 + m g y_{C} + {\frac{1}{2} k (y_{C})}^{2} \\ y_{C} & = & \frac{- 2 m g}{k} \end{matrix}

الشكل 8.5: يحوّل المتزلق طاقة وضع الجاذبية في بداية القفزة إلى طاقة وضع مرنة في أسفل القفزة.

مثال 8.4: الطاقة الكامنة لنظام الزنبرك العمودي

كتلة تزن 2.1 كيلوجرام، معلَّقة من زنبرك مع ثابت زنبركي يساوي 6.0 نيوتن/متر، كما هو موضح في الشكل 8.4. (أ) ما أقصى تمدد للزنبرك، كما يظهر عند النقطة C؟ (ب) ما هي الطاقة الكامنة الكلية عند النقطة B في منتصف المسافة بين A و C؟ (ج) ما سرعة الكتلة عند النقطة B؟

استراتيجية الحل

في الجزء (أ) نحسب المسافة y_C كما تمت مناقشته في النص السابق. ثم في الجزء (ب)، نستخدم نصف قيمة y لحساب الطاقة الكامنة عند النقطة B باستخدام المعادلتين 8.4 والمعادلة 8.6. يجب أن تكون هذه الطاقة مساوية للطاقة الحركية، المعادلة 7.6، عند النقطة B لأن الطاقة الأولية للنظام هي صفر. بحساب الطاقة الحركية عند النقطة B، يمكننا الآن حساب سرعة الكتلة عند النقطة B.

الحل

(أ) نظرًا لأن الطاقة الإجمالية للنظام تساوي صفرًا عند النقطة A كما تمت مناقشته سابقًا، يتم حساب أقصى تمدد للزنبرك ليكون:

\begin{matrix} y_{C} & = & \frac{- 2 m g}{k} \\ y_{C} & = & \frac{- 2 (1.2 N)}{(6.0 N/m)} = -0.40 m \end{matrix}

(ب) موضع y_B هو نصف الموضع y_C وبالتالي، فإن إجمالي الطاقة الكامنة عند النقطة B سيكون:

\begin{matrix} U_{B} & = & m g y_{B} + {\frac{1}{2} k (y_{B})}^{2} \\ U_{B} & = & (1.2 N) (-0.20 m) + {\frac{1}{2} (6 N/m) (- 0.20 m)}^{2} \\ U_{B} & = & - 0.12 J \end{matrix}

(ج) كتلة الجسم هي الوزن مقسومًا على الجاذبية.

m = \frac{F_{w}}{g} = \frac{1.2 N}{9.8 {m/s}^{2}} = 0.12 kg

وبالتالي، فإن الطاقة الحركية عند النقطة B تساوي 0.12 جول لأن الطاقة الإجمالية تساوي صفرًا. لذلك، فإن سرعة الكتلة عند النقطة B تساوي:

\begin{matrix} K = & \frac{1}{2} m v^{2} \\ v = & \sqrt{\frac{2 K}{m}} = \sqrt{\frac{2 (0.12 J)}{(0.12 kg)}} = 1.4 m/s \end{matrix}

الدلالة

على الرغم من أن الطاقة الكامنة بسبب الجاذبية مرتبطة بموقع الصفر المختار، فإن حل هذه المسألة ستكون هي نفسها إذا تم اختيار نقاط الطاقة الصفرية في مواقع مختلفة.

تحقق من فهمك 8.4

افترض أن الكتلة في المعادلة 8.6 تضاعفت مع الحفاظ على جميع الشروط الأخرى كما هي. هل سيزداد الحد الأقصى لتمدد الزنبرك أم ينقص أم يظل كما هو؟ هل ستكون السرعة عند النقطة B أكبر أم أصغر أم هي نفسها مقارنةً بالكتلة الأصلية؟

يوضح الجدول 8.1 نموذج مخطط لمجموعة متنوعة من الطاقات لإعطائك فكرة عن قيم الطاقة النموذجية المرتبطة بأحداث معينة. يتم حساب بعضها باستخدام الطاقة الحركية، في حين يتم حساب البعض الآخر باستخدام الكميات الموجودة في شكل من أشكال الطاقة الكامنة التي ربما لم تتم مناقشتها في هذه المرحلة.

الكائن / الظاهرة	الطاقة بالجول
الانفجار العظيم	10 ⁶⁸
الاستخدام السنوي للطاقة في العالم	4.0 × 10 ²⁰
قنبلة اندماجية كبيرة (9 ميغا طن)	3.8 × 10 ¹⁶
قنبلة انشطارية بحجم هيروشيما (10 كيلوطن)	4.2 × 10 ¹³
1 برميل نفط خام	5.9 × 10⁹
1 طن متري من مادة تي إن تي	4.2 × 10 ⁹
1 جالون بنزين	1.2 × 10 ⁸
تناول الطعام اليومي للبالغين (موصى به)	1.2 × 10 ⁷
سيارة وزن 1000 كجم بسرعة 90 كم / ساعة	3.1 × 10 ⁵
كرة التنس بسرعة 100 كم / ساعة	22
البعوض (10⁻² جرام عند 0.5 م / ث)	1.3 × 10 ⁻⁶
إلكترون واحد في شعاع أنبوب التلفزيون	4.0 × 10 ⁻¹⁵
طاقة لكسر خيط واحد من الحمض النووي	10 ⁻¹⁹
1 كجم هيدروجين (اندماج إلى هيليوم)	6.4 × 10 ¹⁴
1 كجم من اليورانيوم (انشطار نووي)	8.0 × 10 ¹³

جدول 8.1: طاقة الأجسام والظواهر المختلفة

المراجع

موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2023.
كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.