السرعة اللحظية والسرعة المتوسطة

الأهداف: بنهاية هذا القسم حول موضوع السرعة والسرعة اللحظية، سيكون القارئ قادرًا على:

شرح الفرق بين السرعة المتوسطة والسرعة اللحظية.
وصف الفرق بين مقدار السرعة ومتجه السرعة.
حساب السرعة اللحظية مع الأخذ في الاعتبار المعادلة الرياضية للسرعة.
حساب السرعة بناءً على السرعة اللحظية.

المحتويات

لقد رأينا الآن كيفية حساب السرعة المتوسطة بين موضعين. ومع ذلك، نظرًا لأن الكائنات في العالم الحقيقي تتحرك بشكل مستمر عبر المكان والزمان، فإننا نرغب في معرفة سرعة أي جسم في أي نقطة مفردة. يمكننا إيجاد سرعة الجسم في أي مكان على مساره باستخدام بعض المبادئ الأساسية لحساب التفاضل والتكامل. يعطينا هذا القسم نظرة ثاقبة في فيزياء الحركة وسيكون مفيدًا في فصول لاحقة.

السرعة اللحظية

الكمية التي تخبرنا بمدى سرعة تحرك جسم ما في أي مكان على طول مساره هي السرعة اللحظية أو Instantaneous Velocity، والتي تسمى عادةً السرعة. إنها السرعة المتوسطة بين نقطتين على المسار في الحد الذي يقترب فيه الوقت (وبالتالي الإزاحة) بين النقطتين من الصفر. لتوضيح هذه الفكرة رياضيًا، نحتاج إلى التعبير عن الموضع x كدالة متصلة لـ t يُرمز إليها بـ x(t). التعبير عن السرعة المتوسطة بين نقطتين باستخدام هذا الرمز هو:

v – = [x(t₂) – x(t₁)] / (t₂ – t₁)

لإيجاد السرعة اللحظية في أي موضع، نجعل t₁ = t و t₂ = t + Δt. بعد إدخال هذه التعبيرات في معادلة السرعة المتوسطة وأخذ النهاية عندما تؤول Δt → 0، نجد التعبير عن السرعة اللحظية كما يلي:

v (t) = lim_{Δ t \to 0} \frac{x (t + Δ t) - x (t)}{Δ t} = \frac{d x (t)}{d t} .

معادلة حساب السرعة اللحظية

السرعة اللحظية لجسم ما هي نهاية متوسط السرعة مع اقتراب الوقت المنقضي من الصفر، أو هي المشتقة الأولى لدالة الإزاحة x بالنسبة إلى الزمن t:

v (t) = \frac{d}{d t} x (t) .

(3.4)

مثل السرعة المتوسطة، السرعة اللحظية هي متجه بأبعاد المسافة مقسومة على الزمن. السرعة اللحظية عند نقطة زمنية محددة t₀ هي معدل تغير دالة الموضع، وهو ميل دالة الموضع x(t) عند t₀. يوضح الشكل 3.6 كيف يقترب متوسط السرعة v = Δx/Δt بين مرتين من السرعة اللحظية عند t₀.

يتم عرض السرعة اللحظية في الوقت t₀، والتي تصادف أن تكون عند الحد الأقصى لدالة الموضع. ميل الرسم البياني للموضع يساوي صفرًا عند هذه النقطة، وبالتالي فإن السرعة اللحظية تساوي صفرًا. في أوقات أخرى، t₁ و t₂ وما إلى ذلك، لا تكون السرعة اللحظية صفرًا لأن ميل الرسم البياني للموضع سيكون موجبًا أو سالبًا. إذا كان لدالة الموضع حد أدنى، فسيكون ميل الرسم البياني للموضع صفرًا أيضًا، مما يعطي سرعة لحظية تساوي صفرًا أيضًا. وبالتالي، فإن أصفار دالة السرعة تعطي الحد الأدنى والأقصى لدالة الموضع.

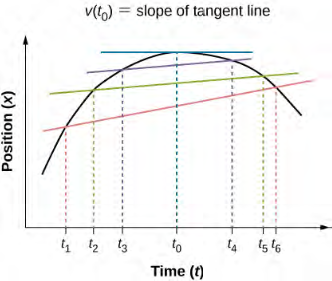
السرعة اللحظية والسرعة المتوسطة - الشكل 3.6: في الرسم البياني للموضع مقابل الوقت — السرعة اللحظية والسرعة المتوسطة – الشكل 3.6: في الرسم البياني للموضع مقابل الوقت

الشكل 3.6: في الرسم البياني للموضع مقابل الوقت، تكون السرعة اللحظية هي ميل خط المماس عند نقطة معينة. يتم عرض متوسط السرعات v = Δx/Δt = (x_f – x_i)/(t_f – t_i) بين الأوقات Δt = t₆ – t₁ ، Δt = t₅ – t₂ ، و t = t₄ – t₃. عندما Δt → 0، تقترب السرعة المتوسطة من السرعة اللحظية عند t = t₀.

مثال3.2: إيجاد السرعة من رسم بياني للموضع مقابل الوقت

بالنظر إلى الرسم البياني للموضع مقابل الوقت بالشكل 3.7، أوجد الرسم البياني للسرعة مقابل الوقت.

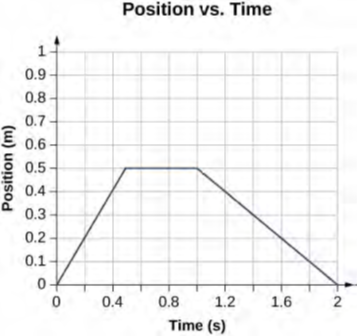
السرعة اللحظية والسرعة المتوسطة - الشكل 3.7: يبدأ الكائن في الاتجاه الموجب، ويتوقف لفترة قصيرة، ثم ينعكس الاتجاه، متجهًا نحو الأصل — السرعة اللحظية والسرعة المتوسطة – الشكل 3.7: يبدأ الكائن في الاتجاه الموجب، ويتوقف لفترة قصيرة، ثم ينعكس الاتجاه، متجهًا نحو الأصل

الشكل 3.7: يبدأ الكائن في الاتجاه الموجب، ويتوقف لفترة قصيرة، ثم ينعكس الاتجاه، متجهًا نحو الأصل. لاحظ أن الجسم يتوقف على الفور، الأمر الذي يتطلب قوة غير محدودة. وبالتالي، فإن الرسم البياني هو تقريب للحركة في العالم الحقيقي. (تمت مناقشة مفهوم القوة في قوانين نيوتن للحركة).

إستراتيجية الحل

يحتوي الرسم البياني على ثلاثة خطوط مستقيمة خلال فترات زمنية ثلاث. نحسب السرعة خلال كل فترة زمنية عن طريق أخذ ميل الخط المستقيم باستخدام الشبكة.

الحل

الفترة الزمنية الأولى: من صفر إلى 0.5 ثانية

v = Δx / Δt = (0.5 m − 0.0 m) / (0.5 s − 0.0 s) = 1.0 m/s

ثم الفترة الزمنية الثانية: من 0.5 إلى 1.0 ثانية:

v = Δx /Δt = (0.5 m − 0.5 m) / (1.0 s − 0.5 s) = 0.0 m/s

ثم الفترة الزمنية الثالثة: من 1.0 إلى 2.0 ثانية:

v = Δx / Δt = (0.0 m − 0.5 m) / (2.0 s − 1.0 s) = − 0.5 m/s

يظهر الرسم البياني لقيم هذه السرعة مقابل الوقت في الشكل 3.8.

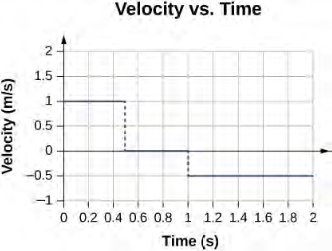
الشكل 3.8: السرعة موجبة للجزء الأول من الرحلة، وصفر عند توقف الجسم، وسالبة عندما يعكس الجسم اتجاهه

الدلالة

خلال الفترة الزمنية بين صفر ثانية و0.5 ثانية، يتحرك موضع الكائن بعيدًا عن الأصل ويكون لمنحنى الموضع مقابل الوقت ميلًا إيجابيًا. في أي نقطة على طول المنحنى خلال هذه الفترة الزمنية، يمكننا إيجاد السرعة اللحظية بأخذ ميلها، وهو +1 متر / ثانية، كما هو موضح في الشكل 3.8. في الفترة الزمنية اللاحقة، بين 0.5 ثانية و1.0 ثانية، لا يتغير الموضع ونلاحظ أن الميل يساوي صفرًا. من 1.0 ثانية إلى 2.0 ثانية، يتحرك الجسم للخلف باتجاه الأصل والميل هو 0.5 متر/ثانية. عكس الجسم اتجاهه وله سرعة سالبة.

السرعة ومتجه السرعة

في اللغة اليومية، يستخدم معظم الناس مصطلحي السرعة Speed ومتجه السرعة Velocity بالتبادل. ومع ذلك، في الفيزياء، ليس لها نفس المعنى وهي مفاهيم مختلفة. أحد الاختلافات الرئيسية هو أن السرعة ليس لها اتجاه؛ وهذا يعني أن السرعة كمية قياسية عددية وليست كمية متجهة.

يمكننا حساب متوسط السرعة Average Speed بإيجاد المسافة الإجمالية المقطوعة مقسومة على الوقت المنقضي:

Average speed = \overset{–}{s} = \frac{Total distance}{Elapsed time} .

(3.5)

متوسط السرعة أو Average speed ليس بالضرورة هو نفسه مقدار متجه السرعة المتوسطة Average velocity، والتي يمكن إيجادها بقسمة حجم الإزاحة الكلية على الوقت المنقضي. على سبيل المثال، إذا بدأت الرحلة وانتهت في نفس الموقع، فإن إجمالي الإزاحة يساوي صفرًا، وبالتالي يكون متجه السرعة المتوسطة صفرًا. ومع ذلك، فإن متوسط السرعة ليس صفرًا، لأن المسافة الإجمالية المقطوعة أكبر من الصفر. إذا قمنا برحلة برية طولها 300 كيلومتر وتحتاج إلى الوصول إلى وجهتنا في وقت معين، فسنكون مهتمين بمتوسط سرعتنا.

ومع ذلك، يمكننا حساب السرعة اللحظية القياسية من مقدار متجه السرعة اللحظية:

Instantaneous speed = | v (t) | .

(3.6)

إذا كان جسم ما يتحرك على طول المحور x عند سرعة +7.0 m/s وجسيم آخر يتحرك على نفس المحور عند سرعة -7.0 m/s، فإن متجهات سرعتهما مختلفة Velocity، لكن كلاهما لهما نفس السرعة Speed البالغة 7 متر/ثانية.

بعض السرعات النموذجية

بعض السرعات النموذجية موضحة في الجدول التالي:

السرعة	متر/ثانية	ميل/ساعة
الانجراف القاري	10^-7	2 * 10^-7
المشي السريع	1.7	3.9
الدراجة	4.4	10
العداء السريع	12.2	27
الحد الأقصى للسرعة في الريف	24.6	56
الرقم القياسي الرسمي لسرعة الأرض	341.1	763
سرعة الصوت عند مستوى سطح البحر	343	768
مكوك الفضاء عند العودة	7800	17500
سرعة الهروب من الأرض *	11200	25000
السرعة المدارية للأرض حول الشمس	29783	66623
سرعة الضوء في الفراغ	299,792,458	670,616,629

جدول بعض السرعات النموذجية

الجدول 3.1 سرعات الأجسام المختلفة * سرعة الهروب هي السرعة التي يجب أن يتم بها إطلاق الجسم بحيث يتغلب على جاذبية الأرض ولا يتم سحبه أو جذبه للخلف باتجاه الأرض.

حساب السرعة اللحظية

عند حساب السرعة اللحظية، نحتاج إلى تحديد الشكل الصريح لدالة الموضع x(t). في الوقت الحالي، دعنا نستخدم كثيرات الحدود x(t) = Atⁿ، لأنه يمكن تمييزها بسهولة باستخدام قاعدة الأسس في حساب التفاضل والتكامل:

\frac{d (A t^{n})}{d t} = A n t^{n - 1} .

(3.7)

يوضح المثال التالي استخدام المعادلة 3.7.

مثال 3.3: السرعة اللحظية مقابل السرعة المتوسطة

يُعطى موضع الجسيم بواسطة المعادلة التالية:

x (t) = (3.0 m/s) t + (0.5 {m/s}^{3}) t^{3}

أ. باستخدام المعادلة 3.4 والمعادلة 3.7، أوجد السرعة اللحظية عند t = 2.0 s.

ب. احسب السرعة المتوسطة للجسم بين الثانية 1.0 ث والثانية 3.0 ث.

إستراتيجية الحل

تعطي المعادلة (3.4) السرعة اللحظية للجسيم كمشتقة لدالة الموضع. بالنظر إلى شكل دالة الموضع المعطاة، نلاحظ أنها كثيرة الحدود في t. لذلك، يمكننا استخدام المعادلة (3.7)، قاعدة الأسس من التفاضل والتكامل، لإيجاد الحل. ثم نستخدم المعادلة (3.6) لحساب متوسط سرعة الجسيم.

الحل

أ.

v (t) = \frac{d x (t)}{d t} = (3.0 m/s) + (1.5 {m/s}^{3}) t^{2}

ثم بالتعويض عن t = 2.0 s في هذه المعادلة، نحصل على:

v (2.0 s) = (3.0 m/s) + (1.5 {m/s}^{3}) {(2.0 s)}^{2}

ب.

لتحديد متوسط سرعة الجسيم بين الثانية 1.0 والثانية 3.0، نحسب قيم x (1.0 s) و x (3.0s):

x (1.0 s) = [(3.0 m/s) (1.0 s) + (0.5 {m/s}^{3}) {(1.0 s)}^{3}] = 3.5 m

x (3.0 s) = [(3.0 m/s) (3.0 s) + (0.5 {m/s}^{3}) {(3.0 s)}^{3}] = 22.5 m

ثم السرعة المتوسطة تكون:

\overset{–}{v} = \frac{x (3.0 s) - x (1.0 s)}{t (3.0 s) - t (1.0 s)} = \frac{(22.5 - 3.5) m}{(3.0 - 1.0) s} = 9.5 m/s .

الدلالة

في النهاية التي تستخدم فيها الفترة الزمنية لحساب السرعة اللحظية v والتي تؤول إلى الصفر، فإن القيمة التي تم الحصول عليها لمتجه السرعة v تتقارب مع القيمة العددية للسرعة v.

مثال 3.4: السرعة اللحظية مقابل السرعة

ليكن لدينا حركة جسم يكون موضعه معطى بالمعادلة التالية:

x (t) = (3.0 m/s) t - (3 {m/s}^{2}) t^{2}

أ. ما هي السرعة اللحظية instantaneous velocity عند t = 0.25 s وعند t = 0.50 s وعند t = 1.0 s؟

ب. ما هو مقدار سرعة الجسيم speed في تلك الأوقات؟

إستراتيجية الحل

السرعة اللحظية هي مشتق من دالة الموضع (أو الموقع) والسرعة هي مقدار السرعة اللحظية أي القيمة العددية لها. نستخدم المعادلة 3.4 والمعادلة 3.7 لإيجاد السرعة اللحظية.

الحل

أ. السرعة اللحظية

v (t) = \frac{d x (t)}{d t} = (3.0 m/s - 6.0 {m/s}^{2} t) v (0.25 s) = 1.50 m/s,

v (0.5 s) = 0 m/s, v (1.0 s) = −3.0 m/s

ب. مقدار السرعة

Speed = | v (t) | = 1.50 m/s, 0.0 m/s, and 3.0 m/s

الدلالة

يعطينا متجه سرعة الجسيم معلومات عن الاتجاه، مما يشير إلى أن الجسيم يتحرك إلى اليسار (الغرب) أو اليمين (الشرق). تعطي السرعة مقدار السرعة. من خلال رسم الموضع ومتجه السرعة والسرعة كدالات زمنية، يمكننا فهم هذه المفاهيم بصريًا.

الشكل 3.9. في (a)، يوضح الرسم البياني أن الجسيم يتحرك في الاتجاه الموجب حتى الثانية t = 0.5 s، عندما ينعكس الاتجاه. يمكن أيضًا رؤية انعكاس الاتجاه في (b) عند الثانية 0.5 حيث تكون السرعة صفرًا ثم تصبح سالبة. عند 1.0 ثانية، عادت إلى الأصل حيث بدأت. سرعة الجسيم عند 1.0 ثانية في (b) سالبة، لأنها تتحرك في الاتجاه السالب. ولكن في (c)، تكون سرعته موجبة وتظل موجبة طوال فترة السفر. يمكننا أيضًا تفسير السرعة على أنها ميل الرسم البياني للموضع مقابل الوقت. منحنى x(t) يتناقص باتجاه الصفر، ويصبح صفرًا عند 0.5 ثانية ثم يتزايد سالبًا بعد ذلك.

يساعد هذا التحليل لمقارنة الرسوم البيانية للموضع ومتجه السرعة والسرعة في اكتشاف الأخطاء في الحسابات. يجب أن تكون الرسوم أو الأشكال البيانية متسقة مع بعضها البعض وتساعد في تفسير الحسابات.

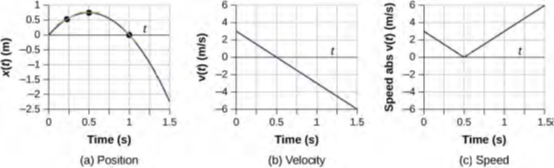
الشكل 3.9 (a) المركز: x(t) مقابل الوقت. (b) السرعة: v(t) مقابل الوقت أو الزمن. ميل الرسم البياني للموضع هو السرعة. تشير المقارنة التقريبية لمنحدرات خطوط الظل في (a) عند 0.25 ثانية و0.5 ثانية و1.0 ثانية مع قيم السرعة في الأوقات المقابلة إلى أنهما نفس القيم. (c) مقدار السرعة:|v(t)| مقابل الوقت. السرعة دائمًا رقم موجب.

تحقق من فهمك

موضع الكائن كدالة للوقت هو x (t) = −3t² m. (أ) ما سرعة الجسم بدلالة الزمن؟ (ب) هل السرعة موجبة دائمًا؟ (ج) ما متجه السرعة ومقدار السرعة عند الثانية t = 1.0 s؟

المصدر

موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.