الرياضيات و قدرات الحساب والمنطق

الرياضيات والتفكير المنطقي

يشتمل التفكير المنطقي المجرد على الكثير من الجوانب التفصيلية، كما أنه يتغير بتغير الأساس المنطقي الذي يتم البناء عليه، وبطبيعة الحال سوف يختلف المنطق الرياضي من شخص لآخر بحسب ما يعتقده كل شخص وما يتخذه أساسًا للبناء عليه. ففي مقررات الجبر في الرياضيات مثلا، يتم البناء المعرفي بشكل تراكمي من خلال مسلمات ونظريات تُستخدم بعد ذلك في حل المسائل المتنوعة وفقًا لها، باعتبارها من أسس المنطق الرياضي التي يتم الاستناد عليها للتوصل لتلك الحلول.

و المنطق الرياضي يختلف عن الصحة، بحيث أنه يمكن لإجابة ما أن تكون منطقية وبنفس الوقت لا تكون صحيحة، وذلك بحسب “الأساس المنطقي” الذي بُنيت عليه تلك الإجابة.

مثلا، لو افترضنا، مجازًا، أنه لدينا الأساس الذي يمثل المنطق الرياضي التالي:

• 1 + 1 = 5
• 2 + 2 = 10
• 3 + 3 = 15

فإنه بالاستناد إلى هذا الأساس يكون من المنطق الرياضي أن نستنتج أن:

6 + 6 = 30

ولكن الإجابة الصحيحة هي :

6 + 6 = 12

أي أن الاستنتاج الأول منطقي ولكنه غير صحيح حسابيًا.

أما الاستنتاج الثاني فهو صحيح حسابيًا ولكنه غير منطقي!!

الدوال الرياضية

يحتل موضوع الدوال الرياضية أو (بالإنجليزية: Functions) مكانة متميزة في الرياضيات لدرجة أنه يمكن ملاحظة وجوده في معظم فروع الرياضيات المختلفة. وبمرور الوقت يصبح التمكن من موضوع الدوال وفهمه بشكل جيد هو الطريق الأمثل لفهم الكثير من الموضوعات أو المسائل الأخرى في كل تلك الفروع.

وأبسط مثال لتوضيح ما هية الدالة وتوضيح طريقة استخدامها في الحياة اليومية هو فاتورة استهلاك الكهرباء أو الطاقة الشهرية.

فتلك الفاتورة عادة تحتوي على الرقم الذي يُستدل منه على عدد وحدات الاستهلاك باستخدام وحدة قياس القدرة الكهربائية الكيلو وات، ومنه نستطيع احتساب تكلفة هذا الاستهلاك من خلال معرفة سعر الكيلو وات الواحد كما يلي:

تكلفة الاستهلاك الشهري = سعر الوحدة * عدد وحدات الاستهلاك

وبفرض أن:

تكلفة الاستهلاك = ص

عدد وحدات الاستهلاك = س كيلو وات

سعر الوحدة = 7.5 قرش

فيكون لدينا الدالة التالية:

ص = د(س) = 7.5 س

فلو كان عدد وحدات الاستهلاك= 50، فإن تكلفة الاستهلاك سوف تكون مساوية لـ

تكلفة الاستهلاك = 7.5 * 50 = 375 قرش.

ولو كان عدد وحدات الاستهلاك= 100، فإن تكلفة الاستهلاك سوف تكون مساوية لـ

تكلفة الاستهلاك = 7.5 * 100 = 750 قرش.

وهكذا، سوف نستطيع دومًا معرفة قيمة تكلفة الاستهلاك الشهري إذا عرفنا عدد الوحدات المستهلكة.

وبمعنى آخر فإن عدد الوحدات المستهلكة بالكيلو وات سوف تدلنا على تكلفة قيمة الاستهلاك بالجنيه.

وبذلك يمكن أن نلخص موضوع الدوال بأنه وسيلة لمعرفة قيمة متغير معين (يُسمى متغير تابع) لن نستطيع معرفته إلاّ من خلال معرفة قيمة متغير آخر يدل عليه (يسمى متغير مستقل) من خلال علاقة محددة تُسمى دالة د(س).

لمزيد من التفصيل حول البيانات والمتغيرات يمكن قراءة موضوعات كل من:

قدرات التحليل

من أهم أهداف دراسة مقررات الرياضيات للطالب هي تنمية قدراته ومهاراته في المنطق الرياضي وتنمية قدرات التحليل المستندة على أسس منطقية متنوعة سواء كانت من منظور جبري مجرد أو من منظور هندسي حسي، وذلك من خلال مجموعة من المسلمات والنظريات التي يتم تدريسها طوال مدة الدراسة.

وتتنوع وتتدرج قدرات ومهارات التحليل التي تستهدفها دراسة مناهج الرياضيات في البلدان المختلفة حول العالم وذلك بحسب طبيعة ومحتوى المناهج المقررة فيها وخصائصها المختلفة.

ويمكن القول أن أفضل مناهج الرياضيات التي يمكنها أن تُنمي قدرات التحليل لدى الطالب بشكل مثالي هي تلك التي تعتني بتنمية قدرات التحليل بكافة مراحلها بشكل ضمني في محتوياتها، وهو ما تفتقده معظم مناهج الرياضيات حول العالم في الوقت الحالي!

القدرات التخيلية

من السمات المميزة لمقررات الهندسة الفراغية أنها تستند على قدرات الشق التخيلي في العقل بشكل أكبر من استنادها على قدرات الشق المنطقي فيه، بعكس مقررات أخرى مثل الجبر أو الحساب بشكل عام والتي تعتمد على التفكير المنطقي المجرد.

الشكل التالي يمثل اختبار بسيط لاستكشاف القدرة التخيلية لدى الطالب ومدى استعداده لفهم واستيعاب مقررات الهندسة الفراغية بشكل عام.

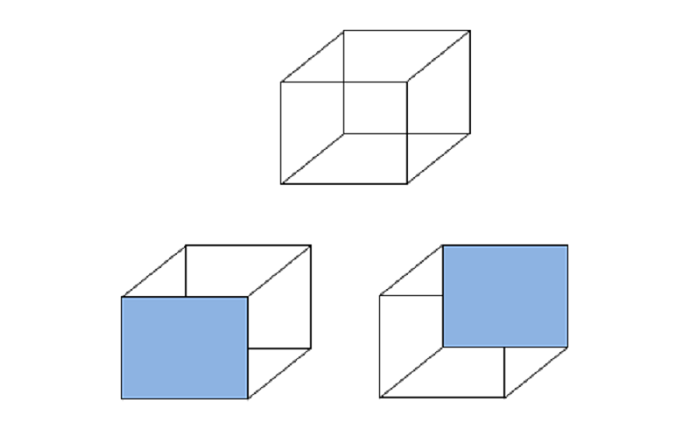
يمكن تطبيق الاختبار بسهولة من خلال البدء برسم كل المكعبات الثلاثة بدون التظليل باللون الأزرق والتي سوف تظهر جميعها متشابهة بدون اختلافات، وسؤال الطلاب عن تخيلهم لوضعية المكعبات كيف يمكن أن تكون، ومن ثم البدء بتظليل مكعبين منهم بطريقتين مختلفتين وإظهار الفرق بينهما كما هو موضح في الرسم أعلاه.

التخصصات الجامعية واختبارات القدرات

في جدول مفصل يُبين نتائج تقديرات اختبارات كل من القدرة اللغوية ومهارة الرياضيات ومجموعهما، بالإضافة لمتوسط مقياس نسبة الذكاء باستخدام اختبار الذكاء العالمي (IQ Test) لعدد من الخريجين الجامعيين في التخصصات الرئيسية المختلفة، أظهرت دراسة أعدها مركز خدمات الاختبارات التربوية الاختلافات المتنوعة لتلك القدرات وطريقة توزيعها وتكاملها لدى الخريجين الجامعيين في بعض التخصصات الأساسية أو الرئيسية.

وقياس نسبة الذكاء IQ عبارة عن درجة مشتقة من العديد من الاختبارات المعيارية التي صُممت لتقييم الذكاء، واختصار “IQ” يأتي من المصطلح الألماني Intelligenz-Quotient، والذي صاغه في الأصل عالم النفس وليام ستيرن.

وما يبدو واضحًا من الأرقام الواردة في الجدول أن هناك ضرورة للاهتمام بهذه الاختبارات التي تساعد في توجيه الطلاب نحو التخصصات المناسبة لهم ولقدراتهم المتنوعة بشكل تكاملي لنتائج كل اختبار بهدف الاستفادة منهم في المجتمع ولضمان نجاحهم، أو حتى تفوقهم، واستمرارهم في الدراسة الجامعية بالشكل الصحيح والمساعدة في الحد من عمليات السحب والتبديل أو التنقل بين التخصصات المختلفة بحثًا عن ما يناسبهم في الجامعات وما ينتج عنه من هدر للوقت والجهد والمصروفات الجامعية.

فوائد اختبارات القدرات

وفي الوقت الذي سيحتاج فيه الطالب إلى جهد مضاعف في حال الالتحاق بتخصصات تحتاج قدرات معينة أكبر مما يتوفر لديه، إلاّ أنه أيضًا سيبذل مجهود أقل مما ينبغي، أو حتى لا يبذل أي مجهود، في حال الالتحاق بتخصصات تحتاج أقل بكثير من قدراته، ولكن النتيجة في الحالتين ستكون سلبية لأنه ليس في مكانه المناسب وبالتالي لن يستفيد منه المجتمع كما ينبغي، ففي الحالة الأولى نجح بشق الأنفس وبطريقة قد أدت به لأن يكره التخصص ومن ثم يبتعد عنه بعد التخرج أو حتى يعمل به بشكل روتيني كأداء واجب، وفي الحالة الثانية نجح بسهولة وبدون مجهود وتخرج دون أن يشعر بانجذاب حقيقي للتخصص الأمر الذي يؤدي أيضًا للابتعاد عنه بعد التخرج أو تأديته بدون إضافة جديد أو أي إبداع.

لذا فإنه يكون من الحكمة محاولة الاستفادة من الاختبارات التربوية المتنوعة كأحد أدوات البحث العلمي الهادفة لاستكشاف قدرات الطلاب وتقديم ما يمكن أن يكون وسيلة إرشادية لهم لمعرفة التخصصات التي قد تكون أقرب لنمط تفكيرهم وقدراتهم المختلفة والتي تناسبهم لبدء مسيرتهم التعليمية الجامعية بالشكل الأمثل والابتعاد عن هدر الوقت والجهد وحتى المصروفات في تخصصات قد لا يستمرون فيها كلما أمكن ذلك.

ألغاز الرياضيات

فيما يلي بعض ألغاز الرياضيات التي تُعتبر من ألغاز الرياضيات المسلية يتم استثمارها بهدف قياس وتنمية مهارات التحليل والحساب والمنطق لدى الطلاب والباحثين من مختلف المجالات:

اللغز الأول

قبل بضعة سنوات احتفلنا بمناسبة نجاحنا في الثانوية العامة وكان ذلك في شهر يوليو ولكنني لا أذكر التاريخ بالتحديد. وعندما سألت زملائي عن تاريخ ذلك اليوم كانت إجاباتهم كالتالي:

الأول: أذكر أنه كان يوم فردي

الثاني: لم يكن مربعًا (أي لم يكن 1 – 4 – 9 – 16 – 25)

الثالث: كان مكعبًا (أي 1 – 8 – 27)

الرابع: كان بعد يوم 13 من الشهر (أي 14 – 15 – 16 -…)

الخامس: كان قبل يوم 17 من الشهر (أي 16 – 15 – 14 -…)

وقد قمت بعدها باسترجاع شريط تسجيل الحفل وتبين لي بأن 4 من أصدقائي كانت إجاباتهم خاطئة وواحد فقط كانت إجابته صحيحة.

فماذا كان تاريخ الحفل؟

اللغز الثاني

إذا كان اثنان من عمال الدهان يستغرقا 8 أيام لدهان شقة كاملة، أحدهما نشيط والثاني كسول.

وإذا كان العامل النشيط يستغرق 12 يوم لدهان نفس الشقة وحده بدون مساعدة العامل الكسول.

فكم يومًا يلزم للعامل الكسول حتى يدهن الشقة وحده بدون مساعدة العامل النشيط؟

ملاحظة: يجب كتابة الحل مع توضيح الطريقة

اللغز الثالث

في أحد الجامعات يقوم رئيس الجامعة بإجراءات مراسم افتتاح العام الدراسي بشكل عجيب..

يوجد في الجامعة عدد من الخزانات مقداره (1000) جرى ترقيمها من 1 لـ 1000 ويوجد نفس العدد من الطلاب الجدد (1000) أيضًا، حيث يطلب من الطالب الأول أن يقوم بالمرور على كل الخزانات ويفتحها، ويطلب من الطالب الثاني أن يقوم بالمرور على كل الخزانات التي هي من مضاعفات العدد (2) وإغلاقها، ثم يطلب من الطالب الثالث أن يقوم بالمرور على الخزانات التي هي من مضاعفات العدد (3) وإذا كانت مغلقة يفتحها وإذا كانت مفتوحة يغلقها، وبالمثل يطلب من الطالب الرابع أن يقوم بالمرور على الخزانات التي هي من مضاعفات العدد (4) وإذا وجدها مغلقة يفتحها وإذا وجدها مفتوحة يغلقها، وهكذا حتى الطالب رقم (1000).

السؤال هو: بعد إتمام كل العملية وقيام جميع الطلاب بمهمتهم بالترتيب والطريقة الموضحة أعلاه، كم عدد الخزانات التي ستكون مفتوحة؟

توضيح:

الطالب الأول: سيقوم بفتح جميع الخزانات

الطالب الثاني: سيقوم بإغلاق الخزانات رقم 2 – 4 – 6 – 8 – … الخ

الطالب الثالث سيقوم بفتح أو إغلاق الخزانات رقم: 3 – 6 – 9 – 10 … الخ

الطالب الرابع سيقوم بفتح أو إغلاق الخزانات رقم: 4 – 8 – 12 – 16 … إلخ

وهكذا.

اللغز الرابع

لدينا 50 قطعة نقود من نفس النوع موضوعة على طاولة، 25 منهم موضوعة على وجه الصورة و 25 على وجه الكتابة موزعة بشكل عشوائي، افترض انك تجلس أمام الطاولة معصوب العينين، ويمكنك أن تعرف أين قطع النقود وتمسكها وتقلبها ولكنك لا تستطيع أن تميز أذا كانت صورة أو كتابة.

السؤال هو: كيف يمكنك أن تقسم قطع النقود الخمسين إلى مجموعتين من القطع كل مجموعة تتكون من  25 قطعة، بحيث يكون في كل مجموعة نفس العدد من الصور والكتابة.

اللغز الخامس

لدينا ثلاث حنفيات مياه مختلفة:

1. الحنفية الأصغر تستطيع أن تملأ خزان مياه خلال 20 دقيقة
2. والحنفية المتوسطة تملأ نفس الخزان خلال 12 دقيقة
3. والحنفية الأكبر تملأ نفس الخزان خلال 5 دقائق

السؤال هو: كم دقيقة يلزم لتعبئة الخزان باستخدام الثلاث حنفيات معًا؟

اللغز السادس

في أحد الأسواق يوجد امرأتان تبيعان البرتقال، السيدة A والسيدة B.

وكانت السيدة A تبيع كل برتقالتين بنصف دولار.

والسيدة B تبيع كل ثلاث برتقالات بنصف دولار.

وفي لحظة ما، وعندما تبقى لدى كل من السيدتين نفس العدد من البرتقال، اضطرت السيدة B لمغادرة السوق لأمر طارئ وتركت ما تبقى من برتقال للسيدة A لكي تبيعه لها.

ولكي تسهل على نفسها عملية البيع، قامت السيدة A بوضع كل البرتقال في نفس السلة وبدأت تبيع كل 5 برتقالات بسعر دولار.

وفي نهاية اليوم عادت السيدة B وكان كل البرتقال قد تم بيعه، وعندما بدأتا بتقاسم المبلغ تبين أن هناك نقص مقداره ثلاثة دولارات ونصف.

السؤال هو:

بفرض أنهما تقاسمتا المبلغ المباع به البرتقال المشترك مناصفة، فكم هو المبلغ الذي تكون خسرته السيدة A في هذه العملية؟

اللغز السابع

يمتلك سالم مزرعة أبقار، وفي أحد الأيام قرر أن يحسب كم يومًا سيكفيه العشب المتوفر في المزرعة لإطعام الأبقار، ووجد أنه:

لو قام ببيع 75 بقرة من الأبقار التي يمتلكها الآن فإنه يستطيع أن يُطعم بقية الأبقار عشرون يومًا إضافيًا.

أما لو قام بشراء 100 بقرة وأضافها للأبقار الموجودة لديه الآن فإن العشب سينفذ قبل الموعد ب 15 يوم.

السؤال هو: كم بقرة يمتلك سالم في المزرعة؟