الحركة مع تسارع ثابت أو تسارع منتظم

الحركة مع تسارع ثابت أو تسارع منتظم

الأهداف: بنهاية هذا القسم حول موضوع الحركة مع تسارع ثابت سيكون القارئ قادرًا على:

• تحديد معادلات الحركة التي سيتم استخدامها لحل المجهول.
• استخدم معادلات الحركة المناسبة لحل مسائل المطاردة ثنائية الجسم.

قد تعتقد أنه كلما زادت تسارع، على سبيل المثال، تحرك السيارة بعيدًا عن علامة التوقف، زادت إزاحة السيارة في وقت معين. لكننا لم نطور معادلة محددة تتعلق بالتسارع والإزاحة. في هذا القسم، ننظر إلى بعض المعادلات الملائمة للعلاقات الحركية، بدءًا من تعريفات الإزاحة والسرعة والتسارع. نتحرى أولاً عن جسم واحد متحرك يسمى حركة الجسم الواحد. ثم نقوم بفحص حركة شيئين، تسمى مسائل المطاردة على الجسمين.

الرموز المستخدمة

أولاً، دعونا نجعل بعض التبسيط في التدوين. إن أخذ الوقت الأولي ليكون صفراً، كما لو كان الوقت يقاس بساعة توقيت، هو تبسيط كبير. بما أن الوقت المنقضي هو Δt = t_f – t₀، فإن أخذ t₀ = 0 يعني أن Δt = t_f، وهو الوقت الأخير على ساعة الإيقاف. عندما يتم أخذ الوقت الأولي ليكون صفرًا، فإننا نستخدم الرمز 0 للإشارة إلى القيم الأولية للموضع والسرعة.

أي أن x₀ هو الموضع الأولي و v₀ السرعة الابتدائية. نحن لا نضع أي رموز على القيم النهائية. أي أن t هي الوقت الأخير، و x هي الموضع الأخير، و v هي السرعة النهائية. وهذا يعطي تعبيرًا أبسط عن الوقت المنقضي، Δt = t. كما أنه يبسط التعبير عن الإزاحة x، والتي أصبحت الآن Δx = x – x₀. كما أنه يبسط التعبير عن التغيير في السرعة، والذي أصبح الآن Δv = v – v₀. للتلخيص، باستخدام الترميز المبسط، مع الوقت الأولي الذي يستغرقه ليكون صفرًا، يكون:

Δt = t

Δx = x − x₀

Δv = v − v₀

حيث يشير الرمز 0 إلى قيمة أولية ويشير غياب الرمز إلى القيمة النهائية في أي حركة قيد النظر.

متوسط التسارع والتسارع اللحظي

نفترض الآن أن التسارع ثابت. يسمح لنا هذا الافتراض بتجنب استخدام حساب التفاضل والتكامل لإيجاد التسارع اللحظي. نظرًا لأن التسارع ثابت، فإن متوسط التسارع والتسارع اللحظي متساويان، أي أن:

وبالتالي، يمكننا استخدام الرمز a للتسارع في جميع الأوقات. إن افتراض أن التسارع ثابت لا يحد بشكل خطير من المواقف التي يمكننا دراستها ولا يقلل من دقة علاجنا. لسبب واحد، التسارع ثابت في عدد كبير من المواقف. علاوة على ذلك، في العديد من المواقف الأخرى، يمكننا وصف الحركة بدقة من خلال افتراض تسارع ثابت يساوي متوسط تسارع تلك الحركة. أخيرًا، بالنسبة للحركة التي يتغير فيها التسارع بشكل كبير، مثل تسارع السيارة إلى السرعة القصوى ثم الكبح حتى التوقف، يمكن اعتبار الحركة في أجزاء منفصلة، لكل منها تسارعها الثابت.

إيجاد الإزاحة والموضع من السرعة

للحصول على المعادلتين الأوليين، نبدأ بتعريف السرعة المتوسطة v:

v = Δx / Δt

بالتعويض باستخدام الترميز المبسط لـ Δx وt ينتج:

v = (x − x₀) / t

وبحل هذه المعادلة للمجهول x:

(3.10)

حيث أن متوسط السرعة تساوي:

(3.11)

تعكس المعادلة v = (v₀ + v)/2 حقيقة أنه عندما يكون التسارع ثابتًا، فإن v هي مجرد متوسط بسيط للسرعتين الابتدائية والنهائية. يوضح الشكل 3.18 هذا المفهوم بيانيًا. في الجزء (a) من الشكل، يكون التسارع ثابتًا أو منتظمًا، مع زيادة السرعة بمعدل ثابت. متوسط السرعة خلال فترة 1 ساعة من 40 كم/ساعة إلى 80 كم/ساعة 60 كم/ساعة:

في الجزء (b)، التسارع ليس ثابتًا. خلال فترة 1 ساعة، تكون السرعة أقرب إلى 80 كم/ساعة من 40 كم/ساعة. وبالتالي، فإن متوسط السرعة أكبر من الجزء (a).

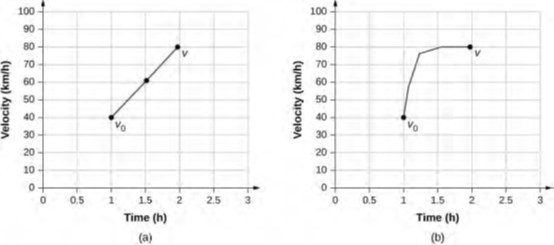
الشكل 3.18: (a) الرسم البياني للسرعة مقابل الوقت مع تسارع ثابت يوضح السرعات الأولية والنهائية v₀ و v. متوسط السرعة هو (v₀ + v)/2 = 60 km/h. (b) الرسم البياني للسرعة مقابل الوقت مع تسارع يتغير بمرور الوقت. لم يتم تحديد السرعة المتوسطة بمقدار v0 + v)/2)، ولكنها أكبر من 60 كم / ساعة.

إيجاد السرعة النهائية من التسارع الثابت والزمن

يمكننا اشتقاق معادلة مفيدة أخرى من خلال معالجة تعريف التسارع:

a = Δv /Δt

بالتعويض عن التعريف المبسط لـ Δv وt نحصل على:

a = (v − v₀) / t (constant a)

وبحل المعادلة بالنسبة لـ v ينتج معادلة حساب السرعة النهائية:

v = v₀ + at

(3.12)

مثال 3.7: حساب السرعة النهائية

تهبط طائرة بسرعة ابتدائية 70.0 متر / ث ثم تتباطأ عند 1.50 م / ث² لمدة 40.0 ثانية. ما هي سرعته النهائية؟

إستراتيجية الحل

أولاً، نحدد العناصر المعلومة من المعطيات:

v₀ = 70 m / s

a = −1.50 m / s²

t = 40 s

ثانيًا، نحدد المجهول؛ في هذه الحالة، تكون السرعة هي النهائية v_f.

أخيرًا، نحدد المعادلة التي يجب استخدامها. للقيام بذلك، نكتشف معادلة الحركة التي تعطي المجهول بدلالة المعطيات المعروفة. نحسب السرعة النهائية باستخدام المعادلة:

 v = v₀ + at

الحل

بالتعويض عن القيم المعروفة وحل المعادلة ينتج أن:

v = v₀ + at = 70.0 m/s + (−1.50 m/s2) * (40.0 s) = 10.0 m/s

الشكل 3.19 هو رسم بياني يوضح متجهي التسارع والسرعة:

في الشكل 3.19: تهبط الطائرة بسرعة ابتدائية 70.0 م / ث وتتباطأ إلى سرعة نهائية 10.0 م / ث قبل التوجه إلى المحطة. لاحظ أن التسارع سالب لأن اتجاهها معاكس لسرعتها التي هي موجبة.

الدلالة

السرعة النهائية أقل بكثير من السرعة الابتدائية، كما هو مطلوب عند التباطؤ، لكنها لا تزال موجبة (انظر الشكل). باستخدام المحركات النفاثة، يمكن الحفاظ على الدفع العكسي لفترة كافية لإيقاف الطائرة والبدء في تحريكها للخلف، وهو ما يشار إليه بسرعة نهائية سالبة، ولكن ليس هذا هو الحال هنا.

نتائج معادلة الحركة بتسارع ثابت

بالإضافة إلى كونها مفيدة في حل المسائل، فإن المعادلة v = v₀ + at تعطينا نظرة ثاقبة للعلاقات بين السرعة والتسارع والوقت. يمكننا أن نرى، على سبيل المثال، أن:

• تعتمد السرعة النهائية على مقدار التسارع الثابت ومدة استمراره.
• إذا كان التسارع صفرًا، فإن السرعة النهائية تساوي السرعة الابتدائية (v = v₀)، كما هو متوقع (بمعنى آخر، السرعة ثابتة أو منتظمة).
• إذا كان التسارع a سالب، تكون السرعة النهائية أقل من السرعة الابتدائية.

كل هذه الملاحظات تناسب حدسنا. لاحظ أنه من المفيد دائمًا فحص المعادلات الأساسية في ضوء حدسنا وخبرتنا للتحقق من أنها تصف الطبيعة بدقة بالفعل.

إيجاد الموضع النهائي مع الحركة بتسارع ثابت

يمكننا تجميع المعادلات السابقة لإيجاد معادلة ثالثة تسمح لنا بحساب الموضع النهائي لجسم ما يتحرك في تسارع ثابت. وذلك كما يلي:

v = v₀ + at

بإضافة v₀ إلى طرفي هذه المعادلة والقسمة على 2 نحصل على ما يلي:

(v + v₀) / 2 = v₀ + 1/2 (at)

وحيث أن:

(v₀ + v) / 2 = v

فيكون لدينا:

v = v₀ + 1/2 (at)

والآن نقوم بالتعويض من هذه المعادلة في معادلة حساب الإزاحة، لنحصل على الناتج كما يلي:

x = x₀ + v₀ t + 1/2 at² (constant a)

(3.13)

مثال 3.8: حساب إزاحة جسم يتحرك بتسارع ثابت

يمكن أن تحقق سيارة سباق تسارع متوسط يبلغ 26.0 م / ث². لنفترض أن سيارة السباق تتسارع من السكون على هذا المعدل لمدة 5.56 ثانية. (الشكل 3.20). إلى أي مدى سوف تتحرك في هذا الوقت؟

إستراتيجية الحل

أولاً، دعنا نرسم رسمًا تخطيطيًا (الشكل 3.21). مطلوب منا إيجاد الإزاحة، وهي x إذا اعتبرنا x₀ صفرًا. (فكر في x₀ على أنه خط البداية للسباق. يمكن أن يكون في أي مكان، لكننا نسميه صفر ونقيس كل المواضع الأخرى نسبيًا بالقياس بالنسبة له). يمكننا استخدام المعادلة x = x₀ + v₀ t + 1/2 at² عندما نحدد v₀ و a و t من
معطيات المسألة.

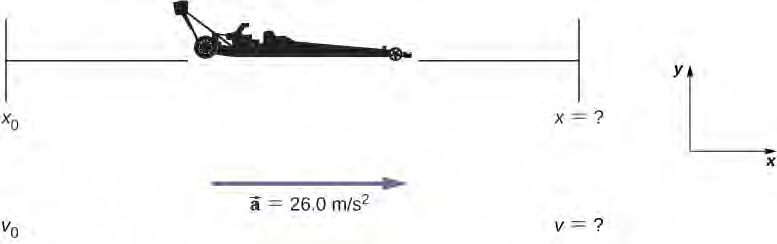
الحل

أولاً، نحتاج إلى تحديد الأشياء المعلومة. البدء من السكون يعني أن v₀ = 0. والتسارع a مُعطى بقيمة 26 متر/ث². والزمن t معطى بقيمة 5.56 ثانية.

ثانيًا، نعوض بالقيم المعلومة في المعادلة لإيجاد قيمة المجهول:

x = x₀ + v₀ t + 1/2 at²

نظرًا لأن الموضع الابتدائي والسرعة كلاهما صفر، فيمكن تبسيط هذه المعادلة إلى:

x = 1/2 at²

بالتعويض عن القيم المحددة لـ a و t ينتج لنا:

x = 1/2 * (26.0 m/s²) (5.56)² = 402 m

الدلالة

إذا قمنا بتحويل 402 متر إلى أميال، فسنجد أن المسافة المقطوعة قريبة جدًا من ربع ميل، وهي المسافة المعيارية لسباق دراج (Drag racing هو نوع من سباقات السيارات التي تتنافس فيها السيارات أو الدراجات البخارية، عادةً في سباقين في كل مرة، لتكون أول من يعبر خط النهاية المحدد). لذا، فإن إجابتنا معقولة. وهذه إزاحة رائعة يتم تغطيتها في 5.56 ثانية فقط، ولكن يمكن في السباق من الدرجة الأولى قطع مسافة ربع ميل في وقت أقل من ذلك. إذا بدأت السيارة بالحركة بسرعة ابتدائية بدلا من البدء من حالة السكون، فهذا سيضيف حدًا آخر إلى معادلة حساب المسافة. إذا تم استخدام نفس التسارع والوقت في المعادلة، فإن المسافة المقطوعة ستكون أكبر بكثير.

ما الذي يمكننا تعلمه أيضًا من خلال فحص المعادلة x = x₀ + v₀ t +1/2 at²؟ يمكننا أن نرى العلاقات التالية:

تعتمد الإزاحة على مربع الوقت المنقضي عندما لا يكون التسارع صفرًا. في المثال السابق، قطعت سيارة السباق ربع المسافة الإجمالية فقط في النصف الأول من الوقت المنقضي

إذا كان التسارع صفرًا، فإن السرعة الابتدائية تساوي السرعة المتوسطة (v₀ = v)، والمعادلة:

x = x₀ + v₀ t + 1/2 at²

تصبح كما يلي:

x = x₀ + v₀ t

إيجاد السرعة النهائية من المسافة والتسارع

يمكن الحصول على معادلة رابعة مفيدة من معالجة جبرية أخرى للمعادلات السابقة. إذا حللنا المعادلة بالنسبة ل t:

v = v₀ + a t

نحصل على:

t = ( v – v₀ ) / a

كما لدينا المعادلة:

(v₀ + v) / 2 = v

والآن بالتعويض عن هاتين المعادلتين في المعادلة:

x = x₀ + v t

نحصل على المعادلة التالية:

v² = v₀² + 2 a (x – x₀) …. (constant a)

(3.14)

مثال 3.9: حساب السرعة النهائية

احسب السرعة النهائية للسائق في المثال 3.8 بدون استخدام معلومات الوقت (أو الزمن).

إستراتيجية الحل

المعادلة v² = v₀ ² + 2a (x – x₀) مناسبة بشكل مثالي لهذه المهمة لأنها تتعلق بالسرعات والتسارع والإزاحة، وليس هناك حاجة لمعلومات الوقت.

الحل

أولاً، نحدد القيم المعلومة. نحن نعلم أن v₀ = 0، لأن السائق يبدأ من السكون. ونعلم أيضًا أن x – x₀ = 402، (كان هذا هو الجواب في المثال 3.8). كما تم إعطاء متوسط التسارع على أنه a = 26.0 m / s².

ثانيًا، نقوم الآن بالتعويض عن القيم المعلومة في المعادلة v² = v₀ ² + 2a (x – x₀) ونحلها من أجل إيجاد قيمة السرعة النهائية v:

الدلالة

تبلغ السرعة التي مقدارها 145 متر / ثانية حوالي 522 كم / ساعة، أو حوالي 324 ميل / ساعة، ولكن حتى هذه السرعة الفائقة أقل من سرعة الرقم القياسي العالمي للربع ميل. لاحظ أيضًا أن الجذر التربيعي له قيمتان؛ أخذنا القيمة الموجبة للإشارة إلى السرعة في نفس اتجاه التسارع.

يمكن أن ينتج عن فحص المعادلة v² = v₀ ² + 2a (x – x₀) رؤى إضافية في العلاقات العامة بين الكميات الفيزيائية:

• السرعة النهائية تعتمد على مقدار التسارع والمسافة التي يعمل خلالها.
• في حالة ثبات التسارع، فإن السيارة التي تسير بسرعة مضاعفة لا تتوقف بسهولة في ضعف المسافة. بل أنها تتطلب مسافة أكبر للوصول إلى حالة التوقف. ولهذا السبب يتم وضع إشارات المرور لتقليل السرعة بالقرب من المدارس.

ملخص قوانين الحركة مع تسارع ثابت

في الأمثلة التالية، يتم استكشاف الحركة أحادية البعد من خلال معادلات محددة، وفي كثير من المواقف قد يتطلب الأمر معالجة جبرية أكثر تعقيدًا قليلاً. تغطي معظم الأمثلة التالية نظرة ثاقبة على تقنيات حل المسائل المتنوعة. والملخص التالي لمعادلات الحركة مع تسارع ثابت يهدف إلى تسهيل الرجوع إلى المعادلات المطلوبة من أجل حل تلك المسائل. وهذه المعادلات ليست مستقلة. في كثير من الحالات يكون لدينا مجهولين اثنين ونحتاج إلى معادلتين من هذه المجموعة لإيجاد قيمة المجهول. وتذكر دائمًا أننا نحتاج إلى عدد من المعادلات يساوي عدد المجاهيل من أجل حلها وإيجاد قيمتها في أي مسألة معينة. فيما يلي ملخص المعادلات:

x = x₀ +v t

v = v₀ + at

ملاحظات

قبل أن ندخل في الأمثلة، دعنا نلقي نظرة على بعض المعادلات عن كثب لنرى سلوك التسارع عند القيم القصوى. من خلال إعادة ترتيب المعادلة 3.12، يمكننا التعبير عن التسارع كما يلي:

a = ( v – v₀ ) / t

من هذا، نرى أنه، لفترة زمنية محدودة، إذا كان الفرق بين السرعتين الابتدائية والنهائية صغيرًا، فإن العجلة أو التسارع يكون صغير، وهو يقترب من الصفر عند الحد الذي تتساوى فيه السرعتان الابتدائية والنهائية. على العكس من ذلك، في النهاية التي تصل فيها قيمة الزمن للصفر t → 0 وللفرق النهائي بين السرعة الابتدائية والسرعة والنهائية، يصبح التسارع لانهائيًا.

وبالمثل، بإعادة ترتيب المعادلة 3.14، يمكننا التعبير عن التسارع بدلالة السرعات والإزاحة كما يلي:

a = (v² − v₀²) / 2 (x − x₀)

ومن هذه المعادلة يمكن استنتاج أنه بالنسبة للفرق المحدود بين السرعات الابتدائية والنهائية، يصبح التسارع غير محدود عندما تقترب الإزاحة من الصفر (لأن الإزاحة موجودة في المقام). كذلك يقترب التسارع من الصفر كلما اقترب الفرق بين السرعة الابتدائية والنهائية من الصفر، بالنسبة لإزاحة محدودة.

مثال 3.10: إلى أي مدى تذهب السيارة؟

على الخرسانة الجافة، يمكن أن تتباطأ السيارة بمعدل 7 متر / ثانية²، بينما على الخرسانة الرطبة يمكن أن تتباطأ بمعدل 5 متر / ثانية² فقط. أوجد المسافات اللازمة لإيقاف حركة السيارة التي تسير بسرعة 30 متر / ثانية (حوالي 110 كم / ساعة) على (أ) الخرسانة الجافة و(ب) الخرسانة الرطبة. (ج) كرر كلا الحسابين وابحث عن الإزاحة من النقطة التي يرى فيها السائق إشارة المرور تتحول إلى اللون الأحمر، مع مراعاة وقت رد فعله البالغ 0.5 ثانية لوضع قدمه على الفرامل.

إستراتيجية الحل

أولاً، نحتاج إلى رسم رسم تخطيطي للشكل 3.22. لتحديد المعادلات الأفضل استخدامًا ، نحتاج إلى سرد جميع القيم المعروفة وتحديد ما نحتاج إلى حله بالضبط.

الحل

أ. الحالة الأولى السير على الخرسانة الجافة

أولاً، نحتاج إلى تحديد المعطيات المعلومة والمجاهيل المطلوب إيجادها. نعلم أن السرعة الابتدائية v₀ =30 m/s. ونعلم أن السرعة النهائية عند التوقف v = 0. كما نعلم أن a = -7 m/s² (a بإشارة سالبة لأنه تباطؤ وفي اتجاه معاكس للسرعة). نحدد قيمة x₀ على أنه صفر. والمطلوب إيجاد الإزاحة Δx أو x – x₀.

ثانيًا، نحدد المعادلة التي ستساعدنا في حل المسألة. أفضل معادلة لاستخدامها هي:

v² = v₀ ² + 2a (x – x₀)

هذه المعادلة هي الأفضل لأنها تتضمن مجهولا واحدًا غير معروف وهو x. نعرف قيم جميع المتغيرات الأخرى في هذه المعادلة. (ستسمح لنا المعادلات الأخرى بإيجاد قيمة x، لكنها تتطلب منا معرفة الزمن اللازم للتوقف t، وهو الذي لا نعرفه. يمكننا استخدامها، ولكنها تتطلب حسابات إضافية).

ثالثًا، نعيد ترتيب المعادلة لإيجاد قيمة x كما يلي:

( x – x₀ ) = ( v² – v₀ ² ) / 2a

بالتعويض عن القيم المعلومة:

( x – 0 ) = 0 ² – ( 30 m/s ² ) / 2 ( – 7 m / s² )

وبالتالي تكون المسافة التي تقطعها السيارة على الخرسانة الجافة حتى تتوقف هي:

x = 64.3 m

ب. الحالة الثانية: السير على الخرسانة الرطبة

يمكن حل هذا الجزء بنفس الطريقة تمامًا مثل (أ). الفرق الوحيد هو أن العجلة أو التسارع في هذه الحالة يساوي −5 متر / ثانية ². والنتيجة هي:

المسافة التي تقطعها السيارة على الخرسانة الرطبة حتى تتوقف هي:

x = 90 m

ج. عندما يتفاعل السائق بالضغط على الفرامل:

عندما يتفاعل السائق مع الضغط على الفرامل، تكون مسافة التوقف هي نفسها الموجودة في الحالتين (أ) و(ب) للخرسانة الجافة والرطبة.

إذن، للإجابة على هذا السؤال، نحتاج إلى حساب المسافة التي تقطعها السيارة خلال وقت رد الفعل، ثم نضيف ذلك إلى وقت التوقف. من المعقول أن نفترض أن السرعة تظل ثابتة أثناء وقت رد فعل السائق.

للقيام بذلك، مرة أخرى، نحدد القيم المعلومة والقيم المجهولة التي نريد إيجاد قيمتها. نعلم أن v = 30 m / s، وزمن رد الفعل t _reaction = 0.5 s ، وتسارع رد الفعل a _reaction = 0. نأخذ x_0-reaction ليكون صفرًا. نحن نبحث عن x_reaction.

ثانيًا، كما في السابق، نحدد أفضل معادلة يمكن استخدامها. في هذه الحالة، x = x₀ + v t تعمل بشكل جيد لأن القيمة الوحيدة غير المعروفة هي x، وهو ما نريد إيجاده.

ثالثًا، بالتعويض عن قيمة الأشياء المعلومة لحل المعادلة:

x = 0 + (30.0 m/s)(0.5 s) = 15 m

هذا يعني أن السيارة تسير مسافة 15 مترًا بينما يتفاعل السائق مع الضغط على الفرامل، مما يجعل إجمالي الإزاحتان في حالتي السير على الخرسانة الجافة والرطبة أكبر بمقدار 15 مترًا مما لو تفاعل على الفور.

التعويض عن القيم

أخيرًا، نضيف الإزاحة أثناء وقت رد الفعل إلى الإزاحة عند الضغط على الفرامل (الشكل 3.23):

x_braking + x_reaction = x_total

ونجد أن (أ) تكون 64.3 م + 15.0 م = 79.3 م عندما تكون الخرسانة جافة و(ب) تكون 90.0 م + 15.0 م = 105 م عندما تكون الخرسانة رطبة.

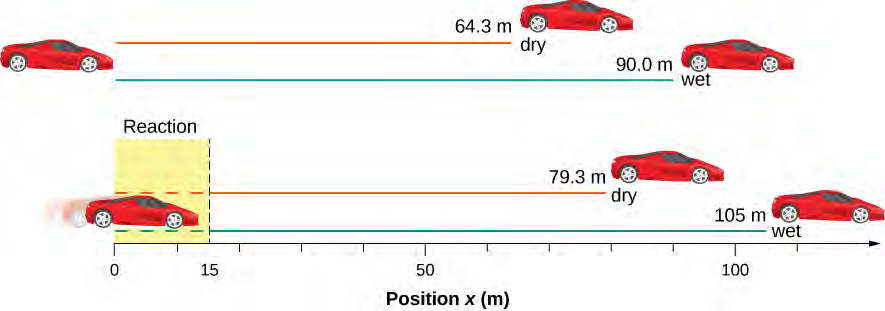
الشكل 3.23 تختلف المسافة اللازمة لإيقاف السيارة اختلافًا كبيرًا، اعتمادًا على حالة الطريق ووقت رد فعل السائق. تظهر هنا مسافات الكبح للأرصفة الجافة والرطبة، كما تم حسابها في هذا المثال، لسيارة تسير مبدئيًا بسرعة 30.0 م / ث. يظهر أيضًا إجمالي المسافات التي تم قطعها من النقطة التي رأى فيها السائق أ الضوء يتحول إلى اللون الأحمر، بافتراض أن وقت رد الفعل يبلغ 0.500 ثانية.

الدلالة

يبدو أن الإزاحة الموجودة في هذا المثال معقولة لإيقاف سيارة سريعة الحركة. يجب أن يستغرق إيقاف السيارة على الرصيف الرطب أو المبلل وقتًا أطول من الوقت اللازم لإيقافها على طريق جاف. من المثير للاهتمام أن وقت رد الفعل يضيف بشكل كبير إلى حسابات المسافة، ولكن الأهم من ذلك هو النهج العام لحل المسائل. نحدد الكميات المعلومة والكميات المراد إيجادها، ثم نجد المعادلة المناسبة. إذا كان هناك أكثر من مجهول غير معروف، فنحن بحاجة إلى العديد من المعادلات المستقلة حيث يوجد عدد غير معروف لحلها. غالبًا ما توجد أكثر من طريقة لحل مسألة ما. في الواقع، يمكن حل الأجزاء المختلفة من هذا المثال بطرق أخرى، لكن الحلول المقدمة هنا هي الأقصر.

مثال 3.11: حساب الزمن

لنفترض أن سيارة اندمجت في حركة المرور على الطريق السريع على منحدر طوله 200 متر. إذا كانت سرعتها الابتدائية 10 متر / ثانية وتسارعت بمقدار 2 متر / ثانية ²، فكم من الوقت تستغرق السيارة لتقطع مسافة 200 متر أعلى المنحدر؟ (قد تكون هذه المعلومات مفيدة لمهندس المرور).

إستراتيجية الحل

أولًا، نرسم رسمًا تخطيطيًا (الشكل 3.24)، والمطلوب منا إيجاد الزمن أو الوقت t. كما كان من قبل، نحدد الكميات المعلومة لاختيار علاقة مادية مناسبة (أي معادلة مع متغير غير معروف واحد وهو هنا t).

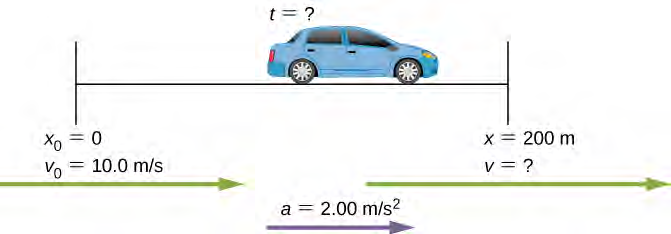
الحل

مرة أخرى، نحدد الأشياء المعلومة والمجهول الذي نريد إيجاده. نعلم أن:

x₀ = 0

v₀ = 10 m/s

a = 2 m/s²

x = 200 m

علينا إيجاد قيمة t. تعمل المعادلة x = x₀ + v₀ t + 1/2 at² بشكل أفضل لأن المجهول الوحيد في المعادلة هو المتغير t، والذي نحتاج إلى إيجاده. من هذه الرؤية، نرى أنه عندما نقوم بإدخال العناصر المعلومة في المعادلة، فإننا ننتهي بمعادلة تربيعية.

نحتاج إلى إعادة ترتيب المعادلة لإيجاد قيمة t، ثم التعويض عن العناصر المعلومة في المعادلة:

x = x₀ + v₀ t + 1/2 at²

200 m = 0 m + (10 m/s) t + 1/2 ( 2 t² )

ثم نبسط المعادلة. تلغي وحدات المتر لأنها موجودة في كل حدود المعادلة (عن طريق القسمة على m). يمكننا أن نحذف وحدات الثواني بالضرب في s لنحصل على النتيجة بالثواني، أي بوضع t = t s، حيث t هي مقدار الزمن و s هي وحدة قياس الزمن بالثواني. القيام بذلك يترك لنا:

200 = 10 t + t²

ثم نستخدم الصيغة التربيعية لإيجاد قيمة t:

t² + 10 t – 200 = 0

t = {-b + Sqr (b2 – 4ac)} / 2a

والذي ينتج حلين: t = 10 و t = −20. القيمة السالبة للوقت غير معقولة، لأنها تعني أن الحدث وقع قبل 20 ثانية من بدء الحركة. يمكننا تجاهل هذا الحل. هكذا يكون الحل المنطقي هو: t = 10 ثانية.

الدلالة

عندما تحتوي المعادلة على قيمة مربعة غير معلومة، فهناك حلان. يكون كلا الحلين مفيدًا في بعض المسائل؛ في حالات أخرى، حل واحد فقط هو المعقول. تبدو الإجابة 10 ثانية معقولة بالنسبة لطريق سريع نموذجي على منحدر.

تحقق من فهمك

يتسارع صاروخ مأهول بمعدل 20 متر / ثانية ² أثناء الإطلاق. كم من الوقت يستغرق الصاروخ للوصول إلى سرعة 400 متر / ثانية؟

يتسارع صاروخ مأهول بمعدل 20 متر / ثانية ² أثناء الإطلاق. كم من الوقت يستغرق الصاروخ للوصول إلى سرعة 400 متر / ثانية؟

مثال 3.12: تسريع المركبة الفضائية

غادرت مركبة فضائية مدار الأرض وهي في طريقها إلى القمر. بتسارع بمعدل 20 متر / ثانية ² لمدة دقيقتين ولمسافة 1000 كم. ما هي السرعات الابتدائية والنهائية لسفينة الفضاء؟

إستراتيجية الحل

مطلوب منا إيجاد السرعات الابتدائية والنهائية لسفينة الفضاء. بالنظر إلى معادلات الحركة، نرى أن معادلة واحدة لن تعطي الإجابة. يجب أن نستخدم معادلة حركة واحدة لإيجاد إحدى السرعات والتعويض عنها في معادلة حركة أخرى للحصول على السرعة الثانية. وهكذا، نحل اثنتين من معادلات الحركة في وقت واحد.

الحل

نحل أولاً من أجل إيجاد قيمة السرعة الابتدائية v₀ باستخدام المعادلة:

x = x₀ + v₀ t +1/2 at²

x – x₀ = v₀ t +1/2 at²

بالتعويض عن القيم المعلومة:

1.0 × 10⁶ m = v₀ (120 s) + 1/2 (20 m/s²)(120 s)²

v₀ = 7133.3 m/s

ثم نقوم بالتعويض عن v₀ في المعادلة v = v₀ + at لإيجاد السرعة النهائية:

v = v₀ + at = 7133.3 m/s + (20 m/s²)(120 s) = 9533.3 m/s

الدلالة

هناك ست متغيرات في الإزاحة والوقت والسرعة والتسارع تصف الحركة في بُعد واحد. يمكن أن تكون الشروط أو المعطيات الأولية لمسألة معينة عبارة عن مجموعات عديدة من هذه المتغيرات. بسبب هذا التنوع، قد لا تكون الحلول سهلة مثل التعويض البسيط في إحدى المعادلات. يوضح هذا المثال أن حلول علم الحركة قد تتطلب حل معادلتين حركيتين متزامنتين أي في نفس الوقت.

بعد تعلم أساسيات علم الحركة، يمكننا الانتقال إلى العديد من الأمثلة والتطبيقات الأخرى المثيرة للاهتمام. في عملية تطوير علم الحركة، لقد لمحنا أيضًا نهجًا عامًا لحل المسائل ينتج عنه إجابات صحيحة ورؤى ثاقبة في العلاقات المادية. يتضمن المستوى التالي من التعقيد في مسائل علم الحركة لدينا حركة جسمين مترابطين، تسمى مسائل المطاردة بين جسمين.

مسائل المطاردة بين جسمين

حتى هذه النقطة، نظرنا في أمثلة للحركة التي تنطوي على جسم واحد. حتى بالنسبة لمسألة حول حركة سيارتين ومسافات التوقف على الطرق الرطبة والجافة، قمنا بتقسيم هذه المسألة إلى مسألتين منفصلتين للعثور على الإجابات.

في مسألة المطاردة ثنائية الجسم أو بين جسمين، تقترن حركات الأشياء معًا، بمعنى أن المجهول الذي نسعى إلى إيجاد قيمته يعتمد على حركة كلا الجسمين. لحل هذه المسائل، نكتب معادلات الحركة لكل كائن ثم نحلها معًا في نفس الوقت لإيجاد القيمة المجهولة. هذا موضح في الشكل 3.25.

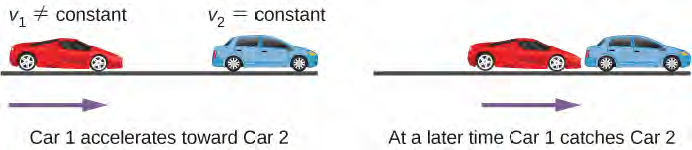
يعتمد الوقت والمسافة اللازمتان للسيارة 1 للحاق بالسيارة 2 على المسافة الأولية بين السيارة 1 والسيارة 2 بالإضافة إلى سرعات كلتا السيارتين وتسارع السيارة 1. يجب حل المعادلات الحركية التي تصف حركة كلتا السيارتين للعثور على هذه القيم المجهولة.

المثال التالي يوضح هذه المسألة.

مثال 3.14: الفهد يصطاد الغزال

فهد ينتظر مختبئًا خلف الأدغال. يكتشف الفهد غزالًا يمر بسرعة 10 م / ث. في اللحظة التي يمر فيها الغزال من الفهد، يتسارع الفهد من السكون بعجلة مقدارها 4 م / ث ² للإمساك بالغزال. (أ) ما هي المدة التي يستغرقها الفهد للإمساك بالغزال؟ (ب) ما هي إزاحة الغزال والفهد؟

إستراتيجية الحل

نستخدم مجموعة معادلات الحركة بتسارع ثابت لحل هذه المسألة. نظرًا لوجود كائنين متحركين، فلدينا معادلات منفصلة للحركة تصف كل حيوان. لكن ما يربط المعادلات هو عامل مشترك له نفس القيمة لكل حيوان. إذا نظرنا إلى المسألة عن كثب، فمن الواضح أن العامل المشترك لكل حيوان هو موقعه x في وقت لاحق بعد مدة زمنية مقدارها t. نظرًا لأن كلاهما يبدأ عند x₀ = 0، فإن إزاحتهما هي نفسها في وقت لاحق t، عندما يلحق الفهد بالغزال. إذا اخترنا معادلة الحركة التي تستخدم لإيجاد الإزاحة لكل حيوان، فيمكننا حينئذٍ تعيين المعادلتين على أنهما متساويتين وإيجاد المجهول، وهو الوقت t.

الحل

أ. معادلة الغزال: للغزال سرعة ثابتة وهي متوسط ​​سرعته لأنه لا يتسارع. لذلك، نستخدم المعادلة رقم 3.10 مع x₀ = 0:

x = x₀ + v t = v t

معادلة الفهد: الفهد يتسارع من السكون، لذلك نستخدم المعادلة 3.13 مع x₀ = 0 وv₀ = 0:

x = x₀ + v₀ t +1/2 at² = 1/2 at²

الآن لدينا معادلة الحركة لكل حيوان بعامل مشترك، والذي يمكن حذفه لإيجاد الحل. في هذه الحالة، نحل المعادلتين لإيجاد قيمة t:

x = v t = 1/2 at²

t = 2 v / a

سرعة الغزال ثابتة بقيمة 10 م / ث، وهي سرعته المتوسطة. تسارع الفهد هو 4 م / ث ². بالتعويض في المعادلة وحساب الوقت الذي يستغرقه وصول الفهد إلى الغزال، يكون لدينا:

t = 2 (10) / 4 = 5 seconds

ب. للحصول على الإزاحة، نستخدم إما معادلة الحركة للفهد أو الغزال، حيث يجب أن يعطيا نفس الإجابة.

إزاحة الفهد:

x = 1/2 at² = 1/2 (4) (5)² = 50 m

إزاحة الغزال:

x = v t = (10) (5) = 50 m

نرى أن كلا الإزاحتين متساويتين، كما هو متوقع.

الدلالة

من المهم تحليل حركة كل كائن واستخدام المعادلات الحركية المناسبة لوصف الحركة الفردية له. من المهم أيضًا أن يكون لديك منظور بصري جيد لمسائل مطاردة الجسمين لرؤية العوامل المشتركة التي تربط حركة كلا الجسمين.

تحقق من فهمك

للدراجة سرعة ثابتة مقدارها 10 م / ث. يبدأ شخص من السكون ويركض للحاق بالدراجة في 30 ثانية. ما هو تسارع الشخص؟

المصدر

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.