الحركة في خط مستقيم – الحركة في بُعد واحد

الشكل 3.1: قطار ماجليف (رفع مغناطيسي) من سلسلة JR Central L0 المكون من خمس عربات يخضع للتشغيل التجريبي على مسار اختبار Yamanashi. يمكن وصف حركة القطار المغناطيسي باستخدام علم الحركة Kinematics، وهو موضوع هذا الفصل بعنوان الحركة في خط مستقيم – الحركة في بُعد واحد.
مخطط الفصل
- 3.1 الموضع، والإزاحة، والسرعة المتوسطة
- 3.2 السرعة اللحظية والسرعة المتوسطة
- 3.3 التسارع – متوسط التسارع والتسارع اللحظي
- 3.4 الحركة مع التسارع المنتظم
- 3.5 السقوط الحر
- 3.6 معادلات الحركة والتفاضل والتكامل
المحتويات
علم الحركة في خط مستقيم أو الحركة في بُعد واحد
كوننا مليء بالأشياء المتحركة، من حركة النجوم والكواكب والمجرات إلى حركة الناس والحيوانات، وصولاً إلى النطاق المجهري للذرات والجزيئات، كل شيء في كوننا في حالة حركة. يمكننا وصف الحركة باستخدام تخصصي علم الحركة Kinematics والديناميكا Dynamics. ندرس الديناميكا، التي تهتم بأسباب الحركة، في قوانين نيوتن للحركة؛ ولكن هناك الكثير لنتعلمه عن الحركة دون الرجوع إلى أسبابها، وهذه هي دراسة علم الحركة أو الكينماتيكا Kinematics. يتضمن علم الحركة وصف الحركة من خلال خصائص مثل الموضع والزمن والسرعة والتسارع.
العلاج الكامل لعلم الحركة يعتبر الحركة في بعدين وثلاثة أبعاد. في الوقت الحالي، نناقش الحركة في خط مستقيم أو الحركة في بُعد واحد، مما يوفر لنا الأدوات اللازمة لدراسة الحركة متعددة الأبعاد في الفصول التالية. من الأمثلة الجيدة على كائن يمر بحركة أحادية الأبعاد قطار ماجليف (الرفع المغناطيسي) الموضح في بداية هذا الفصل. بينما يسافر، على سبيل المثال، من طوكيو إلى كيوتو، يكون في مواقع مختلفة على طول المسار في أوقات مختلفة في رحلته، وبالتالي يكون لديه نزوح، أو تغيرات في الموضع. كما أن لديه مجموعة متنوعة من السرعات على طول مساره ويخضع لتسارع (تغيرات في السرعة).
بالمهارات المكتسبة في هذا الفصل يمكننا حساب هذه الكميات ومتوسط السرعة. يمكن وصف كل هذه الكميات باستخدام علم الحركة، دون معرفة كتلة القطار أو القوى المعنية بتسييره.
الموضع والإزاحة والسرعة المتوسطة
الأهداف: بنهاية هذا القسم، سيكون القارئ قادرًا على:
- تحديد الموضع والإزاحة والمسافة المقطوعة.
- حساب الإزاحة الكلية مع الأخذ في الاعتبار الموضع كدالة للزمن.
- تحديد إجمالي المسافة المقطوعة.
- حساب السرعة المتوسطة بالنظر إلى الإزاحة والزمن المنقضي.
عندما تكون في حالة حركة، فإن الأسئلة الأساسية التي يجب طرحها هي: أين أنت؟ إلى أين تذهب؟ ما مدى سرعة الوصول إلى هناك؟ تتطلب إجابات هذه الأسئلة أن تحدد موقعك أو موضعك، والإزاحة، ومتوسط السرعة، وهي المصطلحات التي نتعرف عليها في هذا القسم.
الموضع
لوصف حركة كائن ما، يجب أولاً أن تكون قادرًا على وصف موضعه (س): مكانه في أي وقت معين.
بتعبير أدق، نحتاج إلى تحديد موضعه Position بالنسبة إلى إطار مرجعي مناسب. الإطار المرجعي عبارة عن مجموعة عشوائية من المحاور يتم من خلالها وصف موضع وحركة كائن ما. غالبًا ما يتم استخدام الأرض كإطار مرجعي، وغالبًا ما نصف موضع كائن من حيث صلته بالأجسام الثابتة على الأرض. على سبيل المثال، يمكن وصف إطلاق الصاروخ من حيث موضع الصاروخ بالنسبة إلى الأرض ككل، في حين يمكن وصف موضع راكب الدراجة من حيث مكان وجوده بالنسبة للمباني التي يمر بها الشكل 3.2. في حالات أخرى، نستخدم إطارات مرجعية ليست ثابتة ولكنها متحركة بالنسبة إلى الأرض. لوصف موقع شخص ما في طائرة، على سبيل المثال، نستخدم الطائرة، وليس الأرض، كإطار مرجعي. لوصف موضع كائن يمر بحركة أحادية الأبعاد أو في بعد واحد أو الحركة في خط مستقيم، غالبًا ما نستخدم المتغير الأفقي x. لاحقًا في الفصل، أثناء مناقشة السقوط الحر، نستخدم المتغير الرأسي y.

الشكل 3.2: يمكن وصف راكبي الدراجات في فيتنام من خلال موقعهم بالنسبة للمباني أو القناة. يمكن وصف حركتهم من خلال تغيير موضعهم، أو إزاحتهم، في إطار مرجعي. (الصورة: تعديل عمل سوزان بلاك).
الإزاحة
إذا كان كائن يتحرك بالنسبة إلى إطار مرجعي – على سبيل المثال، إذا انتقل أستاذ إلى اليمين بالنسبة إلى السبورة البيضاء الشكل 3.3 – فحينئذٍ يتغير موضع الكائن. هذا التغيير في الموضع يسمى الإزاحة Displacement. تشير كلمة الإزاحة إلى أن الجسم قد تحرك أو تم إزاحته. على الرغم من أن الموضع هو القيمة العددية لـ x على طول خط مستقيم حيث يمكن أن يوجد كائن، فإن الإزاحة تعطي التغيير في الموضع على طول هذا الخط. نظرًا لأن الإزاحة تشير إلى الاتجاه، فهي كمية متجهة ويمكن أن تكون موجبة أو سالبة، اعتمادًا على اختيار الاتجاه الموجب. أيضًا، يمكن أن يحتوي تحليل الحركة على العديد من عمليات الإزاحة المضمنة فيه. إذا كان اتجاه اليمين موجبًا وكان الجسم يتحرك بمقدار 2 متر إلى اليمين، ثم 4 متر إلى اليسار، فإن الإزاحة الفردية تكون 2 متر و-4 متر، على التوالي.
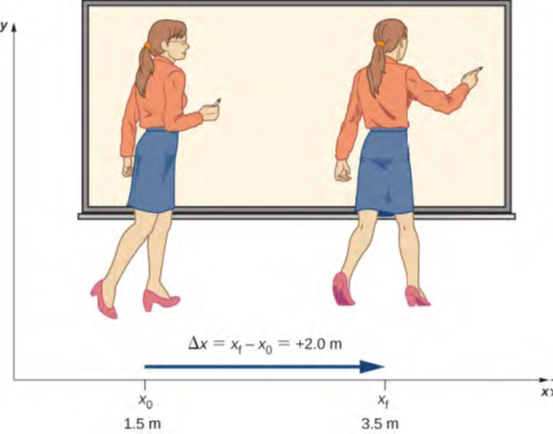
الشكل 3.3: يسير الأستاذ يسارًا ويمينًا أثناء إلقاء المحاضرة. يتم تحديد موقعه بالنسبة إلى الأرض بواسطة x. يتم تمثيل إزاحة الأستاذ بالقيمة +2.0 m بالنسبة إلى الأرض بواسطة سهم يشير إلى اليمين.
معادلة حساب الإزاحة
الإزاحة Δx هي التغيير في موضع كائن ما، حيث:
Δx = xf − x0
(3.1)
حيث Δx هي الإزاحة، و xf هو الموضع النهائي Final، و x0 هو الموضع الأولي Origun.
نستخدم الحرف اليوناني الكبير دلتا (Δ) ليعني “التغيير” مهما كانت الكمية التي تليها؛ وبالتالي، فإن Δx تعني التغيير في الموضع (الموضع النهائي مطروحًا منه الموضع الأولي). نحل دائمًا إيجاد الإزاحة بطرح الموضع الأولي x0 من الموضع النهائي xf. لاحظ أن وحدة النظام الدولي للوحدات للإزاحة هي المتر، لكن في بعض الأحيان نستخدم الكيلومترات أو وحدات الطول الأخرى.
ضع في اعتبارك أنه عند استخدام وحدات أخرى غير الأمتار في مسألة ما، فقد تحتاج إلى تحويلها إلى أمتار لإكمال الحساب (انظر الملحق ب).
يمكن أن تحتوي الكائنات المتحركة أيضًا على سلسلة من عمليات الإزاحة. في المثال السابق لحركة الأستاذ، تكون الإزاحات الفردية 2 متر و-4 متر، مما يعطي إزاحة إجمالية قدرها 2 متر. نحدد الإزاحة الإجمالية ΔxTotal، كمجموع حالات الإزاحات الفردية، ونعبر عن ذلك رياضيًا بالمعادلة التالية:
Δx Total = Σ Δxi
(3.2)
حيث Δxi هي عمليات النزوح الفردية. في المثال السابق، يكون:
Δx1 = x1 − x0 = 2 − 0 = 2 m
وبالمثل:
Δx2 = x2 − x1 = −2 − (2) = −4 m
الإزاحة الكلية
وبالتالي تكون الإزاحة الكلية:
ΔxTotal = Δx1 + Δx2 = 2 − 4 = −2 m
الإزاحة الكلية هي 2-4 = −2 متر إلى اليسار أو في الاتجاه السالب. من المفيد أيضًا حساب مقدار الإزاحة أو قيمتها. دائمًا ما يكون مقدار الإزاحة موجبًا. هذه هي القيمة المطلقة للإزاحة، لأن الإزاحة متجه ولا يمكن أن تكون لها قيمة سالبة من حيث المقدار. في مثالنا، مقدار الإزاحة الإجمالية 2 متر، في حين أن مقادير النزوح الفردي هي 2 متر و4 متر.
لا ينبغي الخلط بين مقدار الإزاحة الكلية والمسافة المقطوعة. المسافة المقطوعة xTotal، هي الطول الإجمالي للمسار الذي يتم قطعه بين موضعين. في المسألة السابقة، المسافة المقطوعة هي مجموع مقادير النزوح الفردي:
xTotal = |Δx1| + |Δx2| = 2 + 4 = 6 m
السرعة المتوسطة
لحساب الكميات الفيزيائية الأخرى في علم الحركة، يجب علينا تقديم متغير الزمن أو الوقت. لا يسمح لنا متغير الوقت فقط بتحديد مكان الكائن (موضعه) أثناء حركته، ولكن أيضًا مدى سرعة تحركه. يتم تحديد مدى سرعة تحرك الجسم من خلال المعدل الذي يتغير به الموضع مع مرور الوقت.
لكل موضع xi، نخصص وقتًا معينًا ti. إذا كانت تفاصيل الحركة في كل لحظة غير مهمة، فعادة ما يتم التعبير عن المعدل على أنه السرعة المتوسطة Average Velocity ويرمز لها بالرمز v. الكمية المتجهة هذه هي ببساطة الإزاحة الإجمالية بين نقطتين مقسومة على الوقت المستغرق للانتقال بينهما. الوقت المستغرق للسفر بين نقطتين يسمى الوقت المنقضي Δt.
معادلة حساب السرعة المتوسطة
إذا كانت x1 و x2 هي مواضع كائن ما في الأوقات t1 و t2 على التوالي، إذن يكون:
السرعة المتوسطة = v = الإزاحة بين النقطتين ÷ الوقت المنقضي للانتقال بين النقطتين
v =Δx /Δt = (x2 − x1) / (t2 − t1)
(3.3)
من المهم ملاحظة أن السرعة المتوسطة عبارة عن متجه ويمكن أن تكون سالبة، اعتمادًا على الموضعين x1 وx2.
مثال3.1 على الحركة في خط مستقيم: تسليم النشرات
تنطلق جيل من منزلها لتسليم منشورات لبيع فناء منزلها، مسافرة شرقًا على طول شارعها الذي تصطف على جانبيه المنازل.
بعد أن سارت مسافة 0.5 كيلومتر خلال 9 دقائق، نفدت النشرات وعليها أن تعيد خطواتها إلى منزلها للحصول على المزيد. يستغرق هذا الأمر 9 دقائق إضافية. بعد أن حصلت على المزيد من المنشورات، انطلقت مرة أخرى على نفس المسار، واستمرت من حيث توقفت، وانتهى بها الأمر على بعد كيلومتر واحد من منزلها. تستغرق هذه المحطة الثالثة من رحلتها 15 دقيقة. عند هذه النقطة تستدير عائدة نحو منزلها متجهة غربًا. بعد 1.75 كلم و25 دقيقة توقفت لتستريح.
- ما هو إجمالي إزاحة جيل إلى النقطة التي تتوقف عندها للراحة؟
- ما مقدار الإزاحة الكلية؟
- ج. ما هي السرعة المتوسطة خلال رحلتها بأكملها؟
- د. ما هي المسافة الإجمالية المقطوعة؟
- ه. قم بعمل رسم بياني للموضع مقابل الوقت.
يظهر رسم تخطيطي لحركات جيل في الشكل 3.4.
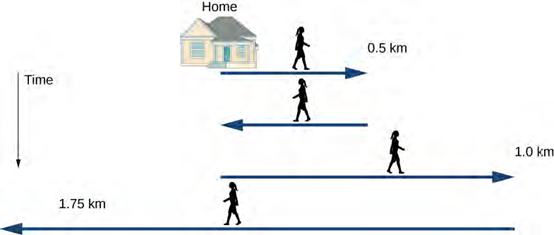
إستراتيجية الحل
تحتوي المسألة على بيانات حول مختلف مراحل رحلة جيل، لذلك سيكون من المفيد عمل جدول بالكميات الفيزيائية أو المادية. لقد تم تحديد المكان والوقت في صياغة المسألة حتى نتمكن من حساب الإزاحة والوقت المنقضي. نأخذ الشرق ليكون الاتجاه الإيجابي أو الموجب. من هذه المعلومات يمكننا إيجاد الإزاحة الكلية والسرعة المتوسطة. منزل جيل هو نقطة البداية x0. يوضح الجدول التالي الوقت ومكان جيل في أول عمودين، ويتم حساب الإزاحة في العمود الثالث.
| Displacement Δxi (km) | Position xi (km) | Time ti (min) |
| Δx0 = 0 | x 0 = 0 | t 0 = 0 |
| Δx1 = x1 − x0 = 0.5 | x 1 = 0.5 | t 1 = 9 |
| Δx2 = x2 − x1 = − 0.5 | x 2 = 0 | t 2 = 18 |
| Δx3 = x3 − x2 = 1.0 | x 3 = 1.0 | t 3 = 33 |
| Δx4 = x4 − x3 = − 1.75 | x 4 = – 0.75 | t 4 = 58 |
الحل
1. من الجدول أعلاه، فإن إجمالي الإزاحة هو:
Σ Δxi = 0.5 − 0.5 + 1.0 − 1.75 km = − 0.75 km
2. مقدار الإزاحة الكلية هو | −0.75 | كم = 0.75 كم.
3. السرعة المتوسطة = إجمالي الإزاحة ÷ الوقت المنقضي:
v = − 0.75 km / 58 min = − 0.013 km/min
4. المسافة الإجمالية المقطوعة (مجموع مقادير النزوح الفردي) هي:
xTotal = Σ |Δxi| = 0.5 + 0.5 + 1.0 + 1.75 km = 3.75 km
5. يمكننا رسم بياني لموضع جيل مقابل الوقت كأداة مساعدة مفيدة لرؤية الحركة؛ يظهر الرسم البياني في الشكل 3.5 كما يلي:
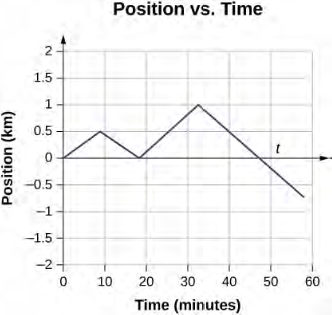
الشكل 3.5 يوضح هذا الرسم البياني موقف جيل مقابل الوقت. السرعة المتوسطة هي ميل الخط الذي يربط بين النقطتين الأولى والنهائية.
الدلالة
يبلغ إجمالي الإزاحة لجيل 0.75 كيلومترًا، مما يعني أنه في نهاية رحلتها ينتهي بها الأمر مسافة 0.75 كيلومتر غرب منزلها. يعني السرعة المتوسطة أنه إذا كان على شخص ما أن يمشي غربًا بسرعة 0.013 كم / دقيقة بدءًا من نفس الوقت الذي غادرت فيه جيل منزلها، فسيصل كلاهما إلى نقطة التوقف النهائية في نفس الوقت. لاحظ أنه إذا أنهت جيل رحلتها في منزلها، فسيكون إجمالي إزاحتها صفرًا، وكذلك سرعتها المتوسطة سوف تكون مساوية للصفر. المسافة الإجمالية المقطوعة خلال 58 دقيقة من الوقت المنقضي لرحلتها هي 3.75 كم.
تحقق من فهمك
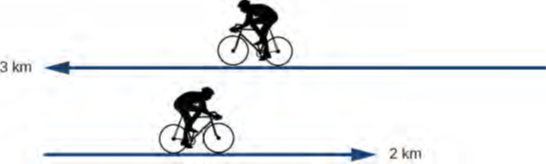
راكب دراجة يسير مسافة 3 كيلومترات غربًا ثم يستدير ويقود لمسافة 2 كيلومتر شرقًا. (أ) ما هي إزاحته؟ (ب) ما هي المسافة المقطوعة؟ (ج) ما هي القيمة المطلقة لإزاحته؟
المصدر
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.
