التسارع – متوسط التسارع والتسارع اللحظي
الأهداف: بنهاية هذا القسم حول موضوع التسارع – متوسط التسارع والتسارع اللحظي، سيكون القارئ قادرًا على:
- حساب متوسط التسارع بين نقطتين خلال فترة زمنية محددة.
- حساب التسارع اللحظي من دالة السرعة.
- شرح طبيعة متجه التسارع اللحظي ومتجه السرعة.
- شرح الفرق بين متوسط التسارع والتسارع اللحظي.
- إيجاد التسارع اللحظي في فترة زمنية محددة على الرسم البياني للسرعة مقابل الوقت.
المحتويات
تمتد أهمية فهم التسارع أو العَجَلة Acceleration إلى خبرتنا في الحياة اليومية، فضلاً عن الامتدادات الشاسعة للفضاء الخارجي والعالم الصغير للفيزياء دون الذرية. في المحادثة اليومية، التسريع يعني زيادة السرعة كما هي الحال عند الضغط على دواسة البنزين في السيارة؛ كما يؤدي الضغط على دواسة الفرامل إلى إبطاء السيارة. نحن على دراية بتسارع سيارتنا. كلما زاد التسارع أو العجلة، زاد التغيير في السرعة خلال فترة زمنية معينة. يُلاحظ التسارع على نطاق واسع في الفيزياء التجريبية. في تجارب معجل الجسيمات الخطي، على سبيل المثال، يتم تسريع الجسيمات دون الذرية إلى سرعات عالية جدًا في تجارب الاصطدام، والتي تخبرنا بمعلومات حول بنية العالم دون الذري وكذلك أصل الكون.
في الفضاء، الأشعة الكونية عبارة عن جسيمات دون ذرية تم تسريعها إلى طاقات عالية جدًا في السوبرنوفا (انفجار النجوم الضخمة) ونواة المجرة النشطة. من المهم أن نفهم العمليات التي تسرع الأشعة الكونية لأن هذه الأشعة تحتوي على إشعاع شديد الاختراق يمكن أن يلحق الضرر بالإلكترونيات المحمولة على المركبات الفضائية مثلاً.
متوسط التسارع
يتوافق التعريف الرسمي للتسارع مع هذه المفاهيم التي تم وصفها للتو، ولكنه أكثر شمولاً.
معادلة حساب متوسط التسارع
متوسط التسارع هو المعدل الذي تتغير فيه السرعة، ومن هذا التعريف يكون:
(3.8)
حيث a هي متوسط التسارع، وv هي السرعة، وt الزمن. (الخط تحت a يعني متوسط التسارع).
نظرًا لأن التسارع هو السرعة بالأمتار في الثانية مقسومًا على الوقت بالثواني، غالبًا ما يتم اختصار وحدات التسارع في النظام الدولي للوحدات متر / ث 2 – أي متر لكل ثانية تربيع أو متر لكل ثانية في الثانية. هذا يعني حرفيًا عدد الأمتار في الثانية التي تتغير فيها السرعة كل ثانية. تذكر أن السرعة متجه – لها المقدار والاتجاه – مما يعني أن التغيير في السرعة يمكن أن يكون تغيرًا في المقدار (أو السرعة)، ولكن يمكن أيضًا أن يكون تغيرًا في الاتجاه. على سبيل المثال، إذا تباطأ العداء الذي يجري بسرعة 10 كم/ساعة باتجاه الشرق إلى أن يتوقف، وعكس الاتجاه، واستمر في الجري بسرعة 10 كم / ساعة باتجاه الغرب، فقد تغيرت سرعته نتيجة للتغيير في الاتجاه، على الرغم من أن مقدار السرعة هي نفسها في كلا الاتجاهين. وهكذا، يحدث التسارع عندما تتغير السرعة في المقدار (زيادة أو نقصان السرعة) أو في الاتجاه، أو في كليهما.
التسارع ككمية متجهة
التسارع متجه يكون في نفس اتجاه التغير في السرعة Δv. نظرًا لأن السرعة متجه، فيمكن أن تتغير في المقدار أو في الاتجاه أو كليهما. وبالتالي، فإن التسارع هو تغيير في السرعة أو الاتجاه أو كليهما.
ضع في اعتبارك أنه على الرغم من أن التسارع يكون في اتجاه التغير في السرعة، إلا أنه لا يكون دائمًا في اتجاه الحركة. عندما يتباطأ جسم ما، فإن تسارعه يكون عكس اتجاه حركته. على الرغم من أن هذا يشار إليه عادةً باسم التباطؤ الشكل 3.10، إلا أننا نقول إن القطار يتسارع في اتجاه معاكس لاتجاه حركته.

الشكل 3.10: قطار مترو أنفاق في ساو باولو، البرازيل، يتباطأ عندما يصل إلى المحطة. إنه يتسارع في اتجاه معاكس لاتجاه حركته. (الصورة: بواسطة Yusuke Kawasaki)
يمكن لمصطلح التباطؤ أن يسبب ارتباكًا في تحليلنا لأنه ليس متجهًا ولا يشير إلى اتجاه معين فيما يتعلق بنظام إحداثيات، لذلك نحن لا نستخدمه. التسارع متجه (أو كمية متجهة)، لذلك يجب أن نختار الإشارة المناسبة له في نظام الإحداثيات الذي اخترناه. في حالة القطار في الشكل 3.10، يكون التسارع في الاتجاه السالب في نظام الإحداثيات المختار، لذلك نقول إن القطار يخضع لتسارع سلبي أو سالب.
إذا كانت سرعة الجسم المتحرك في الاتجاه الموجب بالنسبة إلى الأصل المختار واكتسب تسارعًا سلبيًا ثابتًا، فإن الجسم في النهاية يتوقف عن السير ويعكس اتجاهه. إذا انتظرنا لفترة كافية، يمر الجسم من خلال الأصل وهو يسير في الاتجاه المعاكس. هذا موضح في الشكل 3.11.
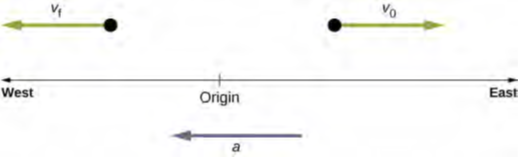
الشكل 3.11: جسم متحرك مع متجه سرعة باتجاه الشرق تحت تسارع سالب يتوقف عن الحركة ويعكس اتجاهه. يمر بالأصل في الاتجاه المعاكس بعد وقت طويل بما فيه الكفاية.
مثال 3.5: حساب متوسط التسارع
يتسارع حصان السباق الخارج من البوابة من السكون إلى ويصل إلى سرعة 15.0 م / ث باتجاه الغرب خلال 1.80 ثانية. ما هو متوسط تسارعه؟

إستراتيجية الحل
أولاً، نرسم مخططًا ونخصص نظام إحداثيات للمسألة، شكل 3.13. هذه مسألة بسيطة، لكنها تساعد دائمًا في رسمها. لاحظ أننا نصنف الشرق على أنه موجب والغرب سالب. وهكذا، في هذه الحالة، لدينا سرعة سالبة.
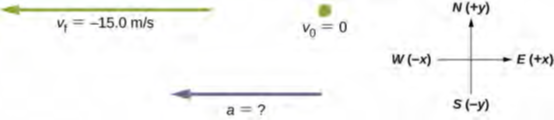
الشكل 3.13: حدد نظام الإحداثيات والمعلومات المقدمة كمعطيات وما تريد حسابه.
يمكننا حل هذه المسألة عن طريق تحديد Δv و t من المعلومات المعطاة، ثم حساب متوسط التسارع مباشرة من المعادلة:
الحل
أولاً، حدد العناصر المعروفة:v0 = 0 ، vf = −15.0 m/s (تشير الإشارة السالبة إلى الاتجاه نحو الغرب)، Δt = 1.80 s.
ثانيًا، أوجد التغير في السرعة. نظرًا لأن الحصان ينتقل من صفر إلى 15.0 م/ث، فإن التغير في السرعة يساوي سرعته النهائية:
Δv = vf – v0 = vf = −15.0 m/s
أخيرًا، استبدل القيم المعروفة (Δv و Δt) وحل من أجل المجهول a:
a = Δv / Δt = (−15.0 m/s) / (1.80 s) = −8.33 m/s2
الدلالة
تشير العلامة السالبة الخاصة بالتسارع إلى أن التسارع باتجاه الغرب. التسارع البالغ 8.33 م/ث2 باتجاه الغرب يعني أن الحصان يزيد سرعته بمقدار 8.33 م/ث باتجاه الغرب كل ثانية؛ أي 8.33 مترًا لكل ثانية في الثانية، ونكتبها على النحو التالي: 8.33 مترًا / ثانية2. هذا حقًا متوسط التسارع، لأن ركوب الخيل ليس سلسًا. نرى لاحقًا أن تسارعًا بهذا المقدار سيتطلب من الراكب التمسك بقوة تساوي وزنه تقريبًا.
تحقق من فهمك
يتم تسريع البروتونات في مسرع خطي من السكون إلى 2.0 × 10 7 م/ث في 10-4 ثوانٍ. ما هو متوسط تسارع البروتونات؟
التسارع اللحظي
يتم الحصول على التسارع اللحظي a، أو التسارع في لحظة زمنية محددة، باستخدام نفس العملية التي تمت مناقشتها من أجل إيجاد السرعة اللحظية. أي أننا نحسب متوسط التسارع بين نقطتين خلال فترة زمنية مفصولة بـ t ونترك Δt يقترب من الصفر. والنتيجة هي مشتق من دالة السرعة v(t)، وهي تسارع لحظي ويتم التعبير عنها رياضيًا على النحو التالي:
(3.9)
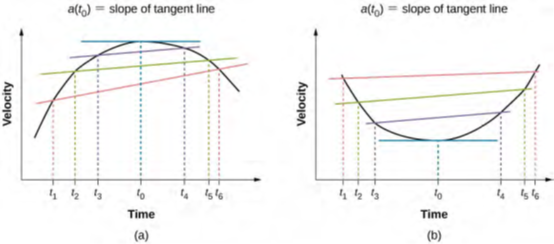
وهكذا، على غرار السرعة التي تكون مشتقًا من دالة الموضع، فإن التسارع اللحظي هو مشتق من دالة السرعة. يمكننا إظهار ذلك بيانيًا بنفس طريقة عرض السرعة اللحظية. في الشكل 3.14، التسارع اللحظي في الوقت t0 هو ميل الخط المماس للرسم البياني للسرعة مقابل الوقت في الوقت t0. نرى أن متوسط التسارع a = Δv / Δt يقترب من التسارع اللحظي عندما تقترب t من الصفر. أيضًا في الجزء (a) من الشكل، نرى أن السرعة لها حد أقصى عندما يكون ميلها صفرًا. هذا الوقت يتوافق مع الصفر في دالة التسارع. في الجزء (b)، يتم عرض التسارع اللحظي عند أدنى سرعة، والتي تكون أيضًا صفرًا ، نظرًا لأن ميل المنحنى يساوي صفرًا هناك أيضًا. وهكذا، بالنسبة لدالة سرعة معينة، تعطي أصفار دالة التسارع إما السرعة الدنيا أو القصوى.
مفهوم التسارع الثابت
الشكل 3.14: في رسم بياني للسرعة مقابل الوقت، التسارع اللحظي هو ميل خط المماس. (a) الموضح هو متوسط التسارع a = Δv/Δt = (vf – vi)/(tf – ti) بين الأوقات Δt = t6 – t1، Δt = t5 – t2، و t = t4 – t3. عندما Δt → 0 ، يقترب متوسط التسارع من التسارع اللحظي في الوقت t0. في العرض (a)، يتم عرض التسارع اللحظي للنقطة الموجودة على منحنى السرعة بأقصى سرعة. عند هذه النقطة، التسارع اللحظي هو ميل خط المماس، وهو صفر. في أي وقت آخر، لن يكون ميل خط المماس – وبالتالي التسارع اللحظي – صفرًا. (b) مثل (a) ولكن يعرض التسارع اللحظي بأدنى سرعة.
لتوضيح هذا المفهوم، دعونا نلقي نظرة على مثالين. أولاً، يتم عرض مثال بسيط باستخدام الشكل 3.9 (ب)، الرسم البياني للسرعة مقابل الوقت في المثال 3.3، لإيجاد التسارع بيانيًا. يوضح الشكل 3.15 (a) هذا الرسم البياني، وهو عبارة عن خط مستقيم. تم العثور على الرسم البياني المقابل للتسارع مقابل الوقت من منحنى السرعة ويظهر في الشكل 3.15 (b). في هذا المثال، دالة السرعة هي خط مستقيم بميل ثابت، وبالتالي فإن التسارع ثابت.
في المثال التالي، دالة السرعة لها اعتماد وظيفي أكثر تعقيدًا على الوقت.
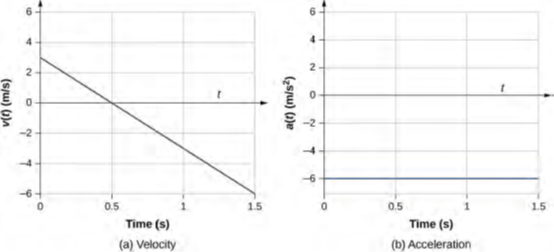
الشكل 3.15 (a, b): الرسم البياني للسرعة مقابل الوقت هو رسم خطي وله ميل ثابت سالب (شكل a) أو يساوي التسارع، كما هو موضح في (شكل b).
إذا عرفنا الشكل الوظيفي أو دالة السرعة، v(t)، فيمكننا حساب التسارع أو العجلة اللحظية a(t) في أي نقطة زمنية أثناء الحركة باستخدام المعادلة 3.9.
مثال 3.6: حساب التسارع اللحظي
الجسيم يتحرك ويتسارع. دالة السرعة هي:
أ. أوجد دالة التسارع (أو العجلة).
ب. أوجد السرعة اللحظية عند t = 1 و 2 و 3 و 5 ثانية.
ج. أوجد التسارع اللحظي عند t = 1 و 2 و 3 و 5 ثانية.
د. فسر نتائج (ج) من حيث اتجاهات متجهات التسارع والسرعة.
إستراتيجية الحل
نوجد صيغة دالة التسارع بأخذ المشتقة الأولى لدالة السرعة. ثم نحسب قيم السرعة اللحظية والتسارع من الدوال المعينة لكل منهما. بالنسبة للجزء (د)، نحتاج إلى مقارنة اتجاهات السرعة والتسارع في كل مرة.
الحل
أ.
a(t) = dv(t)/dt = 20 – 10 t m/s2
ب.
v(1s) = 15 m/s , v(2s) = 20 m/s , v(3s) = 15 m/s , v(5s) = −25 m/s
ج.
a(1s) = 10 m/s2 , a(2s) = 0 m/s2 , a(3s) = −10 m/s2 , a(5s) = −30 m/s2
د.
عند t = 1 s، تكون السرعة v (1s) = 15 m/s موجبة والتسارع موجب، لذا فإن كلا من السرعة والتسارع في نفس الاتجاه. يتحرك الجسيم بشكل أسرع.
عند t = 2 s، زادت السرعة إلى v (2s) = 20 m/s، حيث تكون الحد الأقصى، والذي يتوافق مع الوقت الذي يكون فيه التسارع صفرًا. نلاحظ أن السرعة القصوى تحدث عندما يكون ميل دالة السرعة صفرًا، وهو ما يمثل صفرًا لدالة التسارع.
عند t = 3 s، تكون السرعة v (3s) = 15 m/s والتسارع سالب. الجسيم قد قلل من سرعته ومتجه التسارع سالب. الجسيم يتباطأ.
عند t = 5 s، تكون السرعة v (5s) = −25 m/s ويكون التسارع سالبًا بشكل متزايد. بين الأوقات t = 3 s و t = 5 s، انخفضت سرعة الجسيم إلى الصفر ثم أصبحت سالبة، وبالتالي عكس اتجاهه. الجسيم يتسارع الآن مرة أخرى، لكن في الاتجاه المعاكس.
يمكننا رؤية هذه النتائج بيانياً في الشكل 3.16.
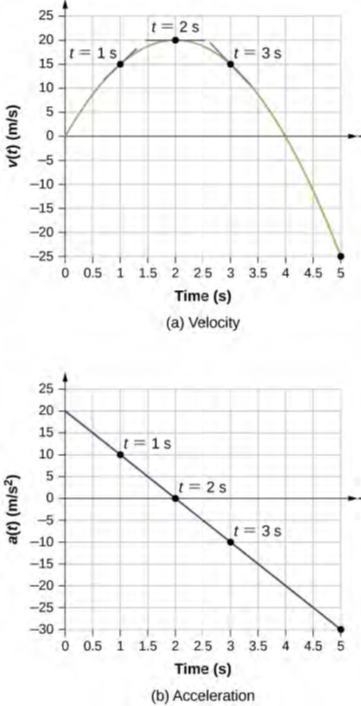
الشكل 3.16 (a) السرعة مقابل الوقت. يشار إلى خطوط الظل في الأوقات 1 و 2 و 3 s. منحنيات خطوط الظل هي التسارع. عند t = 3 s، تكون السرعة موجبة. عند t = 5 s، تكون السرعة سالبة، مما يدل على عكس اتجاه حركة الجسيم. (b) التسارع مقابل الوقت. بمقارنة قيم التسارع التي قدمتها النقاط السوداء مع المنحنيات المقابلة لخطوط الظل (منحنيات الخطوط عبر النقاط السوداء) في (a)، نرى أنها متطابقة.
الدلالة
من خلال القيام بتحليل عددي وتحليل بياني لسرعة الجسيم وتسارعه، يمكننا معرفة الكثير عن حركته. يكمل التحليل العددي التحليل البياني في إعطاء نظرة شاملة للحركة. يتوافق صفر دالة التسارع مع أقصى سرعة في هذا المثال.
في هذا المثال أيضًا، عندما يكون التسارع موجبًا وفي نفس اتجاه السرعة، تزداد السرعة. عندما يميل التسارع نحو الصفر، يصبح في النهاية سالبًا، تصل السرعة إلى الحد الأقصى، وبعد ذلك تبدأ في التناقص. إذا انتظرنا فترة طويلة بما فيه الكفاية، تصبح السرعة أيضًا سالبة، مما يشير إلى انعكاس الاتجاه. من الأمثلة الواقعية على هذا النوع من الحركة سيارة ذات سرعة تتزايد إلى أقصى حد، وبعد ذلك تبدأ في التباطؤ، وتتوقف، ثم ينعكس اتجاه حركتها.
تحقق من فهمك
طائرة تهبط على مدرج متجه شرقا. صف تسارعها.
الشعور بالتسارع
ربما تكون معتادًا على تجربة التسارع عند الصعود إلى المصعد أو الضغط على دواسة الوقود في سيارتك.
ومع ذلك، فإن التسارع يحدث للعديد من الأشياء الأخرى في كوننا والتي ليس لدينا اتصال مباشر معها. يعرض الجدول 3.2 تسارع الكائنات المختلفة. يمكننا أن نرى مقادير التسارع تمتد على عدة مستويات من حيث المقدار.
| التسارع | قيمة التسارع (m/s2) |
| قطار فائق السرعة | 0.25 |
| المصعد | 2 |
| الفهد | 5 |
| جسم في حالة سقوط حر بدون مقاومة للهواء بالقرب من سطح الأرض | 9.8 |
| الحد الأقصى لمكوك الفضاء أثناء الإطلاق | 29 |
| ذروة المظلة أثناء الفتح العادي للمظلة | 59 |
| طائرة أف 16 تنسحب من الغارة | 79 |
| قذف مقعد متفجر من الطائرة | 147 |
| صاروخ سبرينت | 982 |
| ذروة تسارع أسرع مزلقة صاروخية | 1.540 |
| قفز البراغيث | 3.200 |
| ضرب البيسبول بمضرب | 30.000 |
| إغلاق فك النملة الفكية | 1000.000 |
| البروتون في مصادم الهادرون الكبير | 1.9 × 10 9 |
الجدول 3.2 القيم النموذجية للتسارع (الصورة: ويكيبيديا، مستويات التسارع)
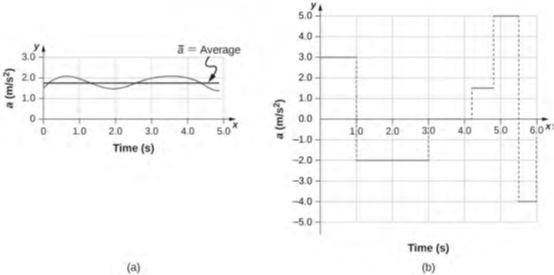
في هذا الجدول، نرى أن التسارعات النموذجية تختلف اختلافًا كبيرًا باختلاف الأجسام وليس لها علاقة بحجم الجسم أو مقدار كتلته. يمكن أن يختلف التسارع أيضًا بشكل كبير مع مرور الوقت أثناء حركة الجسم. متسابق سباق السيارات لديه تسارع كبير بعد بداية السباق مباشرة، لكنه يتضاءل بعد ذلك عندما تصل السيارة إلى سرعة ثابتة. يمكن أن يكون متوسط تسارعه مختلفًا تمامًا عن تسارعه اللحظي في وقت معين أثناء حركته. يقارن الشكل 3.17 متوسط التسارع بيانيًا مع التسارع اللحظي لحركتين مختلفتين للغاية.
الدلالة
الشكل 3.17: رسوم بيانية للتسارع اللحظي مقابل الوقت لحركتين مختلفتين أحادية البعد. (a) يختلف التسارع بشكل طفيف ودائمًا ما يكون في نفس الاتجاه لأنه إيجابي. المتوسط خلال الفترة الزمنية هو تقريبًا نفس التسارع في أي لحظة. (b) يختلف التسارع اختلافًا كبيرًا، ربما يمثل حزمة على حزام ناقل لمكتب البريد يتم تسريعها للأمام والخلف أثناء ارتطامها. من الضروري مراعاة فترات زمنية صغيرة (مثل من صفر إلى 1.0 ثانية) مع تسارع ثابت أو شبه ثابت في مثل هذه الحالة.
المصدر
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.