ملخص المحتوى
التحليل الإحصائي للبيانات وأهميته وخطواته، التوزيع التكراري، مقاييس النزعة المركزية (الوسط أو المتوسط الحسابي والوسيط والمنوال)، مقاييس التشتت، التوزيع، معامل الارتباط، الانحدار.
المحتويات
مفهوم التحليل الإحصائي للبيانات
من أجل إنجاح مرحلة تحضير البيانات للتحليل واللتنقيب ومن ثم إنجاح عمليات تنقيب البيانات نفسها وسائر إجراءات البحث العلمي بكافة أشكاله وبكل أنواعه، فإنه من الضروري أن يكون لدينا صورة وصفية عامة للبيانات التي يتم التخطيط لتحليلها أو للتنقيب فيها.
ويتم ذلك من خلال التحليل الإحصائي الوصفي لهذه البيانات (بالإنجليزية: Statistical Data Analysis).
ويمكن الحصول على الصورة الوصفية باستخدام المبادئ الأساسية للإحصاء الوصفي والأدوات المختلفة التي توفرها من أجل التحليل الإحصائي للبيانات ووصفها من منظور إحصائي، وذلك من أجل التعرف على سمات أو خصائص البيانات وإلقاء الضوء عليها عن قرب.
أهمية التحليل الإحصائي للبيانات
تكمن أهمية التحليل الإحصائي للبيانات في أنه يوفر وصفًا أوليًا للبيانات محل البحث أو الدراسة، بحيث يساعد الباحث أو المحلل على فهم طبيعة البيانات قبل البدء بإجراءات أخرى من إجراءات البحث العلمي وتنقيب البيانات، كاختبار الفرضية كما في البحث العلمي، أو تطبيق الخوارزميات كما في حالة التنقيب في قواعد البيانات.
خطوات التحليل الإحصائي للبيانات
تشتمل خطوات التحليل الإحصائي للبيانات على مجموعة من المقاييس الإحصائية المتنوعة. ومنها التوزيع التكراري أو (بالإنجليزية: Frequency Distribution). ومقاييس النزعة المركزية أو (بالإنجليزية: Central Tendency) التي تحدد طريقة توزيع البيانات حول المركز، وتشتمل على المتوسط الحسابي والوسيط والمنوال. كما تشتمل على مقاييس التشتت (بالإنجليزية: Dispersion)، والمدى، والمدى الربعي، والتباين والانحراف المعياري. وكذلك مقاييس الارتباط أو (بالإنجليزية: Correlation) والانحدار (بالإنجليزية: Regression). هذا بالإضافة لبعض أساليب الوصف و التحليل الإحصائي للبيانات باستخدام الأشكال البيانية أو (بالإنجليزية: Graphics)، التمثيل البياني بالأعمدة والقطاعات الدائرية والرسوم الخطية والهندسية المتنوعة.

وفيما يلي شرحًا مفصلاً لكل المقاييس الإحصائية:
التوزيع التكراري
مفهوم التوزيع التكراري في التحليل الإحصائي للبيانات
لكل مجموعة من القيم المعروضة بصورة عشوائية لا يمكن وصفها إحصائيًا بسهولة، وقد لا نتمكن من شرحها أو تفسيرها بوضوح. ولهذا نلجأ إلى مقياس التوزيع التكراري (بالإنجليزية: Frequency Distribution)، وهو عملية يتم فيها تبويب البيانات في جداول تكرارية أو عرضها برسومات بيانية على شكل أعمدة أو مدرج أو مضلع تكراري بحسب طبيعة البيانات الإحصائية.
فإذا جاءت علامات مجموعة من الأفراد في اختبار تحصيلي، بعد أن تعلموا بطريقة معينة، بصورتها الأولية كما هي في التوزيع الافتراضي التالي:
| 19 | 26 | 21 | 20 | 19 | 21 |
| 20 | 22 | 18 | 20 | 20 | 23 |
| 21 | 20 | 22 | 20 | 19 | 20 |
| 24 | 22 | 19 | 19 | 21 |
فإن جميع هذه القيم بالنسبة للمتغير مدار البحث مجموعة كلية أو فئة واحدة.
إلا أنه يمكن تقسيم هذه الفئة إلى عدة فئات أو مجموعات جزئية بحيث:
- تنتمي كل قيمة لفئة واحدة.
- تتساوى طول الفئات لتسهيل الإجراءات أو العمليات الإحصائية.
- تبقى الفئات متصلة، أي لا يوجد إهمال للفئات التي تكرارها صفر.
- تستنفذ الفئات جميع القيم حتى لو كانت القيم متطرفة.
- يكون عدد الفئات مناسبًا لمدى القيم، أي يكون هناك توازن بين سهولة عرض وتفسير البيانات.
طول الفئة في الجدول التكراري
إن طول الفئة في الجدول التكراري يعتمد على مدى القيم وعدد الفئات التي يقترحها الباحث.
في البيانات السابقة مثلا لا يُحتمل أن يتم تقسيمها بطول فئة أكبر من واحد. حيث يوفر هذا الطول عددًا مناسبًا من الفئات كما في الجدول التالي. حيث يستحسن ألا تقل عن خمس فئات ولا تزيد عن 15 فئة.
بناء جدول التوزيع التكراري في التحليل الإحصائي
| التكرار (ت) | مركز الفئة (س) |
| 1 | 26 |
| 0 | 25 |
| 1 | 24 |
| 1 | 23 |
| 3 | 22 |
| 4 | 21 |
| 7 | 20 |
| 5 | 19 |
| 1 | 18 |
المضلع التكراري في التحليل الإحصائي للبيانات
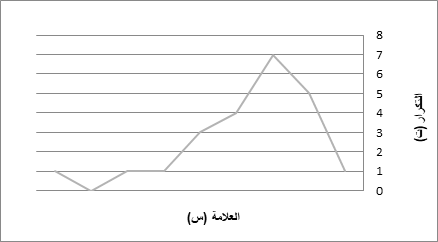
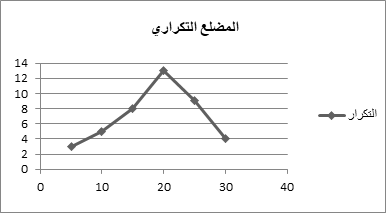
الخطوة التي يسهّل فيها الباحث عرض البيانات الإحصائية بعد وضعها في جدول تكراري هي وضعها بصورة مضلع تكراري. ويوفر المضلع التكراري إعطاء فكرة سريعة عن طبيعة البيانات وتوزيعها من حيث التفلطح (بالإنجليزية: Kurtosis) والالتواء أو (بالإنجليزية: Skewness).
يبين الشكل التالي عرضًا بيانيًا للتوزيع التكراري في الجدول السابق بصورة مضلع تكراري. حيث يفترض دائمًا أن توزيع القيم في الفئة توزيعًا منتظمًا وأن مركز الفئة هو المتوسط أو الوسط الحسابي للقيم في تلك الفئة:
التمثيل البياني بالأعمدة والقطاعات الدائرية
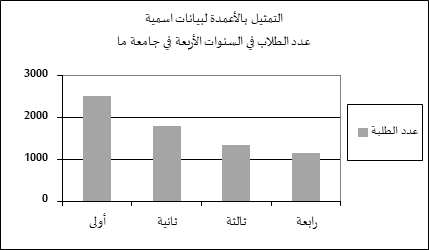
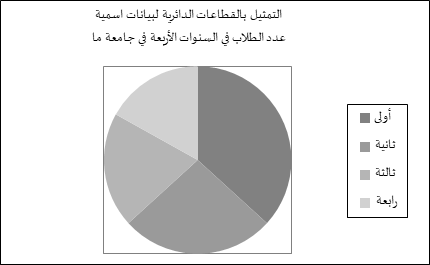
إذا كانت البيانات واقعة على متغير اسمي (تصنيفي) فلا تمثل بمضلع تكراري وإنما تمثل التكرارات أو نسبة التكرارات الواقعة ضمن كل فئة من فئات المتغير إما بالأعمدة (حيث يمثل ارتفاع العمود التكرار أو النسبة).
ويحدد موقع العمود بطريقة منطقية على الخط الأفقي أو الرأسي كما هو مبين في الشكل التالي، أو بالقطاعات الدائرية كما هو مبين في الشكل الذي يليه، والذي يشير إلى نسبة الطلبة في السنوات الجامعية الأربعة في جامعة ما (حيث تمثل النسبة بمساحة القطاع في الدائرة).
مقاييس النزعة المركزية
من أدوات الوصف و التحليل الإحصائي للبيانات مقاييس النزعة المركزية أو (بالإنجليزية: Central Tendency). ومقاييس النزعة المركزية تخبرنا بطريقة توزيع البيانات وأكثرية القيم فيها. ومن أهم المقاييس وأكثرها انتشارًا هو الوسط أو المتوسط الحسابي الذي يحدد مركز مجموعة من البيانات بطريقة حسابية.
1. المتوسط الحسابي
المتوسط الحسابي أو الوسط الحسابي (بالإنجليزية: Mean) لمجموعة من القيم هو حاصل قسة مجموع هذه القيم على عددها.
أي أن:
المتوسط الحسابي لمجموعة من القيم = مجموع القيم ÷ عددها
فإذا كان لدينا بيانات رواتب مجموعة من الموظفين في إحدى الشركات، وكانت رواتبهم معرفة من خلال الفئة (س) التي تضم رواتب عدد (ن) من الموظفين كما يلي:
س = (س1، س2، س3، س4، …. ، سن)
فيكون المتوسط الحسابي لرواتب كل الموظفين هو:
المتوسط الحسابي = (س1 + س2 + س3 + س4 +.. + س ن) ÷ ن
مثلا، إذا كانت لدينا هذه القيم للرواتب السنوية (بالآلاف) لمجموعة من الموظفين مرتبة تصاعديًا كما يلي:
30، 36، 47، 50، 52، 52، 56، 60، 63، 70، 70، 110
فباستخدام تعريف المتوسط الحسابي يكون:
المتوسط الحسابي = (30 + 36 + 47 + 50 + 52 + 52 + 56 + 60 + 63 + 70 + 70 + 110) ÷ 12 = 58
أي أن متوسط الرواتب لكل الموظفين هو 58000.
مشكلات المتوسط الحسابي في التحليل الإحصائي للبيانات
بالرغم من كثرة استخدام المتوسط الحسابي باعتباره كمية تساعد في التحليل الإحصائي للبيانات ووصفها إلاّ أنها لا تُعتبر الطريقة المثلى لقياس مركز البيانات.
والمشكلة الأساسية في المتوسط الحسابي أو الوسط الحسابي كأحد مقاييس النزعة المركزية هو أنه يتأثر بالقيم المتطرفة من مجموعة القيم الموجودة ضمن البيانات.
ويُقصد بـ القيم المتطرفة هي تلك القيم الكبيرة نسبيًا أو الصغيرة نسبيًا مقارنة مع بقية القيم، حيث يمكن أن يؤثر عدد قليل من مثل تلك القيم على قيمة المتوسط الحسابي الذي يتم احتسابه.
مثال توضيحي لتأثر المتوسط الحسابي بالقيم المتطرفة
في إحدى الشركات قد يتأثر متوسط الرواتب ويرتفع نتيجة لوجود عدد قليل من المدراء من ذوي الرواتب العالية نسبيًا. وبنفس الطريقة يمكن أن يتأثر متوسط درجات طلاب أحد الصفوف في أحد الامتحانات سلبًا نتيجة لوجود قيم أو درجات متدنية جدًا لبعض الطلاب.
ولإيقاف هذا التأثير الذي يتسبب به بعض القيم المتطرفة، العالية جدًا أو المنخفضة جدًا، يمكن استخدام طريقة المتوسط الحسابي المقلّم أو المقلّص (بالإنجليزية: Trimmed Mean). والمتوسط الحسابي المقلّم أو المقلّص هو الذي يتم الحصول عليه بعد اقتطاع القيم المتطرفة العُليا والدنيا من مجموعة البيانات.
ففي المثال السابق، يتم استثناء عدد من القيم مثل الأولى والأخيرة (30، 110) باعتبارها قيم متطرفة ومن ثم يتم احتساب المتوسط الحسابي لبقية البيانات.
وبالرغم من إمكان تطبيق هذه الطريقة بسهولة إلاّ أنه ينبغي تجنب حذف عدد كبير من القيم المتطرفة من الاتجاهين لكي لا يؤدي ذلك إلى فقدان قيمة ودلالة البيانات.
حساب المتوسط الحسابي من الجدول التكراري
أما إذا كانت البيانات مبوبة في جدول تكراري فإن المتوسط يمكن حسابه باستخدام المعادلة التالية:
المتوسط الحسابي للبيانات المبوبة في جدول تكراري = مجموع حاصل ضرب (مركز الفئة × تكرار الفئة) ÷ حجم العينة
مثلا في التوزيع التكراري التالي:
| الفئة | مركز الفئة | التكرار |
| 15 – 17 | 16 | 1 |
| 12 – 14 | 13 | 2 |
| 9 – 11 | 10 | 3 |
| 6 – 8 | 7 | 3 |
| 3 – 5 | 4 | 1 |
بتطبيق معادلة حساب المتوسط الحسابي:
المتوسط الحسابي = (1 × 16 + 2 × 13 + 3 × 10 + 3 × 7 + 1 × 4) ÷ 10
المتوسط الحسابي = 9.7
يُشكل الوسط أو المتوسط الحسابي نقطة الاتزان لأي توزيع. بمعنى أن مجموع انحرافات العلامات عن المتوسط = صفر.
ومن الخصائص الأخرى للوسط أنه الأقل تأثرًا بتقلبات العينة. ولذلك فهو مقياس النزعة المفضل في مجال الإحصاء الاستدلالي.
2. الوسيط
الوسيط أو (بالإنجليزية: Median) هو من مقاييس النزعة المركزية ويُعبر بشكل أدق عن مركز البيانات لأنه القيمة التي تقع في منتصف مجموعة من القيم المرتبة. والوسيط هو القيمة التي تقسم البيانات إلى جزئين بحيث يقع الجزء الأول قبله والجزء الثاني بعده في الترتيب.
وفي مجال الإحصاء والاحتمالات فإن الوسيط يطبق بشكل عام على البيانات الرقمية بالإضافة للبيانات من النوع الرتبي.
ولأي عدد (ن) من القيم لأحد المتغيرات (س) المرتبة ترتيبًا تصاعديًا يكون الوسيط هو القيمة التي توجد في منتصف هذا الترتيب إذا كانت (ن) عدد فردي.
أي أن:
الوسيط لعدد فردي ن من القيم = القيمة رقم (ن + 1) ÷ 2
أما إذا كانت (ن) عدد زوجي فإن الوسيط يكون القيمتين اللتين تقعان في المنتصف.
أي أن:
الوسيط لعدد زوجي ن من القيم هو القيمتين ذوات الترتيب (ن/2) و (ن/2)+1
وإذا كانت البيانات من النوع الرقمي يكون الوسيط هو المتوسط الحسابي للقيمتين.
لقراءة المزيد حول البيانات من النوع الرتبي أو من البيانات من النوع الرقمي يمكن مراجعة موضوع أنواع البيانات وخصائصها.
مثال توضيحي لمقياس الوسيط في التحليل الإحصائي
في المثال السابق، لو كانت هذه هي قيم رواتب مجموعة الموظفين:
30، 36، 47، 50، 52، 52، 56، 60، 63، 70، 70، 110
فطالما أن عدد القيم هو عدد زوجي (12) قيمة، فإن الوسيط في هذه الحالة يكون ممثلا بالقيمتين السادسة والسابعة، وهما القيمتين (52، 56).
وبالتالي تكون قيمة الوسيط هي المتوسط الحسابي لهاتين القيمتين كما يلي:
الوسيط = (52 + 56) ÷ 2 = 54
أما لو قمنا بحذف القيمة الأخيرة فقط واعتبرنا أن البيانات هي:
30، 36، 47، 50، 52، 52، 56، 60، 63، 70، 70
فيكون عدد القيم في هذه الحالة هو (11) قيمة.
وبالتالي يكون الوسيط هو العدد ذو الترتيب = (11+1) ÷ 2 = 6
أي أن الوسيط هو القيمة السادسة في الترتيب وهي القيمة 52.
الوسيط و المئين
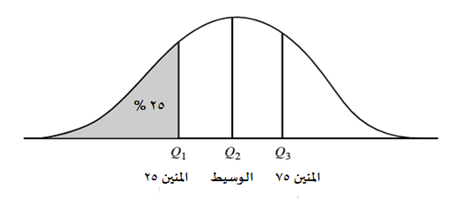
يُعرف الوسيط أيضًا بأنه “المئين 50″، وبنفس الطريقة يمكن تعريف ما يُسمى بالقيم المئينية، على أنها القيم التي تقسم البيانات إلى قسمين بالنسبة المئوية المذكورة. مثلا المئين 25 (بالإنجليزية: 25th Percentile) هو القيمة التي تقسم مجموعة من البيانات إلى قسمين بنسبة 25% منها تقع تحت تلك القيمة و75% منها تقع فوقها.
الشكل التالي هو رسم بياني يوضح الوسيط والمئين 25 والمئين 75:
3. المنوال
يمكن إعطاء وصفًا كميًا سريعًا للبيانات بعد تبويبها بالنظر إلى القيمة المنوالية. ويُعرف المنوال (بالإنجليزية: Mode) بأنه القيمة أو مركز الفئة أو الصفة المقابلة لأعلى تكرار في البيانات. والمنوال هو أبسط مقاييس النزعة المركزية من حيث إمكانية إيجاد قيمته، إلا أنه محدود الاستعمال. فهو أداة التحليل الإحصائي للبيانات الوحيدة التي يمكن استخدامها عندما تكون البيانات بمستوى القياس التصنيفي أو الاسمي.
ويتأثر المنوال كثيرًا بحجم العينة، وبتغير طول فئة البيانات ولذلك يعتبر قليل الثبات. كما أن المنوال لا يدخل كثيرًا في تحليلات إحصائية متقدمة في التحليل الإحصائي للبيانات.
ففي المثال الخاص برواتب مجموعة من الموظفين، الممثلة بالقيم التالية:
30، 36، 47، 50، 52، 52، 56، 60، 63، 70، 70، 110
يكون المنوال = 52
أما في حالة التوزيع التكراري للفئات، فإذا كان في التوزيع فئتين متتاليتين أو أكثر وكانت متساوية في التكرار وبنفس الوقت أعلى التكرارات فإن المنوال هو معدل مراكز هاتين الفئتين.
مثال توضيحي لاستخدام المنوال في التحليل الإحصائي
التوزيع التكراري التالي ثنائي المنوال وهما القيمتين: 22، 12
| الفئة | التكرار |
| 30 – 34 | 1 |
| 25 – 29 | 3 |
| 20 – 24 | 8 |
| 15 – 19 | 4 |
| 10 – 14 | 8 |
| 5 – 9 | 2 |
وُيلاحظ أنه يمكن أن تتشابه مجموعتين من البيانات وتتطابق قيم كل من الوسط أو المتوسط الحسابي والوسيط لهما. ومع ذلك يكون هناك اختلاف في طبيعة قيم كل مجموعة من حيث قربها أو بعدها عن المتوسط الحسابي أو الوسيط، فمثلا المجموعتين التاليتين من القيم:
10، 20، 30، 40، 50، 60
0، 10، 15، 55، 60، 70
لهما نفس المتوسط الحسابي وهو 35، ولكن البيانات في المجموعة الأولى تختلف عنها في المجموعة الثانية من حيث القيم من جهة ومن حيث البُعد عن المتوسط الحسابي من جهة أخرى. ومن هذا المنطلق ظهرت مقاييس إحصائية أخرى تختص بقياس مدى تشتت البيانات وبُعدها عن مقاييس النزعة المركزية.
التحليل الإحصائي للبيانات باستخدام مقاييس التشتت
مما سبق يتضح أنه لن يكون التحليل الإحصائي للبيانات أو وصفها كاملا بتحديد شكلها أو بتحديد مقياس النزعة المركزية الذي يناسبها وإنما قد يكتمل بتحديد درجة انتشار القيم المختلفة باستخدام مقياس مناسب من مقاييس التشتت (بالإنجليزية: Dispersion). وفيما يلي تفصيلا لثلاثة مقاييس تشتت وهي المدى، التباين والانحراف المعياري.
1. المدى
المدى (بالإنجليزية: Range) يمثل المسافة بين أكبر قيمة وأقل قيمة في مجموعة البيانات، والذي يُعتبر من أبسط مقاييس التشتت.
أي أن:
المدى لمجموعة من القيم = أكبر قيمة – أصغر قيمة
ففي المثال السابق، لو كانت هذه هي قيم رواتب مجموعة الموظفين:
30، 36، 47، 50، 52، 52، 56، 60، 63، 70، 70، 110
يكون:
المدى = 110 – 30 = 80
كما يوجد نوعين آخرين للمدى وهما:
أ- المدى الربيعي
المدى الربيعي من مقاييس التشتت، وهو الفرق بين قيمتي المئين 75 والمئين 25. وعادة ما يُستخدم المدى الربيعي كمقياس تشتت عندما يُستخدم الوسيط كإحصائي نزعة مركزية. أي عندما تكون البيانات واقعة على مقياس رتبي أو عندما يكون في البيانات قيم متطرفة أو فئات مفتوحة.
ويمكن حساب المدى الربيعي بنفس طريقة حساب الوسيط مع استبدال القيمة 50 بالقيم 25 و75 في المعادلة الخاصة بحساب الوسيط.
ب- المدى العشيري
وهو الفرق بين قيمتي المئين 90 والمئين 10. والملاحظ أن الفرق بين المدى العشيري والمدى الربيعي يكمن في النسبة المئوية للحالات المستبعدة في ذيلي التوزيع. ولذلك يُعتبر المدى العشيري بديلا للمدى الربيعي إذا لوحظ بأن نسبة القيم التي تم اقتطاعها عالية نسبيًا.
ويمكن حساب المدى العشيري بنفس طريقة حساب الوسيط مع استبدال القيمة 50 بالقيم 10 و90 في المعادلة الخاصة بحساب الوسيط.
وتنبع أهمية الحديث عن المدى الربيعي أو المدى العشيري كأحد مقاييس التشتت من ضرورة الانتباه إلى القيم المتطرفة وأثرها على النتائج وعلاقتها بحجم البيانات ومعالجتها بالطريقة المناسبة.
2. التباين
التباين (بالإنجليزية: Variance) من مقاييس التشتت وهو معدل مربعات انحرافات القيم الواردة في البيانات عن الوسط أو المتوسط الحسابي.
ويُرمز إلى التباين بالرمز σ2 (ويُقرأ سيجما تربيع)، وهو يوضح مدى تشتت النواتج المحتملة عن قيمة المتوسط الحسابي (س).
معادلة حساب التباين
التباين = مجموع (س ن – س)2 ÷ ن
مثال على حساب التباين
نفرض أنه لدينا مجموعة من القيم التي نريد إيجاد قيمة الانحراف المعياري لها، والقيم هي كما يلي:
5، 7، 8، 10، 20
أولا: بتطبيق معادلة حساب الوسط أو المتوسط الحسابي، يكون لدينا:
المتوسط الحسابي = (5 + 7 + 8 + 10 + 20) ÷ 5
أو:
المتوسط الحسابي = 8
ثانيًا: بتطبيق معادلة حساب التباين، حيث لدينا:
التباين = مجموع (س ن – س)2 ÷ ن
أي أن:
التباين = ((س 1 – س)2 + (س 2 – س)2 + (س 3 – س)2 + (س 4 – س)2 + (س 5 – س)2) ÷ ن
والآن بالتعويض عن القيم الخمسة وقيمة الوسط أو المتوسط الحسابي، نحصل على:
التباين = ((5 – 8)2 + (7 – 8)2 + (8 – 8)2 + (10 – 8)2 + (20 – 8)2) ÷ 5
التباين = (9 + 1 + 0 + 4 + 144) ÷ 5
أي أن:
التباين = (158) ÷ 5 = 31.6
3. الانحراف المعياري
الانحراف المعياري أو (بالإنجليزية: St. Deviation) هو من مقاييس التشتت، وهو يساوي الجذر التربيعي للتباين. ويتضح أن التباين والانحراف المعياري يعتمدان في قيمتيهما على الوسط أو المتوسط الحسابي.
معادلة حساب الانحراف المعياري:
الانحراف المعياري = الجذر التربيعي للتباين
أو:
الانحراف المعياري = الجذر التربيعي لـ (مجموع (س ن – س)2 ÷ ن)
مثال على حساب الانحراف المعياري
في المثال السابق لحساب التباين، توصلنا إلى أن:
التباين = 31.6
بأخذ الجذر التربيعي للطرفين:
الجذر التربيعي للتباين = الجذر التربيعي لـ (31.6)
أو:
الانحراف المعياري = 5.62
التحليل الإحصائي للبيانات باستخدام التوزيع
عند وضع البيانات في صورة مضلع تكراري فإنه يوفر إعطاء فكرة سريعة عن طبيعة توزيع أو (بالإنجليزية: Distribution) البيانات من حيث التفلطح والالتواء.
1. خاصية الالتواء
تُشير خاصية الالتواء أو (بالإنجليزية: Skewness) إلى درجة ابتعاد المنحنى التكراري عن التماثل. فقد تكون معظم القيم في الطرف الأدنى من التوزيع ويقل تكرار القيم كلما اقتربنا من الطرف الأعلى. وفي هذه الحالة يُوصف توزيع البيانات بأنه ملتوي التواء موجب. أما إذا كان العكس فيوصف بأنه ملتوي التواء سالب.
2. خاصية التفلطح
تُشير خاصية التفلطح أو (بالإنجليزية: Kurtosis) إلى درجة تركيز التكرارات في منطقة الوسط للبيانات بالنسبة للتركيز في الطرفيين مقارنة بالتوزيع الطبيعي القياسي.
الشكل التالي يوضح التفلطح والالتواء في المضلع التكراري:
التحليل الإحصائي للبيانات باستخدام معاملات الارتباط
من أساليب التحليل الإحصائي للبيانات ما يسمى بمعاملات الارتباط. ومعامل الارتباط (بالإنجليزية: Coefficient Correlation) هو مفهوم إحصائي يوضح العلاقة بين متغيرين أو أكثر. ونظرًا لتعدد أنواع البيانات أو المتغيرات فقد تعددت أنواع معاملات الارتباط وطرق حسابها.
والهدف من استخدام معاملات الارتباط المختلفة يكون لإيجاد العلاقة بين متغيرين، وهل هي علاقة إيجابية أو سلبية، قوية أو ضعيفة. كما تأتي أهمية دراسة الارتباط من دوره في التنبؤ كطريقة من طرق الحصول على المعرفة. فإذا كان الارتباط قويًا بين متغيرين فهذا يعني إمكانية تقدير قيمة أحد المتغيرين عند معرفة القيمة المقابلة للمتغير الآخر بدقة أكبر مما لو كان الارتباط ضعيفًا.
الارتباط البسيط
يُقصد بالارتباط البسيط العلاقة بين متغيرين بصرف النظر عن نوع أي منهم من حيث نوع القياس ، وأكثرها شيوعًا هو الارتباط بين متغيرين كل منهما على المقياس الفئوي أو مقياس النسبة. ويحدد الارتباط عادة بالقوة والاتجاه.
وتتلخص إجراءات التحليل الإحصائي للبيانات باستخدام معاملات الارتباط في الكشف عن شدة أو قوة علاقة الارتباط واتجاهها من خلال كل من:
- رسم شكل الانتشار
- حساب معامل الارتباط
- دلالة معامل الارتباط في التحليل الإحصائي
وقد تم تناول معامل الارتباط بشيء من التفصيل في الفصل التالي من موسوعة البحث العلمي وهو بعنوان: معاملات الارتباط وأنواعها وطرق حسابها، ويمكن قراءة هذا الموضوع من خلال الدخول إلى الرابط التالي: معامل الارتباط – مفهومه ودلالته وأنواعه المختلفة.
التحليل الإحصائي للبيانات باستخدام تحليل الانحدار
تحليل الانحدار أو (بالإنجليزية: Regression) هو أسلوب يمكن بواسطته تقدير قيمة أحد متغيرين بمعلومية قيمة متغير آخر عن طريق معادلة رياضية تُسمى معادلة الانحدار وهي المعادلة التي تربط المتغيرين مع بعضهما البعض.
ومن خلال معادلة الانحدار يمكن عمل ما يلي:
- تحليل الانحدار: تحديد شكل العلاقة بين المتغيرين رياضيًا وبيانيًا.
- رسم خط الانحدار: توضيح اتجاه العلاقة بين المتغيرين على الرسم البياني.
- التنبؤ بقيمة أحد المتغيرين بدلالة المتغير الآخر، وذلك بالتعويض عن قيمة المتغير المعلوم في العلاقة أو المعادلة الرياضية وحساب قيمة المتغير الثاني فيها.
والانحدار له عدة أنواع، وهي:
- الانحدار الخطي البسيط
- الانحدار المتعدد
- الانحدار غير الخطي
وفيما يلا وصفًا موجزًا لكل منها:
الانحدار الخطي البسيط
الانحدار الخطي البسيط بين متغيرين هو الانحدار الذي يكون فيه المتغير الأول (المتغير التابع) مرتبطًا بمتغير ثاني وحيد (المتغير المستقل) من خلال علاقة رياضية خطية، أي أنهما مرتبطان معًا بعلاقة رياضية من الدرجة الأولى.
مثلا، العلاقة الرياضية التالية:
ص = أ + ب × س
تُمثل علاقة انحدار خطي بين المتغيرين: س، ص
وذلك لأنها تُعبر عن معادلة أو علاقة خطية (خالية من س2، س3، …، إلخ).
تمثيل الانحدار بالرسم البياني
من معادلة الانحدار الخطي:
ص = أ + ب × س
يمكن رسم خط بياني يمثل العلاقة الخطية بين المتغيرين (س) و(ص)، كما يلي:
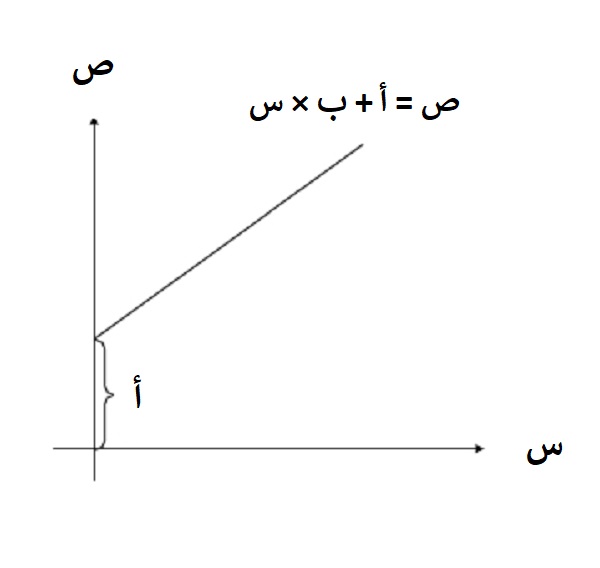
حيث أن:
- أ = ثابت الانحدار أو الجزء المقطوع من محور (ص)
- ب = ميل الانحدار أو مُعامل انحدار (ص) على (س)
الانحدار المتعدد
الانحدار المتعدد هو الانحدار الذي يرتبط فيه المتغير التابع بأكثر من متغير مستقل.
مثلا، العلاقة الرياضية التالية تُمثل علاقة انحدار متعدد بين س، ص، ع:
ص = أ + ب × س + ج × ع
الانحدار غير الخطي
الانحدار غير الخطي هو الانحدار الذي يكون فيه المتغير التابع مرتبطًا بالمتغير المستقل بعلاقة رياضية غير خطية، كأن تكون مثلا علاقة رياضية من الدرجة الثانية أو من النوع الأسي (أي أنها تحتوي على سن).
استخدام الانحدار في التنبؤ
نفرض أن لدينا متغيرين مرتبطين بعلاقة انحدار خطي من خلال العلاقة أو المعادلة الرياضية التالية:
ص = 3 + 4 × س
فإنه يمكن التنبؤ بقية المتغير (ص) عند معرفة قيمة المتغير (س) باستخدام العلاقة الرياضية التي تربط بينهما، وذلك كما يلي:
إذا علمنا أن (س = 20)، نقوم بالتعويض عن قيمة (س) في معادلة الانحدار، فيكون لدينا:
ص = 3 + 4 × 20
أو:
ص = 83
وهكذا لكل قيمة للمتغير المستقل (س) يمكن معرفة القيمة المُناظرة للمتغير التابع (ص).
المصدر
- كتاب التحليل المتقدم وتنقيب البيانات، د. م. مصطفى عبيد، دار الفكر العربي، القاهرة، جمهورية مصر العربية، الطبعة الأولى، 2017م.
- كتاب مهارات البحث العلمي، د.م. مصطفى فؤاد عبيد، مركز البحوث والدراسات متعدد التخصصات، الطبعة الثانية، إسطنبول، تركيا، 2022م.






