الارتباطات ثنائية المتغير
يحسب إجراء الارتباطات ثنائية المتغير Bivariate Correlations الارتباطات الزوجية لمجموعة من المتغيرات ويعرض النتائج في مصفوفة. يفيد هذا الإجراء في تحديد قوة واتجاه الارتباط بين متغيرين مقياسين scale أو متغيرين ترتيبيين ordinal.
مثال دراسة الارتباط بين مبيعات السيارات وكفاءة الوقود
من أجل زيادة المبيعات، يرغب مهندسو تصميم السيارات في تركيز انتباههم على جوانب السيارة المهمة للعملاء، على سبيل المثال، ما مدى أهمية كفاءة استهلاك الوقود فيما يتعلق بالمبيعات؟ تتمثل إحدى طرق قياس ذلك في حساب الارتباط بين المبيعات السابقة وكفاءة الوقود.
يتم جمع المعلومات المتعلقة بمختلف أنواع السيارات في ملف car_sales.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات. استخدم الارتباطات ثنائية المتغير Bivariate Correlations لقياس أهمية كفاءة الوقود في قابلية بيع السيارة.
تشغيل تحليل الارتباطات ثنائية المتغير
لإجراء تحليل الارتباطات ثنائية المتغير:
1. اختر من القوائم: تحليل> ارتباط> ثنائي المتغير …
Analyze > Correlate > Bivariate…
يظهر مربع حوار الارتباطات ثنائية المتغير Bivariate Correlations، ويتم من خلاله تحديد متغيرات “المبيعات بالآلاف” و”كفاءة الوقود” للتحليل، كما يلي:
2. حدد المبيعات بالآلاف Sales in thousands وكفاءة الوقود Fuel efficiency كمتغيرات تحليل variables.
3. انقر فوق “موافق” OK.
نتائج مصفوفة الارتباط
الشكل التالي يبين مصفوفة الارتباط من إجراء الارتباطات ثنائية المتغير، بين المبيعات بالآلاف Sales in thousands وكفاءة الوقود Fuel efficiency:
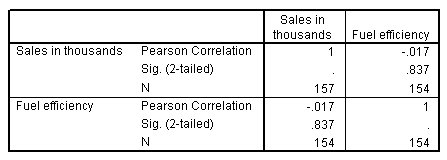
يقيس معامل ارتباط بيرسون Pearson correlation coefficient الارتباط الخطي بين متغيرين من نوع متغيرات المقياس scale variables. الارتباط المذكور في الجدول سالب (!)، على الرغم من أنه لا يختلف اختلافًا كبيرًا عن 0 لأن القيمة الاحتمالية p-value لـ 0.837 أكبر من 0.10. يشير هذا إلى أنه لا ينبغي للمصممين تركيز جهودهم على جعل السيارات أكثر كفاءة في استهلاك الوقود لأنه لا يوجد تأثير ملموس على المبيعات.
ومع ذلك، فإن معامل ارتباط بيرسون يعمل بشكل أفضل عندما تكون المتغيرات موزعة بشكل طبيعي تقريبًا ولا تحتوي على قيم متطرفة outliers. يمكن أن يكشف مخطط الانتشار scatterplot عن هذه المشاكل المحتملة.
إنشاء مخطط الانتشار
لإنتاج مخطط الانتشار للمبيعات بالآلاف بحسب كفاءة استهلاك الوقود:
1. اختر من القوائم: الرسوم البيانية> منشئ المخطط …
Graphs > Chart Builder…
يظهر منشئ المخطط البياني Chart Builder كما يلي:
2. حدد معرض “مبعثر/نقطة” Scatter/Dot واختر مبعثر بسيط Simple Scatter.
3. حدد المبيعات بالآلاف Sales in thousands كمتغير ص y variable وكفاءة الوقود Fuel efficiency كمتغير س x variable.
4. انقر فوق علامة التبويب “المجموعات/معرّف النقطة” Groups/Point ID وحدد Point ID Label.
5. حدد النموذج Model كمتغير لتسمية الحالات حسب variable to label cases by.
6. انقر فوق “موافق” OK.
الشكل التالي يبين نتيجة مخطط الانتشار Scatterplot للمبيعات وكفاءة الوقود:
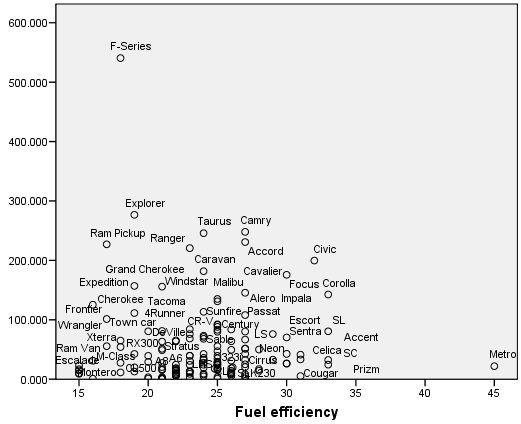
يُظهر مخطط الانتشار الناتج قيمتين شاذتين محتملتين، Metro في أسفل يمين المخطط وF-Series في أعلى اليسار.
تم العثور على F-Series لتكون ممثلة بشكل عام للمركبات التي يعمل عليها فريق التصميم لديك، لذلك قررت الاحتفاظ بها في مجموعة البيانات في الوقت الحالي. قد تبدو هذه النقطة متقطعة بسبب التوزيع الملتوي skew distribution للمبيعات بالآلاف، لذا حاول استبدالها بالمبيعات المحولة Log-transformed sales في مزيد من التحليلات. لا يمثل Metro المركبات التي يعمل عليها فريق التصميم لديك، لذا يمكنك إزالتها بأمان من التحليلات الإضافية.
تحسين تقديرات الارتباط بإزالة القيم المتطرفة
لإزالة Metro من حسابات الارتباط:
1. اختر من القوائم: البيانات> تحديد الحالات …
Data > Select Cases…
يظهر مربع حوار تحديد الحالات Select Cases، ويتم من خلاله اختيار الحالات بناءً على استيفاء شرط يتم تحديده، كما يلي:
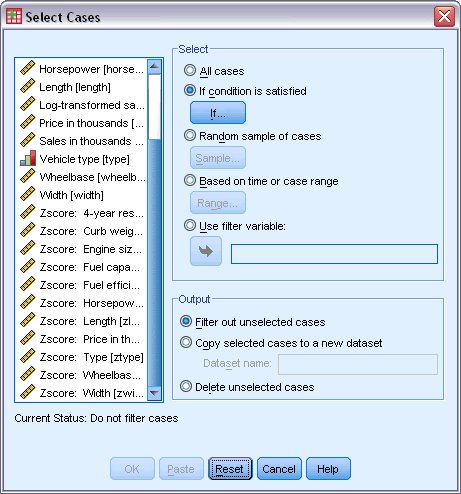
2. حدد “إذا تم استيفاء الشرط” If condition is satisfied وانقر فوق “إذا” If.
يظهر مربع حوار تحديد الحالات – إذا” Select Cases If dialog box لاختيار الحالات التي ليست Metro، كما يلي:
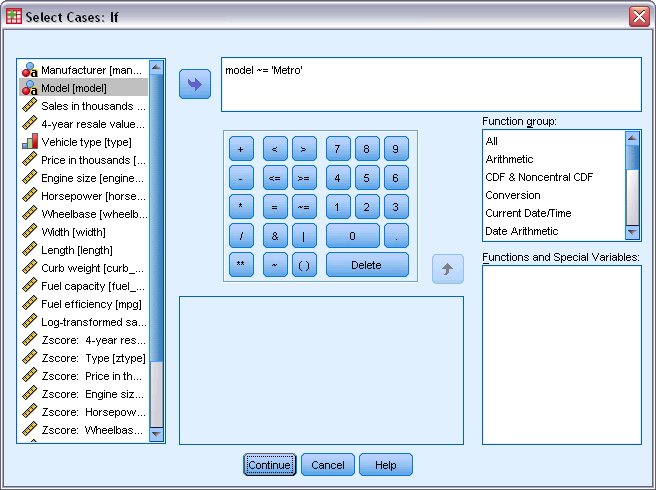
3. اكتب model ~= ‘Metro’ في مربع النص.
4. انقر فوق متابعة Continue.
5. انقر فوق “موافق” OK في مربع الحوار “تحديد الحالات” Select Cases.
يتم إنشاء متغير جديد يستخدم جميع الحالات باستثناء Metro في الحسابات التالية.
6. لتحليل البيانات التي تمت تصفيتها، قم باستدعاء مربع حوار الارتباطات ثنائية المتغير Bivariate Correlations.
يظهر مربع حوار الارتباطات ثنائية المتغير، ويتم من خلاله اختيار كفاءة الوقود والمبيعات المحولة من أجل التحليل، كما يلي:
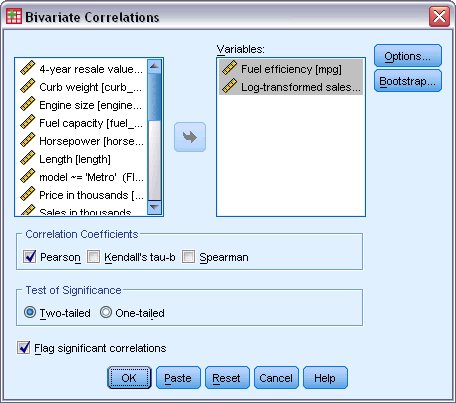
7. قم بإلغاء تحديد المبيعات بالآلاف Sales in thousands كمتغير تحليل analysis variable.
8. حدد المبيعات المحولة Log-transformed sales كمتغير تحليل analysis variable.
9. انقر فوق موافق OK.
نتائج تحليل الارتباطات
الشكل التالي يبين مصفوفة الارتباط للمبيعات المحولة Log-transformed sales حسب كفاءة الوقود Fuel efficiency:
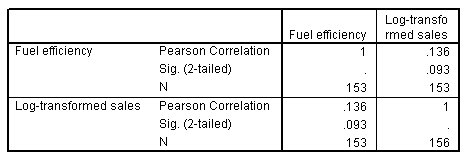
بعد إزالة القيمة المتطرفة outlier والنظر في المبيعات المحولة log-transformed sales، أصبح الارتباط الآن إيجابيًا ولكنه لا يزال لا يختلف كثيرًا عن 0.
ومع ذلك، فإن التركيبة السكانية للعملاء الذين يشترون الشاحنات trucks والسيارات automobiles مختلفة، وقد لا تكون أسباب شراء شاحنة أو سيارة هي نفسها. من المفيد إلقاء نظرة على مخطط انتشار آخر، ولكن هذه المرة مع تمييز الشاحنات والسيارات بشكل منفصل.
إنشاء مخطط الانتشار
لإنتاج مخطط انتشار scatterplot للمبيعات المحولة بحسب كفاءة الوقود، مع التحكم في نوع السيارة:
1. قم باستدعاء منشئ المخططات Chart Builder.
يظهر منشئ المخططات كما يلي:
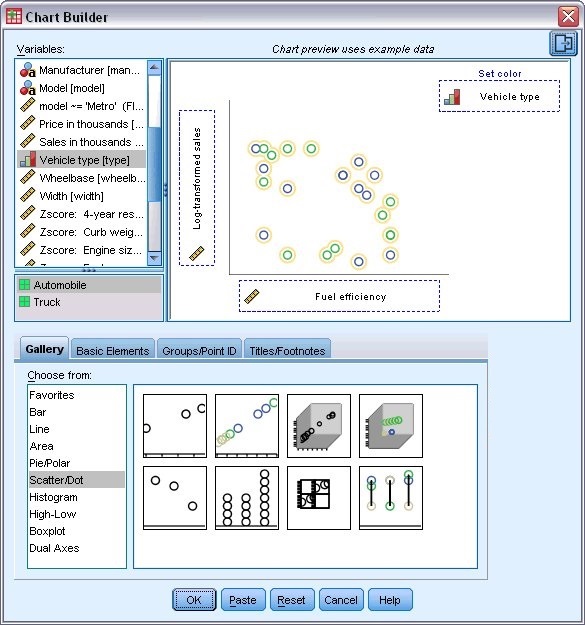
2. حدد “انتشار مجمع” Grouped Scatter.
3. حدد المبيعات المحولة Log-transformed sales كمتغير y.
4. حدد نوع المركبة Vehicle type كمتغير لضبط الألوان على أساسها to set colors by.
5. انقر فوق موافق OK.
الشكل التالي يبين نتيجة مخطط انتشار المبيعات المحولة بحسب كفاءة الوقود:
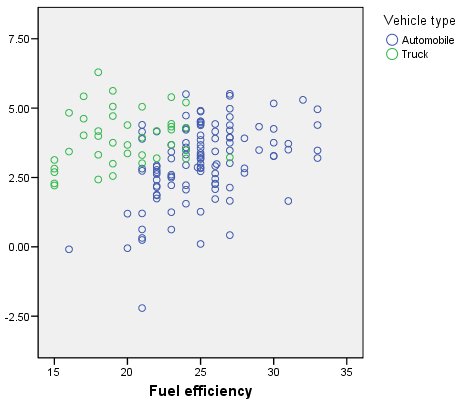
في الشكل أعلاه، مخطط انتشار المبيعات المحولة بحسب كفاءة استهلاك الوقود. هناك نوعان من الغيوم المتميزة إحداهما خاصة بالسيارات cars والأخرى للشاحنات trucks. هناك ميل إيجابي واضح لسحابة النقاط المقابلة للسيارات، ولا يوجد شكل واضح للسحابة المقابلة للشاحنات.
يوضح مخطط الانتشار أن الشاحنات والسيارات تشكل مجموعات مختلفة بشكل واضح. من خلال تقسيم ملف البيانات وفقًا لنوع السيارة Vehicle type، قد تحصل على عرض أكثر دقة للارتباط. لاحظ أيضًا أنه بعد تحويل المبيعات، اختفى التطرف المحتمل potential outlier في الجزء العلوي الأيسر.
تحسين تقديرات الارتباط من خلال تقسيم ملف البيانات
لتقسيم ملف البيانات حسب نوع السيارة Vehicle type:
1. اختر من القوائم: البيانات> تقسيم الملف …
Data > Split File…
يظهر مربع حوار تقسيم الملف Split File كما يلي:
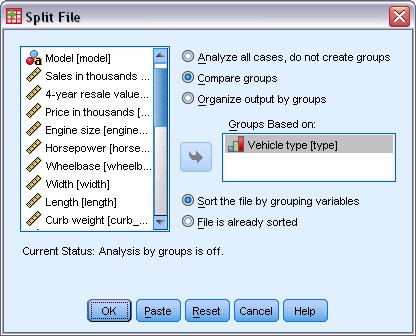
2. حدد مقارنة المجموعات Compare groups.
3. حدد نوع السيارة Vehicle type باعتباره المتغير الذي يجب أن تستند إليه المجموعات.
4. انقر فوق موافق OK.
5. لتحليل ملف الانقسام، قم باستدعاء مربع الحوار الارتباطات ثنائية المتغير Bivariate Correlations.
6. انقر فوق موافق OK.
نتائج تحليل الارتباطات
الشكل التالي يبين مصفوفة الارتباط الخاصة بكفاءة الوقود والمبيعات المحولة، مقسمة حسب نوع السيارة:
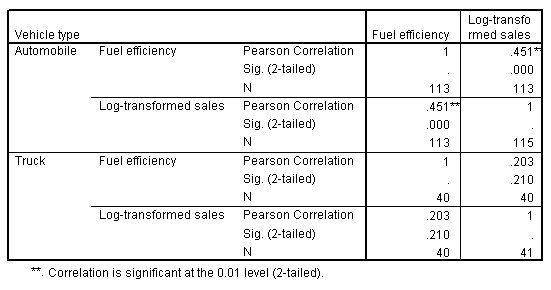
أدى تقسيم الملف بحسب نوع السيارة إلى جعل العلاقة بين المبيعات وكفاءة الوقود أكثر وضوحًا. هناك علاقة إيجابية مهمة وقوية إلى حد ما بين المبيعات وكفاءة استهلاك الوقود للسيارات automobiles. بالنسبة للشاحنات trucks، فإن الارتباط موجبًا ولكنه لا يختلف كثيرًا عن 0.
تطلب الوصول إلى هذه الاستنتاجات بعض العمل والجهد، وقد أظهر ذلك أن تحليل الارتباط باستخدام معامل ارتباط بيرسون ليس دائمًا مباشرًا. لعمل مقارنة، انظر الفقرة التالية كيف يمكنك تجنب صعوبة تحويل المتغيرات باستخدام مقاييس الارتباط اللامعلمية nonparametric correlation.
تقديرات الارتباطات ثنائية المتغير اللامعلمية
تقيس إحصائيات معامل ارتباط سبيرمان Spearman’s rho و Kendall’s tau-b ارتباط “ترتيب الترتيب” rank-order بين متغيرين مقياسين scale أو متغيرين ترتيبيين ordinal. إنها تعمل بغض النظر عن توزيعات المتغيرات.
للحصول على تحليل باستخدام ارتباط سبيرمان Spearman’s rho:
1. قم باستدعاء مربع حوار الارتباطات ثنائية المتغير Bivariate Correlations.
2. حدد المبيعات بالآلاف Sales in thousands كمتغير تحليل analysis variable.
3. قم بإلغاء تحديد بيرسون Pearson وحدد سبيرمان Spearman.
4. انقر فوق موافق OK.
مربع حوار الارتباطات ثنائية المتغير، مع اختيار كفاءة الوقود والمبيعات المحولة من أجل التحليل، وتحديد مقياس سبيرمان للارتباط.
نتائج تحليل الارتباطات ثنائية المتغير
الشكل التالي يبين مصفوفة الارتباط لكفاءة الوقود والمبيعات المحولة، مقسمة حسب نوع السيارة Vehicle type، باستخدام معامل ارتباط سبيرمان رو Spearman’s rho كمقياس للارتباط.
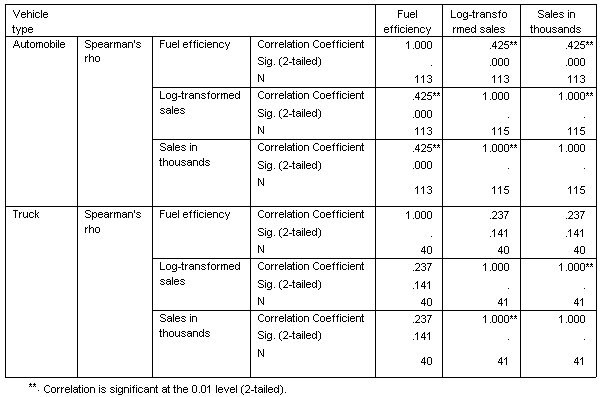
يتم التقرير عن ارتباط سبيرمان Spearman’s rho بشكل منفصل للسيارات automobiles والشاحنات trucks. كما هو الحال مع معامل ارتباط بيرسون Pearson’s correlation، فإن الارتباط بين المبيعات المحولة وكفاءة الوقود قوي إلى حد ما. ومع ذلك، فإن معامل ارتباط رو سبيرمان Spearman’s rho يبين نفس الارتباط للمبيعات غير المحولة! هذا لأن رو rho يعتمد على ترتيب الترتيب rank orders، والذي لم يتغير عن طريق التحويل. علاوة على ذلك، فإن القيم المتطرفة outliers لها تأثير أقل على معامل سبيرمان، لذلك من الممكن توفير بعض الوقت والجهد باستخدامها كمقياس للارتباط بدلا من استخدام معامل بيرسون هنا.
ملخص التطبيق العملي لاستخدام الارتباطات ثنائية المتغير
باستخدام الارتباطات ثنائية المتغير Bivariate Correlations، أنتجت مصفوفة ارتباط للمبيعات بالآلاف بحسب كفاءة استخدام الوقود، ومن المدهش أنك وجدت ارتباطًا سلبيًا. عند إزالة القيم المتطرفة واستخدام المبيعات المحولة، أصبح الارتباط إيجابيًا، على الرغم من أنه لا يختلف كثيرًا عن 0. ومع ذلك، وجدت أنه من خلال حساب الارتباطات بشكل منفصل للشاحنات والسيارات، هناك علاقة إيجابية ودلالة إحصائية بين المبيعات وكفاءة استخدام الوقود للسيارات.
علاوة على ذلك، لقد وجدت نتائج مماثلة بدون إجراء التحويل باستخدام معامل سبيرمان للارتباط Spearman’s rho، وربما تتساءل لماذا يجب عليك بذل جهد لتحويل المتغيرات عندما يكون معامل سبيرمان Spearman’s rho مناسبًا جدًا. تعتبر مقاييس ترتيب الترتيب مفيدة لاكتشاف ما إذا كان هناك أي نوع من الارتباط بين متغيرين، ولكن عندما يوجد ارتباطًا، فمن الجيد إيجاد تحويل ما بحيث يجعل العلاقة خطية. هذا بسبب وجود المزيد من النماذج التنبؤية المتاحة للعلاقات الخطية، كما أن النماذج الخطية أسهل في التنفيذ والتفسير بشكل عام.
الإجراءات ذات الصلة
يعتبر إجراء الارتباطات ثنائية المتغير مفيدًا لدراسة الارتباطات الزوجية لمجموعة من المتغيرات من نوع المقياس أو المتغيرات الترتيبية.
- إذا كان لديك متغيرات اسمية، فاستخدم الإجراء تحليل تقاطعات البيانات Crosstabs للحصول على مقاييس الارتباط.
- إذا كنت تريد تصميم قيمة متغير مقياس بناءً على علاقته الخطية بالمتغيرات الأخرى، فجرّب إجراء الانحدار الخطي Linear Regression.
- أما إذا كنت تريد تحليل التباين في بياناتك للبحث عن الأنماط الأساسية، فجرّب إجراء تحليل العوامل Factor Analysis.
المصدر
- كتاب التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- الموقع الرسمي لشركة IBM ® برنامج SPSS