ما هو الاحتكاك
عندما يتحرك الجسم، يكون لديه مقاومة لأن الجسم يتفاعل مع محيطه. هذه المقاومة هي قوة الاحتكاك. يتعارض الاحتكاك مع الحركة النسبية بين الأنظمة المتلامسة ولكنه يسمح لنا أيضًا بالتحرك، وهو مفهوم يصبح واضحًا إذا حاولت المشي على الجليد. الاحتكاك قوة شائعة ومعقدة، ولا يزال سلوكها غير مفهوم تمامًا. ومع ذلك، من الممكن فهم الظروف التي يتصرف فيها.
أهداف التعلم
بنهاية هذا القسم، ستكون قادرًا على:
- وصف الخصائص العامة للاحتكاك.
- وضع قائمة بأنواع الاحتكاك المختلفة.
- حساب مقدار الاحتكاك السكوني والحركي، واستخدمهما في المسائل التي تتضمن قوانين نيوتن للحركة.
المحتويات
الاحتكاك الساكن والاحتكاك الحركي
التعريف الأساسي للاحتكاك بسيط نسبيًا.
الاحتكاك (بالإنجليزية: Friction) هو قوة تعارض الحركة النسبية بين الأنظمة المتلامسة.
هناك عدة أشكال من الاحتكاك. من أبسط خصائص الاحتكاك الانزلاقي أنه موازٍ لأسطح التلامس بين الأنظمة ودائمًا ما يكون في اتجاه يعارض الحركة أو محاولة الحركة للأنظمة بالنسبة لبعضها البعض.
إذا كان نظامان على اتصال ويتحركان بالنسبة لبعضهما البعض، فإن الاحتكاك بينهما يسمى الاحتكاك الحركي. على سبيل المثال، يؤدي الاحتكاك إلى إبطاء انزلاق قرص الهوكي على الجليد. عندما تكون الأجسام ثابتة، يمكن أن يعمل الاحتكاك الساكن بينها؛ عادة ما يكون الاحتكاك الساكن أكبر من الاحتكاك الحركي بين جسمين.
تعريف الاحتكاك الساكن والحركي
إذا كان نظامان على اتصال وثابتين بالنسبة لبعضهما البعض، فإن الاحتكاك بينهما يسمى الاحتكاك الساكن. وإذا كان نظامان على اتصال ويتحركان بالنسبة لبعضهما البعض، فإن الاحتكاك بينهما يسمى الاحتكاك الحركي.
تخيل، على سبيل المثال، محاولة دفع صندوق ثقيل عبر أرضية خرسانية – قد تدفع بقوة على الصندوق ولا تحركه على الإطلاق. هذا يعني أن الاحتكاك الساكن يستجيب لما تفعله – يزداد ليصبح مساويًا للقوة في الاتجاه المعاكس لدفعك وفي الاتجاه المعاكس لها. إذا ضغطت أخيرًا بقوة كافية، يبدو أن الصندوق ينزلق فجأة ويبدأ في التحرك. الآن الاحتكاك الساكن يفسح المجال للاحتكاك الحركي. بمجرد بدء الحركة، يكون من الأسهل إبقائها في حالة حركة أكثر مما كانت عليه في البداية، مما يشير إلى أن قوة الاحتكاك الحركي أقل من قوة الاحتكاك الساكن. إذا أضفت كتلة إلى الصندوق، على سبيل المثال عن طريق وضع صندوق فوقه، فأنت بحاجة إلى الضغط بقوة أكبر لبدء تحريكه وكذلك لإبقائه متحركًا. علاوة على ذلك، إذا قمت بدهن الخرسانة بالزيت، فستجد أنه من الأسهل بدء تحريك الصندوق واستمراره في الحركة (كما قد تتوقع).
شكل 6.10: تمثيل تصويري خام لكيفية حدوث الاحتكاك عند السطح البيني بين جسمين. يظهر الفحص عن قرب لهذه الأسطح أنها خشنة. وبالتالي، عندما تضغط لتحريك جسم ما (في هذه الحالة، صندوق)، يجب عليك رفع الجسم حتى يتمكن من تخطيه جنبًا إلى جنب مع أطراف السطح التي تضرب أو تقطع النقاط أو كليهما. يمكن مقاومة قوة كبيرة بالاحتكاك بدون حركة ظاهرة. كلما زادت صعوبة دفع الأسطح معًا (مثل وضع صندوق آخر على الصندوق)، زادت القوة اللازمة لتحريكها. يرجع جزء من الاحتكاك إلى قوى الالتصاق بين جزيئات السطح لكائنين، وهو ما يفسر اعتماد الاحتكاك على طبيعة المواد. على سبيل المثال، الأحذية ذات النعل المطاطي تنزلق أقل من الأحذية ذات النعال الجلدية. يختلف الالتصاق باختلاف المواد الملامسة وهو جانب معقد من فيزياء السطوح. بمجرد أن يتحرك الجسم، يكون هناك عدد أقل من نقاط التلامس (عدد أقل من الجزيئات الملتصقة)، لذا فإن الأمر يتطلب قوة أقل للحفاظ على حركة الجسم. عند السرعات الصغيرة ولكن غير الصفرية، يكون الاحتكاك مستقلاً تقريبًا عن السرعة.
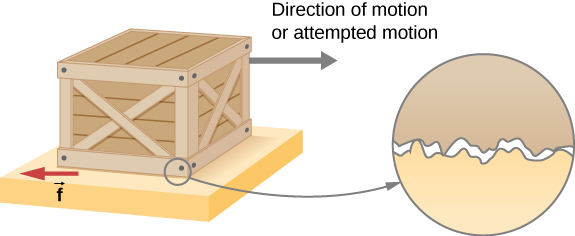
شكل 6.10: قوى الاحتكاك، مثل F⃗ تعارض دائمًا الحركة أو محاولة الحركة بين الأشياء المتلامسة. ينشأ الاحتكاك جزئيًا بسبب خشونة الأسطح المتلامسة، كما يظهر في العرض الموسع. لكي يتحرك الكائن، يجب أن يرتفع إلى حيث يمكن أن تتخطى قمم السطح العلوي على طول السطح السفلي. بالتالي، فإن القوة مطلوبة فقط لتحريك الجسم. سيتم قطع بعض القمم، مما يتطلب أيضًا قوة للحفاظ على الحركة. يرجع جزء كبير من الاحتكاك في الواقع إلى قوى الجذب بين الجزيئات المكونة للكائنين، بحيث لا تكون الأسطح الملساء تمامًا خالية من الاحتكاك. في الواقع، سوف تلتصق الأسطح النظيفة والنظيفة تمامًا من مواد مماثلة، وتشكل رابطة تسمى “اللحام البارد”.
لمقدار قوة الاحتكاك شكلين: أحدهما للحالات الساكنة (الاحتكاك الساكن)، والأخرى للحالات التي تنطوي على حركة (الاحتكاك الحركي). ما يلي هو نموذج تجريبي تقريبي (تم تحديده تجريبيًا) فقط. هذه المعادلات الخاصة بالاحتكاك الساكن والحركي ليست معادلات متجهة.
مقدار الاحتكاك الساكن
مقدار الاحتكاك الساكن Fs سيكون
fs ≤ μs N
(6.1)
حيث: μs هو معامل الاحتكاك الساكن. وN هي مقدار القوة العمودية.
الرمز ≤ يعني أقل من أو يساوي، مما يعني أن الاحتكاك الساكن يمكن أن يكون له قيمة قصوى تبلغ قيمتها μs N.
الاحتكاك الساكن هو قوة استجابة تزداد لتكون مساوية ومعاكسة لأي قوة تمارس، حتى أقصى حد لها. وبمجرد أن تتجاوز القوة المطبقة الحد الأقصى fs (max)، يتحرك هذا الكائن. وهكذا، يكون:
fs (max) = μs N
مقدار الاحتكاك الحركي
مقدار الاحتكاك الحركي fk يُعطي من خلال المعادلة التالية:
fk = μk N
(6.2)
حيث: μk هو معامل الاحتكاك الحركي.
أي نظام يكون فيه fk = μk N يوصف بأنه نظام يتصرف فيه الاحتكاك ببساطة.
يوضح شكل 6.11 الانتقال من الاحتكاك الساكن إلى الاحتكاك الحركي.
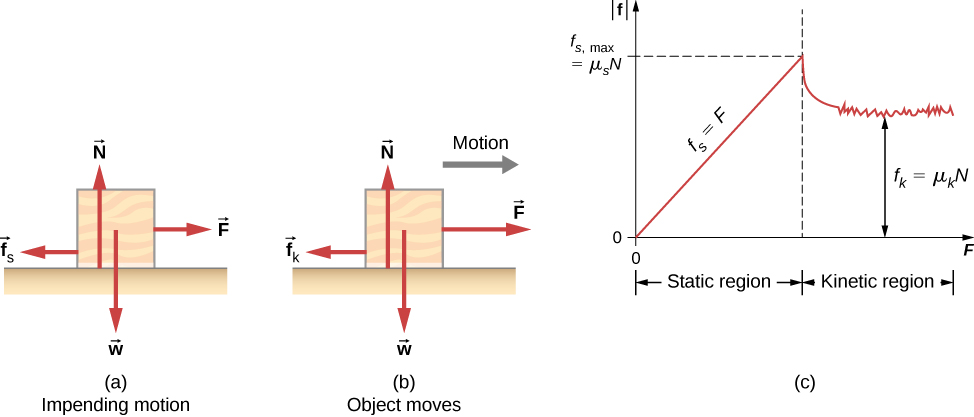
شكل 6.11: (أ) قوة الاحتكاك F⃗ بين الكتلة والسطح الخشن تتعارض مع اتجاه القوة المطبقة F⃗. يوازن مقدار الاحتكاك الساكن مع القوة المطبقة. يظهر هذا في الجانب الأيسر من الرسم البياني في (ج). (ب) في مرحلة ما، يكون مقدار القوة المطبقة أكبر من قوة الاحتكاك الحركي، وتتحرك الكتلة إلى اليمين. يظهر هذا في الجانب الأيمن من الرسم البياني. (ج) الرسم البياني لقوة الاحتكاك مقابل القوة المطبقة.
لاحظ أن fs(max) > fk، وهذا يعني أن: μs > μk.
كما ترى في الجدول 6.1، معاملات الاحتكاك الحركي أقل من معاملات الاحتكاك الساكن المناظرة لنفس المادة. القيم التقريبية للمعامل μ تم كتابتها بالتقريب لأقرب رقم واحد أو رقمين عشريين للإشارة إلى الوصف التقريبي للاحتكاك المعطى بواسطة المعادلتين السابقتين.
| النظام | الاحتكاك الساكن | الاحتكاك الحركي |
| مطاط على الخرسانة الجافة | 1.0 | 0.7 |
| مطاط على الخرسانة الرطبة | 0.5-0.7 | 0.3-0.5 |
| خشب على خشب | 0.5 | 0.3 |
| خشب مشمع على ثلج مبلل | 0.14 | 0.1 |
| معدن على خشب | 0.5 | 0.3 |
| صلب على صلب (جاف) | 0.6 | 0.3 |
| الصلب على الصلب (يتأهل) | 0.05 | 0.03 |
| تفلون على الفولاذ | 0.04 | 0.04 |
| العظام المشحمة بواسطة السائل الزلالي | 0.016 | 0.015 |
| أحذية على الخشب | 0.9 | 0.7 |
| أحذية على الجليد | 0.1 | 0.05 |
| جليد على جليد | 0.1 | 0.03 |
| صلب على الجليد | 0.4 | 0.02 |
تتضمن المعادلة 6.1 والمعادلة 6.2 اعتماد الاحتكاك على المواد والقوة العادية. يكون اتجاه الاحتكاك دائمًا معاكسًا لاتجاه الحركة، ويكون موازيًا للسطح بين الأجسام، وعموديًا على القوة العمودية. على سبيل المثال، إذا كان الصندوق الذي تحاول دفعه (بقوة موازية للأرض) كتلته 100 كجم، فإن القوة العادية تساوي وزنه:
w = m g = (100kg)(9.80 m/s2) = 980 N
عمودي على الأرض. إذا كان معامل الاحتكاك الساكن يساوي 0.45، فسيتعين عليك بذل قوة موازية للأرض أكبر من:
fs (max) = μs N = (0.45)(980N) = 440 N
لتحريك الصندوق.
بمجرد وجود حركة، يكون الاحتكاك أقل وقد يكون معامل الاحتكاك الحركي 0.30، بحيث تكون قوة مقدارها فقط:
fk = μk N = (0.30)(980N) = 290 N
تبقيها تتحرك بسرعة ثابتة.
إذا تم تشحيم الأرضية، يكون كلا المعاملين أقل بكثير مما سيكون عليه بدون تشحيم أو تزييت. معامل الاحتكاك هو كمية غير محددة مقدارها عادة بين 0 و1.0. تعتمد القيمة الفعلية على السطحين المتصلين.
عانى الكثير من الناس من انزلاق المشي على الجليد. ومع ذلك، فإن العديد من أجزاء الجسم، وخاصة المفاصل، لها معاملات احتكاك أصغر بكثير – غالبًا ما تكون أقل بثلاث أو أربع مرات من الجليد. يتكون المفصل من نهايات عظمتين متصلتين بأنسجة سميكة. يتكون مفصل الركبة من عظم الساق (عظمة القصبة) وعظم الفخذ. الورك عبارة عن كرة (في نهاية عظم الفخذ) ومقبس (جزء من الحوض). نهايات العظام في المفصل مغطاة بالغضروف، مما يوفر سطحًا أملسًا شبه زجاجي. تنتج المفاصل أيضًا سائلًا (سائلًا زليليًا) يقلل الاحتكاك والتآكل. يمكن استبدال المفصل التالف أو الملتهب بمفصل اصطناعي ( الشكل 6.12.2). يمكن أن تكون هذه البدائل مصنوعة من معادن (الفولاذ المقاوم للصدأ أو التيتانيوم) أو البلاستيك (البولي إيثيلين)، أيضًا مع معاملات احتكاك صغيرة جدًا.
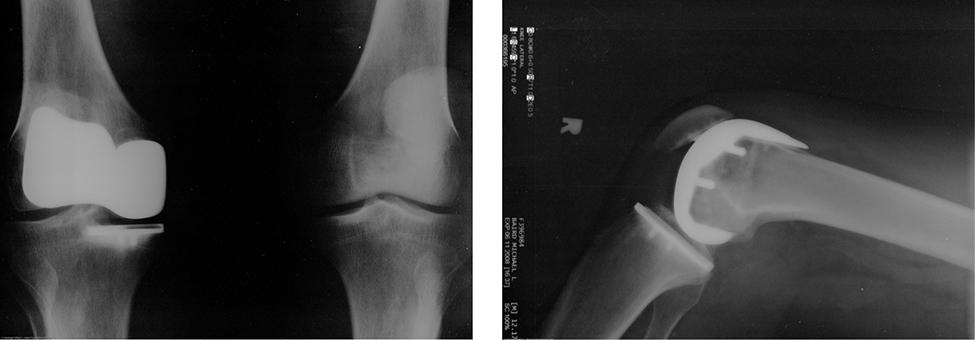
شكل 6.12: الاستبدال الاصطناعي للركبة هو إجراء تم إجراؤه لأكثر من 20 عامًا. تظهر هذه الأشعة السينية بعد الجراحة استبدال مفصل الركبة اليمنى (المصدر: بواسطة مايك بيرد).
تشتمل المزلقات الطبيعية على اللعاب المنتج في أفواهنا للمساعدة في عملية البلع، والمخاط الزلق الموجود بين أعضاء الجسم، مما يسمح لها بالتحرك بحرية فوق بعضها البعض أثناء ضربات القلب، وأثناء التنفس، وعندما يتحرك الشخص. عادةً ما تستخدم المستشفيات وعيادات الأطباء المزلقات الاصطناعية، مثل المواد الهلامية، لتقليل الاحتكاك.
المعادلات المعطاة للاحتكاك الساكن والحركي هي قوانين تجريبية تصف سلوك قوى الاحتكاك. في حين أن هذه الصيغ مفيدة جدًا للأغراض العملية، إلا أنها لا تتمتع بوضع البيانات الرياضية التي تمثل المبادئ العامة (على سبيل المثال، قانون نيوتن الثاني). في الواقع، هناك حالات لا تعتبر فيها هذه المعادلات التقريبية جيدة. على سبيل المثال، لا تعد أي من الصيغتين دقيقة بالنسبة للأسطح المشحمة أو لسطحين ينزلقان عبر بعضهما البعض بسرعات عالية. ما لم يتم تحديد ذلك، لن نهتم بهذه الاستثناءات.
مثال 6.10: الاحتكاك الساكن والحركي
صندوق يزن 20.0 كجم في وضع السكون على الأرضية كما هو موضح في الشكل 6.13. معامل الاحتكاك الساكن بين الصندوق والأرض هو 0.7، ومعامل الاحتكاك الحركي هو 0.6. قوة أفقية f⃗ يتم تطبيقها على الصندوق. أوجد قوة الاحتكاك إذا كان:
- P⃗ =20.0Niˆ
- P⃗ =30.0Niˆ
- P⃗ =120.0Niˆ
- P⃗ =180.0Niˆ
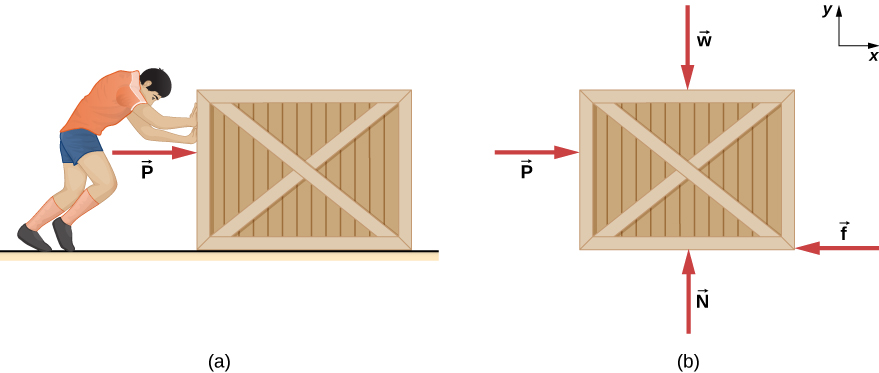
شكل 6.13: (أ) صندوق على سطح أفقي مدفوع بقوة f⃗. (ب) القوى الموجودة على الصندوق. هنا، F⃗ تمثل القوة الاحتكاكية الساكنة أو الحركية.
استراتيجية الحل
يظهر مخطط الجسم الحر للصندوق في الشكل 6.13 (ب). نطبق قانون نيوتن الثاني في الاتجاهين الأفقي والعمودي، بما في ذلك قوة الاحتكاك في معارضة اتجاه حركة الصندوق.
الحل
يعطي قانون نيوتن الثاني:
∑ Fx = m ax
P – f = m ax
∑ Fy = m ay
N – w = 0
نحن هنا نستخدم الرمز f لتمثيل قوة الاحتكاك لأننا لم نحدد بعد ما إذا كان الصندوق معرضًا لاحتكاك المحطة أو الاحتكاك الحركي. نفعل هذا عندما نكون غير متأكدين من نوع الاحتكاك الذي يعمل.
الآن وزن الصندوق هو:
W = (20.0kg)(9.80m/s2) = 196 N
وهو أيضًا يساوي N. وبالتالي، فإن أقصى قوة للاحتكاك الساكن هي:
(0.700)(196N) = 137 N
طالما P⃗ أقل من 137 نيوتن، فإن قوة الاحتكاك الساكن تُبقي الصندوق ثابتًا وfs = P⃗.
وهكذا، فإن:
(a) fs = 20.0 N
(b) fs = 30.0 N
and (c) fs = 120.0 N
واذا كان:
(d) If P⃗ = 180.0
فتكون القوة المطبقة أكبر من القوة القصوى للاحتكاك الساكن (137 نيوتن)، لذلك لم يعد بإمكان الصندوق البقاء في حالة سكون. وبمجرد أن يتحرك الصندوق، يعمل الاحتكاك الحركي. ثم يكون:
fk = μk N = (0.600)(196N) = 118 N
والتسارع يساوي:
ax = (P – fk) / m = (180.0 N – 118 N) / 20.0 kg = 3.10 m/s2
الدلالة
يوضح هذا المثال كيف ننظر إلى الاحتكاك في مسائل الديناميكا. لاحظ أن قيمة الاحتكاك الساكن تطابق القوة المطبقة، حتى نصل إلى الحد الأقصى لقيمة الاحتكاك الساكن. أيضًا، لا يمكن أن تحدث أي حركة حتى تساوي القوة المطبقة قوة الاحتكاك الساكن، لكن قوة الاحتكاك الحركي ستقل بعد ذلك.
تحقق من فهمك
كتلة كتلتها 1.0 كجم موضوعة على سطح أفقي. معاملات الاحتكاك للكتلة والسطح هي μs=0.50 وμk = 0.40.
(أ) ما هي القوة الأفقية الدنيا المطلوبة لتحريك الكتلة؟ (ب) ما عجلة الكتلة عند تطبيق هذه القوة؟
الاحتكاك والمستوى المائل
أحد المواقف التي يلعب فيها الاحتكاك دورًا واضحًا هو وجود جسم على منحدر. قد يكون صندوقًا يتم دفعه لأعلى منحدر إلى رصيف التحميل أو لوح تزلج ينحدر أسفل جبل، لكن في الحالتين فإن الفيزياء الأساسية هي نفسها. عادة ما نقوم بتعميم السطح المائل ونسميه المستوى المائل ولكن بعد ذلك نتظاهر بأن السطح مسطح. لنلقِ نظرة على مثال لتحليل الحركة على مستوى مائل مع وجود الاحتكاك.
مثال 6.11: انحدار المتزلج على الجليد
متزلج كتلته 62 كجم ينزلق على منحدر ثلجي بعجلة ثابتة (تسارع ثابت). أوجد معامل الاحتكاك الحركي للمتزلج إذا عرفت أن الاحتكاك يساوي 45.0 نيوتن.
استراتيجية الحل
مقدار الاحتكاك الحركي 45.0 نيوتن. يرتبط الاحتكاك الحركي بالقوة العادية N بواسطة المعادلة: fk = μk N. وهكذا، يمكننا إيجاد معامل الاحتكاك الحركي إذا تمكنا من إيجاد القوة العادية المؤثرة على المتزلج. تكون القوة الطبيعية أو العادية Normal دائمًا متعامدة على السطح، وبما أنه لا توجد حركة عمودية على السطح، يجب أن تساوي القوة العمودية مركب وزن المتزلج المتعامد مع المنحدر. انظر الشكل 6.14، الذي يكرر شكلاً من الفصل الخاص بقوانين نيوتن للحركة.
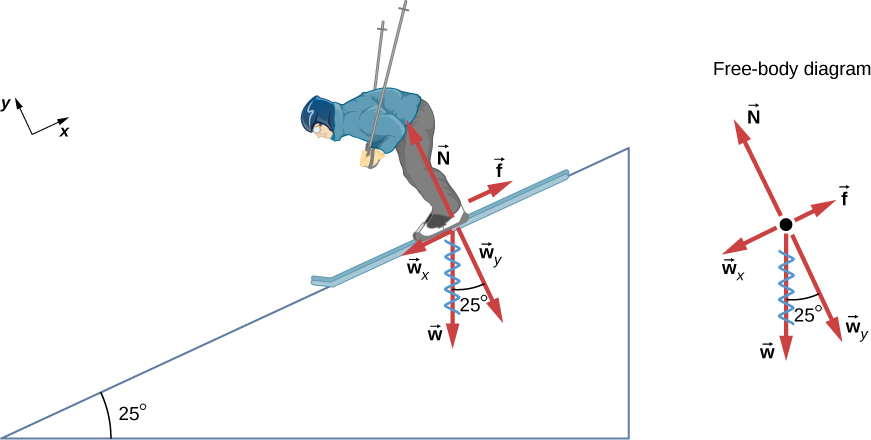
شكل 6.14: حركة المتزلج والاحتكاك موازيان للمنحدر، لذا فمن الأنسب عرض كل القوى على نظام إحداثيات حيث يكون أحد المحورين موازٍ للمنحدر والآخر متعامد عليه (تظهر المحاور على يسار المتزلج).
القوة الطبيعية N ⃗ عمودية على ميل المنحدر والاحتكاك F⃗ يوازي المنحدر، لكن وزن المتزلج w⃗ يحتوي على مكونات على طول كلا المحورين، وهما w⃗x وw⃗y. والقوة الطبيعية N تساوي من حيث المقدار الوزن w، لذلك لا توجد حركة عمودية على المنحدر.
لدينا:
N = wy = w cos 25° = m g cos 25°
نستبدل هذا في تعبيرنا عن الاحتكاك الحركي، نحصل على:
fk = μk m g cos 25°
والتي يمكن حلها الآن من أجل إيجاد معامل الاحتكاك الحركي μk.
الحل
بحل المعادلة وترتيبها من أجل إيجاد μk يكون:
μk = fk / N =fk / (w cos 25°) = fk / (m g cos 25°)
باستبدال القيم المعروفة على الجانب الأيمن من المعادلة:
μk = 45 N / ((62 kg)(9.8 m/s2)(0.906)) = 0.082
الدلالة
هذه النتيجة أصغر قليلاً من المعامل المدرج في الجدول 6.1 للخشب المشمع على الثلج، لكنها لا تزال معقولة نظرًا لأن قيم معاملات الاحتكاك يمكن أن تختلف اختلافًا كبيرًا.
في مثل هذه الحالات، عندما ينزلق جسم كتلته m على منحدر يصنع زاوية ثيتا θ مع الأفقي، يتم إعطاء الاحتكاك بواسطة المعادلة:
fk =μk m g cos θ
تنزلق جميع الكائنات على منحدر بتسارع ثابت في ظل هذه الظروف.
اشتقاق معادلة حساب الاحتكاك
لقد ناقشنا أنه عندما يستقر جسم على سطح أفقي، فإن القوة الطبيعية العمودية التي تدعمه تساوي وزنه في المقدار. علاوة على ذلك، فإن الاحتكاك البسيط يتناسب دائمًا مع القوة الطبيعية. عندما لا يكون الجسم على سطح أفقي، كما هو الحال مع المستوى المائل، يجب أن نجد القوة المؤثرة على الجسم الموجه عموديًا على السطح؛ وفي هذه الحالة فإنه يكون هو أحد مكوّنات الوزن.
نشتق الآن علاقة مفيدة لحساب معامل الاحتكاك على مستوى مائل. لاحظ أن النتيجة تنطبق فقط على المواقف التي ينزلق فيها الكائن بسرعة ثابتة أسفل المنحدر.
ينزلق جسم ما على مستوى مائل بسرعة ثابتة إذا كانت القوة الكلية المؤثرة عليه تساوي صفرًا. يمكننا استخدام هذه الحقيقة لقياس معامل الاحتكاك الحركي بين جسمين. كما هو موضح في المثال 6.11، فإن:
الاحتكاك الحركي على المنحدر هو:
fk = μk m g cos θ
وعنصر الوزن أسفل المنحدر يساوي:
m g sin θ
(انظر الرسم التخطيطي للجسم الحر في الشكل 6.14).
تعمل هذه القوى في اتجاهين متعاكسين، لذلك عندما يكون لها نفس المقدار، فإن العجلة تساوي صفرًا.
يمكن كتابة هذا كما يلي:
μk m g cos θ = m g sin θ
وبحل المعادلة، نجد أن:
μk = m g sin θ / m g cos θ = tan θ
ضع عملة معدنية على كتاب وقم بإمالته حتى تنزلق العملة المعدنية بسرعة ثابتة أسفل الكتاب. قد تحتاج إلى النقر على الكتاب برفق لتحريك العملة. قم بقياس زاوية الميل بالنسبة إلى الأفقي وإيجاد معامل الاحتكاك μk. لاحظ أن العملة لا تبدأ في الانزلاق على الإطلاق حتى زاوية أكبر من θ يتم الوصول إليها، وذلك لأن معامل الاحتكاك الساكن أكبر من معامل الاحتكاك الحركي. فكر في كيفية تأثير ذلك على قيمة معامل الاحتكاك μk وعدم التأكد منه.
تفسيرات النطاق الذري للاحتكاك
إن أبسط جوانب الاحتكاك التي تم التعامل معها حتى الآن هي خصائصه العينية (واسعة النطاق). لقد قُطعت خطوات كبيرة في تفسير المقياس الذري للاحتكاك خلال العقود العديدة الماضية. وقد وجد الباحثون أن الطبيعة الذرية للاحتكاك يبدو أن لها العديد من الخصائص الأساسية. لا تفسر هذه الخصائص بعض الجوانب الأبسط للاحتكاك فحسب بل إنها تمتلك أيضًا إمكانية تطوير بيئات خالية من الاحتكاك تقريبًا يمكن أن توفر مئات المليارات من الدولارات من الطاقة التي يتم تحويلها حاليًا (بدون داعٍ) إلى حرارة.
يوضح الشكل 6.15 إحدى الخصائص العيانية (العينية) للاحتكاك والتي تم تفسيرها من خلال البحث المجهري (على نطاق صغير). لقد لاحظنا أن الاحتكاك يتناسب طرديًا مع القوة العادية (الطبيعية)، ولكن ليس مع مقدار المنطقة الملامسة، وهي فكرة غير متوقعة إلى حد ما. عندما يتلامس سطحان خشنان، تكون منطقة التلامس الفعلية جزءًا صغيرًا من المساحة الكلية لأن النقاط العالية فقط هي التي تتلامس. عند ممارسة قوة طبيعية أكبر، تزداد منطقة التلامس الفعلية، ونجد أن الاحتكاك يتناسب مع هذه المنطقة.
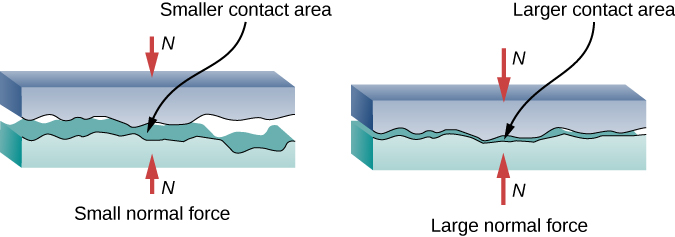
شكل 6.15: سطحان خشنان متصلان بهما مساحة أصغر بكثير من التلامس الفعلي من المساحة الإجمالية. عندما تكون القوة العادية أكبر نتيجة لقوة مطبقة أكبر، تزداد مساحة التلامس الفعلي، وكذلك الاحتكاك.
الاحتكاك والحرارة
ومع ذلك، فإن منظور المقياس الذري يعد بشرح أكثر بكثير من السمات الأبسط للاحتكاك. يتم الآن تحديد آلية كيفية توليد الحرارة. بمعنى آخر، لماذا تصبح الأسطح أكثر دفئًا عند الاحتكاك؟ بشكل أساسي، ترتبط الذرات ببعضها البعض لتشكيل مشابك. عندما تحتك الأسطح، تلتصق ذرات السطح وتتسبب في اهتزاز المشابك الذرية – مما ينتج عنه موجات صوتية تخترق المادة. تتضاءل الموجات الصوتية مع المسافة، وتتحول طاقتها إلى حرارة. يمكن أن تحدث التفاعلات الكيميائية المرتبطة بالتآكل الاحتكاكي أيضًا بين الذرات والجزيئات على الأسطح.
يوضح الشكل 6.16 كيف يتشوه رأس المسبار المرسوم عبر مادة أخرى بفعل الاحتكاك بالمقياس الذري. يمكن قياس القوة اللازمة لسحب الطرف ووجد أنها مرتبطة بها إجهاد القص، والذي تمت مناقشته في موضوع التوازن الثابت والمرونة. التباين في إجهاد القص ملحوظ (أكثر من معامل 10 12) ويصعب التنبؤ به نظريًا، لكن إجهاد القص ينتج عنه فهم أساسي لظاهرة واسعة النطاق معروفة منذ العصور القديمة – الاحتكاك.
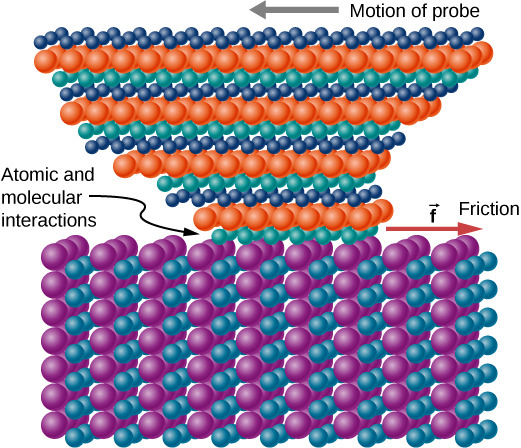
شكل 6.16: يتشوه طرف المسبار بشكل جانبي بفعل قوة الاحتكاك أثناء سحب المسبار عبر سطح ما. تعطي قياسات كيفية اختلاف القوة للمواد المختلفة رؤى أساسية حول الطبيعة الذرية للاحتكاك.
تعليم تفاعلي
صِف نموذجًا للاحتكاك على المستوى الجزيئي. صِف المادة من حيث الحركة الجزيئية. يجب أن يشتمل الوصف على رسوم بيانية لدعم الوصف؛ كيف تؤثر درجة الحرارة على الصورة؛ ما هي الاختلافات والتشابهات بين حركة الجسيمات الصلبة والسائلة والغازية؛ وكيف يرتبط حجم وسرعة جزيئات الغاز بالأشياء اليومية.
أمثلة وتطبيقات على الاحتكاك
مثال 6.12: كتل منزلقة
الكتلتان في الشكل 6.17 متصلتان ببعضهما البعض بواسطة خيط عديم الكتلة ملفوف حول بكرة عديمة الاحتكاك. عندما يتم سحب الكتلة السفلية التي تزن 4.00 كجم إلى اليسار بواسطة القوة الثابتة P⃗تنزلق الكتلة العلوية 2.00 كجم عبرها إلى اليمين. أوجد مقدار القوة اللازمة لتحريك الكتل بسرعة ثابتة. افترض أن معامل الاحتكاك الحركي بين جميع الأسطح يساوي 0.400.
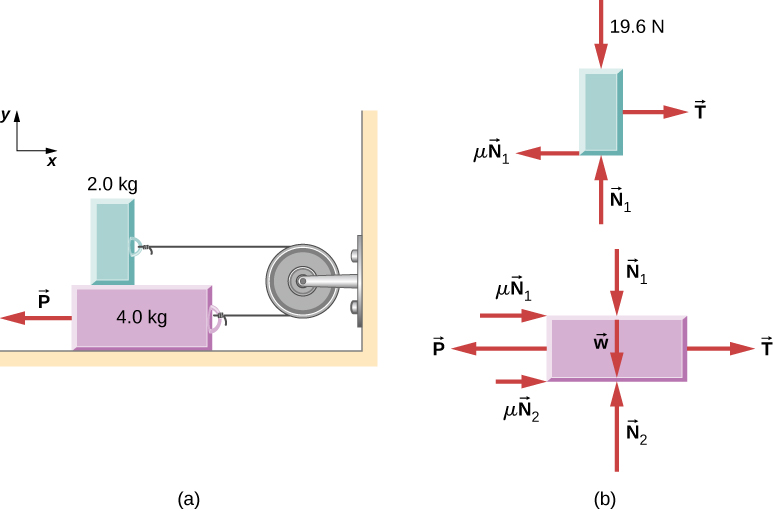
شكل 6.17: (أ) تتحرك كل كتلة بسرعة ثابتة. (ب) مخططات الجسم الحر للكتل.
استراتيجية الحل
نقوم بتحليل حركات الكتلتين بشكل منفصل. تتعرض الكتلة العلوية لقوة اتصال تمارسها الكتلة السفلية. مكونات هذه القوة هي القوة الطبيعية N1 وقوة الاحتكاك – 4.00 N1.
القوى الأخرى في الكتلة العلوية هي التوتر (الشد) في الخيط T ووزن الكتلة العلوية نفسها، 19.6 نيوتن. تتعرض الكتلة السفلية لقوى التلامس بسبب الكتلة العلوية وبسبب الأرضية. قوة التلامس الأولى لها مكونات −N1, 0.400N1 وهي مجرد قوى رد فعل لقوى التلامس التي تمارسها الكتلة السفلية على الكتلة العلوية. مكونات قوة التلامس للأرضية
N2, 0.400N2. والقوى الأخرى في هذه الكتلة هي −P، التوترTi والوزن -39.2 نيوتن.
الحل
نظرًا لأن الكتلة العلوية تتحرك أفقيًا إلى اليمين بسرعة ثابتة، فإن تسارعها يساوي صفرًا في كلا الاتجاهين الأفقي والرأسي. من قانون نيوتن الثاني يكون لدينا:
∑ Fx = m1 ax
T − 0.400 N1 = 0
وكذلك:
∑ Fy = m1 ay
N1 − 19.6 N = 0
بحل المعادلتين نحصل على القيم المجهولة:
N1 = 19.6 N, T = 0.40 N1 = 7.84 N
الكتلة السفلية أيضًا لا تتسارع، لذا فإن تطبيق قانون نيوتن الثاني على هذه الكتلة يعطينا:
∑ Fx = m2 ax
T – P + 0.400 N1+ 0.400N2 = 0
وكذلك:
∑ Fy = m2 ay
N2 − 39.2N − N1 = 0
تم إيجاد قيم T وN1 من المجموعة الأولى من المعادلات. عندما يتم استبدال هذه القيم في المجموعة الثانية من المعادلات، يمكننا معرفة قيم كل من P وN2 كما يلي:
N2 = 58.8 N
P = 39.2 N
الدلالة
غالبًا ما يكون فهم الاتجاه الذي يتم فيه رسم قوة الاحتكاك أمرًا مزعجًا. لاحظ أن كل قوة احتكاك موضحة في الشكل 6.17 تعمل في الاتجاه المعاكس لحركة الكتلة المقابلة لها.
مثال 6.13: صندوق على شاحنة متسارعة
صندوق يزن 50.0 كجم موضوع على ظهر الشاحنة كما هو موضح في الشكل 6.18. معاملات الاحتكاك بين الأسطح هي μk=0.3, μs=0.4.
أوجد قوة الاحتكاك المؤثرة على الصندوق عندما تتسارع الشاحنة للأمام بالنسبة للأرض عند (أ) 2.00 م / ث2، (ب) 5.00 م / ث2.
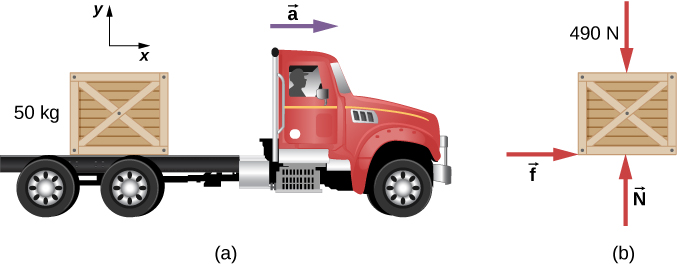
استراتيجية الحل
القوى الموجودة على الصندوق هي وزنه والقوى الطبيعية والاحتكاكية الناتجة عن ملامسة الصندوق للشاحنة. نبدأ بافتراض أن الصندوق لا ينزلق. في هذه الحالة، قوة الاحتكاك الساكن Fs تعمل على الصندوق. علاوة على ذلك، يكون تسارع الصندوق والشاحنة متساويان.
الحل
ينتج عن تطبيق قانون نيوتن الثاني على الصندوق، باستخدام الإطار المرجعي المرتبط بالأرض:
∑ Fx = m ax
fs = (50.0 kg)(2.00 m/s2) = 1.00 × 102 N
وكذلك:
∑ Fy = m ay
N – 4.9 ×102 N = (50.0 kg)(0)
N = 4.9 ×102 N
يمكننا الآن التحقق من صحة افتراض عدم الانزلاق. أقصى قيمة لقوة الاحتكاك الساكن هي:
μs N = (0.400)(4.90×102N) = 196 N
في حين أن القوة الفعلية للاحتكاك الساكن التي تعمل عندما تتسارع الشاحنة للأمام عند تسارع قيمته 2 م/ث2، هو فقط 1 × 10 2 نيوتن. وبالتالي، فإن افتراض عدم الانزلاق صحيح.
ب. إذا كان الصندوق سيتحرك مع الشاحنة عندما تتسارع بتسارع قيمته 5 م/ث2، فيجب أن تكون قوة الاحتكاك الساكن تساوي:
fs = m ax = (50.0kg)(5.00m/s2) = 250 N
نظرًا لأن هذا يتجاوز الحد الأقصى البالغ 196 نيوتن، يجب أن ينزلق الصندوق.
وبالتالي فإن قوة الاحتكاك تصبح حركية وهي تساوي:
fk = μk N = (0.300)(4.90 × 102N) = 147 N
والآن يمكن إيجاد التسارع الأفقي للصندوق بالنسبة إلى الأرض كما يلي:
∑ Fx = m ax
147 N = (50.0 kg) ax
ax = 2.94m/s2
الدلالة
بالنسبة إلى الأرض، تتسارع الشاحنة للأمام عند 5 متر/ث2، والصندوق يتسارع إلى الأمام عند 2.94 متر/ث2. ومن ثم فإن الصندوق ينزلق للخلف بالنسبة لظهر الشاحنة مع تسارع قيمته 2.94 متر/ث2 – 5 متر/ث2 = – 2.06 متر/ث2.
مثال 6.14: التزلج على الجليد
في وقت سابق، قمنا بتحليل حالة متزلج علة منحدر يتحرك بسرعة ثابتة لتحديد معامل الاحتكاك الحركي. لنقم الآن بتحليل مشابه لتحديد التسارع. ينزلق المتزلج على الجليد كما في الشكل 6.19 على منحدر يميل بزاوية مقدارها θ =13° درجة مع الأفقي. معامل الاحتكاك الحركي بين اللوح والثلج هو μk = 0.2. ما هو تسارع المتزلج على الجليد؟
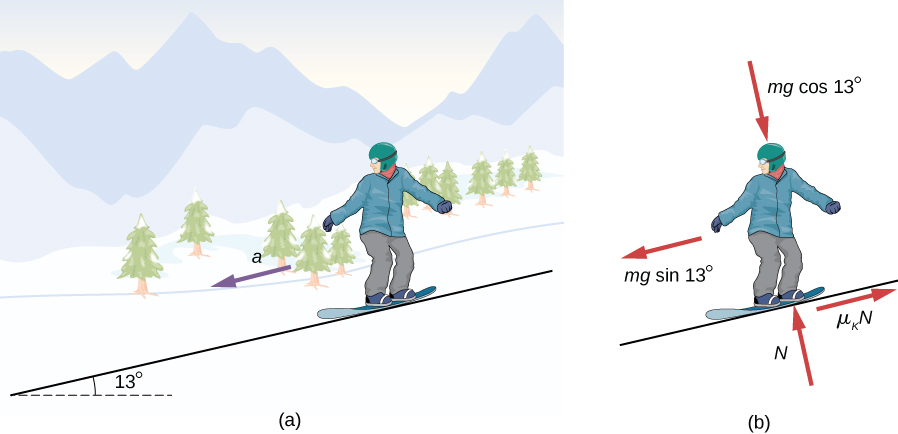
شكل 6.19: (أ) تنزلق متزلجة على الجليد على منحدر مائل بزاوية 13 درجة على الأفقي. (ب) مخطط الجسم الحر للمتزلجة على الجليد
استراتيجية الحل
القوى المؤثرة على المتزلجة على الجليد هي وزنها وقوة التلامس للمنحدر، والذي له مكون عمودي على المنحدر ومكون على طول المنحدر (قوة الاحتكاك الحركي). نظرًا لأنها تتحرك على طول المنحدر، فإن الإطار المرجعي الأكثر ملاءمة لتحليل حركتها هو الإطار الذي يحتوي على المحور x على طول المحور والمحور y العمودي على المنحدر. في هذا الإطار، تقع كل من القوى الطبيعية وقوى الاحتكاك على طول محاور الإحداثيات. ومكونات الوزن هي:
m g sinθ على طول المنحدر وmgcosθ عموديًا على المنحدر (بزاوية قائمة). والتسارع (العجلة) الوحيد هو على طول المحور السيني (أي أن ay=0).
الحل
يمكننا الآن تطبيق قانون نيوتن الثاني على المتزلج على الجليد:
∑ Fx = m ax
mg sin θ − μk N = max
وكذلك:
∑ Fy = m ay
N – mg cos θ = m (0)
من المعادلة الثانية، لدينا N = mg cos θ، بالتعويض عن هذه القيمة في المعادلة الأولى نحصل على:
ax = g (sin θ – μk cos θ) = g (sin 13° − 0.20 cos 13°) = 0.29 m/s2
الدلالة
لاحظ من هذه المعادلة أنه إذا كانت الزاوية ثيتا θ صغيرة بما فيه الكفاية أو معامل الاحتكاك μk كبير بما فيه الكفاية، فإن التسارع ax يصبح بقيمة سالبة، أي أن المتزلج يبطئ.
تحقق من فهمك
المتزلج على الجليد يتحرك الآن أسفل منحدر يميل بزاوية 10.0° مع الأفقي. ما هو تسارع المتزلج على الجليد؟
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.