المحتويات
أقساط التأمين على الحياة
أقساط التأمين على الحياة – بالإنجليزية Life Insurance Premiums – هي أقساط يتم تسديدها إما دفعة واحدة فيطلق عليها القسط الوحيد Single premium، وإما على دفعات دورية طول مدة العقد – وعادة ما يكون الدفع سنويًا – فيطلق عليها الأقساط السنوية العادية Ordinary Annual premiums. وإما على دفعات سنوية خلال مدة أقل من مدة العقد فيطلق عليها أقساط سنوية محدودة أو Limited Annual premiums.
والأصل في أقساط تأمين الحياة أن تكون إما أقساط وحيدة أو أقساط سنوية، ولكن بالرغم من ذلك فإن هيئة التأمين في سبيل تسهيل عملية سداد الأقساط تقبل في بعض الأحيان تجزئة الأقساط السنوية إلى دفعات دورية تُدفع كل نصف سنة أو ربع سنة أو كل شهر حسب الأحوال. وفي نظير زيادة مصاريف التحصيل يقوم المؤمن بإضافة علاوة تجزئة إلى القسط السنوي قبل قسمته على عدد فترات أو مرات السداد خلال السنة الواحدة.
أقساط التأمين على الحياة المجزأة
تتراوح علاوة التجزئة في شركات التأمين عادة بين 2% من القسط السنوي و8% منه. فإذا كان المستأمن يطلب السداد شهريًا فتكون علاوة التجزئة 8%. أما إذا كان السداد كل ربع سنة فتكون العلاوة 4%. وإذا كان السداد نصف سنوي تكون العلاوة 2% مثلاً. فإذا فرض أن القسط السنوي لوثيقة تأمين ما هو مبلغ مئة جنيه. وكان علاوات التجزئة في شركة التأمين مثل ما سبق ذكره، فإن الأقساط الدورية تُحسب كالآتي:
القسط السنوي لوثيقة التأمين = 100 جنيه
علاوة التجزئة نصف السنوية = 100 × 2 ÷ 100 = 2 جنيه
القسط النصف سنوي = (100 + 2) ÷ 2 = 51 جنيه
علاوة التجزئة ربع السنوية = 100 × 4 ÷ 100 = 4 جنيه
القسط النصف سنوي = (100 + 4) ÷ 4 = 26 جنيه
علاوة التجزئة الشهرية = 100 × 8 ÷ 100 = 8 جنيه
القسط النصف سنوي = (100 + 8) ÷ 12 = 9 جنيه
وعلى ذلك يمكن ترتيب أقساط وثيقة تأمين حياة معينة حسب حجم القسط المطلوب تصاعديًا كالاتي:
ترتيب أقساط التأمين على الحياة المجزأة تصاعديًا
- القسط الشهري العادي (أي الذي يدفع طول مدة العقد).
- القسط الربع سنوي العادي.
- والقسط النصف سنوي العادي.
- القسط المجزأ المحدود (أي الذي يسدد خلال مدة أقل من مدة العقد). مع ملاحظة أن قيمة القسط تتزايد بتناقص المدة التي تسدد خلالها الأقساط.
- القسط السنوي العادي.
- والقسط السنوي المحدود، مع ملاحظة أن قيمة القسط تتزايد بتناقص المدة التي تسدد خلالها الأقساط.
- القسط الوحيد.
ويقوم المستأمن باختيار الطريقة التي تناسبه للاتفاق على دفع القسط حسب مقدرته المالية. وبالرغم من عمليات تسهيل دفع الأقساط هذه، إلا أن القسط الشهري العادي – وهو أسهل الأقساط جميعها من ناحية الدفع – يحقق في نهاية مدة التعاقد تكلفة أكثر من أي طريقة سداد أخرى. ذلك نظرًا لاستخدام معدل اعلى لحساب علاوة التجزئة عند حساب القسط.
مثال تطبيقي
فمن المثال الوارد أعلاه يتضح أن مجموع الأقساط المسددة في كل حالة – بفرض بقاء المستأمن على قيد الحياة إلى نهاية مدة العقد (ولتكن عشر سنوات) – تكون كالآتي:
1. مجموع الأقساط المسددة في حالة القسط الشهري العادي
= قيمة القسط الشهري × عدد أشهر مدة الدفع
= 9 × (10 × 12) = 1080 جنيه
2. مجموع الأقساط المسددة في حالة القسط الربع سنوي العادي
= قيمة القسط الربع سنوي × عدد مرات الدفع
= 26 × (10 × 4) = 1040
3. مجموع الأقساط المسددة في حالة القسط النصف سنوي العادي
= 51 × (10 × 2) = 1020
4. مجموع الأقساط المسددة في حالة القسط السنوي العادي
= 100 × 10 = 1000
وبالمثل لو كنا قد حسبنا رياضيًا قيمة القسط السنوي المحدود والأقساط الدورية التي يمكن حسابها على أساسه وكذلك القسط الوحيد للوثيقة لاتضح لنا صحة الترتيب السابق وضعه بالنسبة لتدرج الأقساط حسب قيمتها من ناحية وحسب مجموعها من ناحية أخرى.
ملاحظة على حساب أقساط التأمين على الحياة المجزأة
ومن الملاحظ أن حساب القسط المجزأ بالطريقة السابق الإشارة إليها يقوم على أساس رياضي غير سليم. فعند حساب الأقساط هذه لا يؤخذ في الحسبان احتمال وفاة المستأمن خلال العام، وبذلك يكون قد سدد عددًا من أقساط العام الشهرية ولم يسدد الباقي. على عكس ما يحدث في حالة الأقساط السنوية إذ أنها تسدد في أول كل عام فلا يضيع على المؤمن أجزاء من القسط خلال العام. وعلى ذلك جرى العرف في سوق التأمين على أنه إذا حدثت الوفاة قبل أن يكون المستأمن قد قام بسداد أجزاء الأقساط السنوية فإن المؤمن يخصم تلك الأجزاء عن باقي أجزاء السنة من مبلغ التأمين ويسدد للورثة الباقي.
ففي المثال المذكور سابقًا والذي وجد فيه أن قيمة القسط الشهري تسع جنيهات، نفرض أن مبلغ التأمين كان ألف جنيه يستحق للورثة في حالة وفاة المؤمن على حياته. ونفرض أن الوفاة قد حدثت خلال شهر أغسطس. وبذلك يكون المستأمن قد سدد أقساط ثمانية شهور فقط من السنة التي حدثت فيها الوفاة. وتكون هناك أقساط أربعة شهور من السنة واجبة الخصم من مبلغ التأمين. ويترتب على ذلك أن يقوم المؤمن بسداد مبلغ الألف جنيه مخصومة منها مبلغ ستة وثلاثون جنيها. أي يقوم بدفع مبلغ 964 جنيه فقط للورثة.
مراحل حساب أقساط التأمين على الحياة
يحسب قسط تأمين الحياة – سواء كان القسط الوحيد أو القسط السنوي – على مرحلتين. الأولى خاصة بحساب القسط الصافي Net Premium. والثانية خاصة بحساب القسط التجاري Gross Premium.
ويُقصد بالقسط الصافي ما يخص المستأمن من ذلك المبلغ الذي يتسلمه المؤمن من جميع المستأمنين لكي يغطى دفع مبالغ التأمين المطلوبة حسب التعاقد. ويعتمد حساب القسط الصافي هذا في المكان الأول على احتمالات الحياة والوفاة المستعملة والتي تعتمد بدورها على جدول الحياة المستعمل.
وبالنسبة إلى أقساط التأمين تتجمع لدى المؤمن بمبالغ ضخمة ولمدد قد تطول أو تقصر حسب طول مدة التعاقد، فإن هذه الأقساط المتجمعة لا بد من استثمارها حتى لا تبقى عاطلة حتى ميعاد استحقاق مبالغ التأمين. فكلما كان الاستثمار مباشرًا وكلما ارتفع معدل عائد الاستثمار كلما نقصت قيمة القسط المطلوب دفعه. وقد جرت العادة على أن يكون معدل الاستثمار الذي يُحسب على أساسه القسط الصافي بين 2% و3.5% سنويًا.
وعلى ذلك يكون هناك عاملان أساسيان يحسب على أساسهما القسط الصافي لوثائق التأمين وهما احتمالات الحياة والوفاة من ناحية ومعدل استثمار الأقساط المحصلة من ناحية أخرى.
ويُقصد بالقسط التجاري ذلك المبلغ الذي يتسلمه المؤمن من كل من المستأمنين لكى يغطى دفع مبالغ التأمين المطلوبة حسب التعاقد، ولكي يغطي أيضًا المصاريف الإدارية الثابتة منها والمتغيرة. ولكي يبقى له أخيرًا جزء فائض كربح نظير قيامه بعملية تنظيم مشروع التأمين. ويُطلق على المصاريف والربح المضافين إلى القسط الصافي أعباء القسط أو Premium Load. وعلى ذلك فإن العوامل الأساسية التي يحسب على أساسها القسط التجاري تنحصر في القسط الصافي، ومعدلات المصروفات، ومعدل ربح التنظيم.
عوامل حساب القسط التجاري
ويمكن تلخيص النتائج السابق الحصول عليها في أن القسط التجاري لعقود التأمين على الحياة يعتمد في حسابه ويتأثر بعوامل أساسية هي:
جدول الحياة المستعمل
إذ أن على أساسه تحسب احتمالات الحياة واحتمالات الوفاة التي تستعمل في حساب القسط. فإذا كانت الوثيقة متعلقة بخطر الحياة، وإذا كانت احتمالات الحياة في الجدول المستعمل محسوبة على أساس متحفظ (أي أكبر من غيرها المحسوبة على أساس جدول آخر)، فإن القسط المحسوب يكون أكبر من مثيله المحسوب على أساس الجدول غير المتحفظ.
أعباء القسط
مع ملاحظة أنه كلما انخفضت هذه الأعباء كلما انخفض القسط، وكلما زادت ارتفع القسط.
معدل فائدة الاستثمار المستعمل
مع ملاحظة أنه كلما انخفض المعدل كلما زادت قيمة القسط، وكلما ارتفع كلما قلت قيمة القسط.
جداول الحياة
جداول الحياة أو Life Tables المستعملة في حساب أقساط التأمين في الإحصائيات التي تجمعها شركات التأمين من واقع الخبرة العملية لها وللشركات الأخرى والتي تبوب في جدول يبين أساسًا عدد الأشخاص المؤمن على حياتهم في تمام سن معين وعدد المتوفين منهم خلال كل عام. ويطلق البعض على جداول الحياة في بعض الأحيان جداول الوفاة Mortality Tables، ولا فرق إطلاقًا بين المسميين.
وجداول الحياة أو جداول الوفاة تصمم بحيث تبين عدد الأحياء وعدد الوفيات في كل من الأعمار المختلفة على أساس أنها تجربة حدثت لشركات التأمين في الماضي. ومن ثم فتتمكن هذه الشركات – على ضوء التجربة السابقة – من حساب الاحتمالات التجريبية المتوقعة بالنسبة لطالبي التأمين، والتي على ضوئها ممكن حساب أقساط التأمين بالنسبة لهم مقدمًا. وهذه الجداول تحتاج عادة لفترة خبرة طويلة تمكن الشركات خلالها من جمع البيانات اللازمة لتكوينها. ثم تقوم بإجراء عمليات رياضية خاصة يتم بعدها التوصل إلى عمل الجداول في صورتها النهائية والتي تظهر البيانات الرئيسية فيها في الأعمدة الآتية:
مكونات جداول الحياة
عمود السن
والذي بين الأعمار المختلفة التي تمت عليها التجربة وجمعت عنها المعلومات. ويمكن البداية بأي عمر كان، إلا أن جداول الحياة العادية تبدأ عادة بالعمر 10 وجداول حياة الأطفال تبدأ عادة من السن صفر، أي من يوم ولادتهم. وينتهي جدول الحياة أيًا كان بالعمر الذي يموت في نهايته باقي أفراد التجربة الموجودين على قيد الحياة. ويُطلق على هذا العمر الأخير سن نهاية الجدول أو Limiting Age.
عمود عدد الأحياء
والذي يبين عدد الأشخاص الموجودين على قيد الحياة في تمام الأعمار المختلفة. ويبدأ الجدول الخاص بالبالغين مثلاً بعدد الأحياء في تمام السن عشرة ويسمى هذا العدد أساس الجدول Radix. ولا بد أن يختار أساس الجدول عددًا كبيرًا يسمح بتطبيق قانون الأعداد الكبيرة، ولذلك فقد جرى العرف على أن يكون هذا العدد مئة ألف شخص أو أي عدد صفري آخر أكبر منه. ثم يسجل في هذا العمود أيضًا عدد الأحياء الباقين على قيد الحياة من الأساس السابق الإشارة إليه في الأعمار المختلفة. وينتهي الجدول عادة بعدد الأحياء في تمام سن نهاية الجدول والذين لا يبقى منهم أحد على قيد الحياة في نهاية تلك السنة.
عمود عدد الوفيات
والذي يبين فيه عدد المتوفين خلال كل سنة من سنوات الأعمار الموجودة بجدول الحياة. وهذا العدد يمكن الحصول عليه نظريًا بواسطة المشاهدة من التجربة. أما عمليًا فيحصل الرياضيون عليه عن طريق عمليات رياضية أو حسابية عن طريق المعلومات الموجودة بالأعمدة الأخرى من الجدول.
عمود احتمال الوفاة
والذي يبين احتمال الوفاة خلال سنة لكل عمر من الأعمار الموجودة في الخانة الأولى. وعمود احتمال الوفاة هذا هو الوحيد الذي يكون قد حسب على أساس خبرة شركات التأمين في الماضي بالنسبة لكل سنة من الأعمار المختلفة. وعلى ضوء معرفة الرياضيين لهذه الاحتمالات وبعد اختبارهم لعدد مناسب على أنه أساس الجدول يمكن تكوين أعمدة الجدول الأخرى سواء منها ما ذكر سابقًا أو أية أعمدة إضافية أخرى مثل عمود احتمال الحياة والذي يبين احتمال الحياة لمدة سنة لكل عمر من الأعمار الموجودة في الخانة الأولى.
تحديث جداول الحياة
وفي الدول التي تهتم شركات التأمين فيها بعمل جداول الحياة على أساس خبرة المؤمن على حياتهم فيها، فإنه يتحتم عليها إعادة النظر في هذه الجداول كل عشر سنوات تقريبًا. ذلك لأن الأحوال الصحية تتغير من حين إلى آخر بالنسبة لعوامل عدة منها تطور الطب والعلاج والأدرية مما يؤدي إلى تغيير احتمالات الحياة والوفاة التي تقاس من تلك الجداول. كذلك فإن اختلاف الظروف الاقتصادية والاجتماعية من بلد إلى آخر يحتم عمل جداول حياة خاصة بكل بلد تتناسب وهذه الظروف وما يترتب عليها من خبرة خاصة.
أمثلة لجداول الحياة
جدول الحياة المصري
جدول الحياة المصري الوحيد هو ذلك الذي تكون على أساس خبرة موظفي الحكومة المصرية الذين كانوا يخضعون لنظام المعاش الحكومي عن المدة من عام 1922 إلى عام 1928 والذي قام بعمله (مستر كريج) الخبير بوزارة المالية في ذلك الوقت. وقد حدثت بعض المحاولات الفردية لعمل جداول خبرة محدودة البيانات وتعتمد على اجتهادات شخصية بحته ولذلك لم تتمكن شركات التأمين المصرية من استخدامها. وقد قام أكثر من خبير من الخبراء الاكتواريين المصريين بعمل جداول حياة من واقع الإحصاء السكاني. وهذه بطبيعة الحال لا يمكن استخدامها في حساب أقساط التأمين لأنها لا تعتمد على خبرة شركات التأمين في الماضي.
جدول الحياة الإنجليزي
وفي إنجلترا ظهرت جداول عدة أولها المجموعة التي ظهرت عام 1899 وأطلق عليها جداول الخبراء الاكتوارييين. ومجموعة جداول رؤساء التأمين التي أنشئت على أساس خبرة ثلاثين سنة من عام 1863 إلى عام 1893. ومجموعة جداول خبراء التأمين عن أصحاب دفعات المعاش والتي نشرت عام 1924. وكذلك مجموعة جداول التأمين على أصحاب المعاش الحكوميين والتي عملت على أساس الخبرة بين عام 1900 وعام 1920. وأخيرًا الجدول الذي أنشئ على أساس الخبرة بين عام 1929 وعام 1934 والذي نشر عام 1934.
جدول الحياة الأمريكي
وفي أمريكا ظهرت عدة جداول حياة تعتمد على خبرة شركات التأمين الأمريكية أولها جدول الخبرة الأمريكية وظهر عام 1867. والجدول الأمريكي لثلاثين من رؤساء التأمين والذي أنشئ على أساس خبرة المدة من عام 1844 إلى عام 1874. والجدول الأمريكي للرجال والمكون على أساس خبرة من عام 1900 إلى عام 1915 والذي ظهر عام 1918. وجدول رؤساء التأمين الموحد العادي لعام 1941. وكذلك جدول أصحاب المعاشات للذكور لعام 1949. وجدول رؤساء التأمين الموحد العادي لعام 1958. وأخيرًا جدول رؤساء التأمين الموحد العادي لعام 198 والذي يطلق عليه 1968 CSO.
وفي مصر تقوم شركات التأمين المصرية باستعمال جداول حياة إنجليزية وفرنسية وأمريكية وسويسرية وغيرها مما لا يبين حقيقة الخبرة المصرية ولا يوضح صورتها على الوجه الحقيقي. ولكي تتلاءم جداول الحياة هذه مع معدلات الحياة والوفاة المصرية يعمد الخبراء الاكتواريون الذين يقومون بحساب الأقساط في هذه الشركات إلى إجراء تعديلات فيها حتى تتناسب مع الخبرة المصرية.
دراسة مقارنه لبعض جداول الحياة
يبين الجدول التالي مدى اختلاف الجداول المتعددة في حساب احتمالات الوفاة السنوية لعدة أعمار. مما يترتب عليه ضرورة اختيار الجدول المناسب للمكان والزمان المناسبين:
جدول يبين اختلاف الجداول المتعددة في حساب احتمالات الوفاة:
| الجدول | احتمالات الوفاة لمدة سنة | |||
| للسن 20 | للسن 30 | وللسن 40 | للسن 50 | |
| جدول المعاش المصري (1922-1928) | 0.00207 | 0.00317 | 0.00604 | 0.01357 |
| جدول الخبرة الأمريكي (1843-1858) | 0.00777 | 0.00842 | 0.00979 | 0.01378 |
| الجدول الموحد الأمريكي لعام 1941 | 0.00243 | 0.00356 | 0.00618 | 0.01222 |
| الجدول الموحد الأمريكي لعام 1958 | 0.00179 | 0.00212 | 0.00353 | 0.00832 |
| جدول الخبرة الإنجليزي (1924-1929) | 0.00225 | 0.00241 | 0.00388 | 0.00764 |
| جدول الخبرة الفرنسي لعام 1882 | 0.00690 | 0.00698 | 0.00975 | 0.01638 |
ملاحظات على جداول الحياة
وبدراسة احتمالات الوفاة الواردة في الجدول السابق تتضح عدة ملاحظات هامة يمكن تلخيصها فيما يلي:
- بمقارنة جداول الخبرة الأمريكية الثلاثة يلاحظ أن احتمالات الوفاة بالنسبة للمستأمنين الأمريكيين في تحسن مستمر من فترة لأخرى. فأعلى احتمالات وفاة موجودة في جدول الخبرة الأمريكي الأول (1843 – 1858) وأقلها موجودة في جدول الخبرة الأمريكي الأخير لعام 1958. من هذا يتضح أن أسعار تأمينات الحياة في أمريكا انخفضت كثيرًا باستعمال جدول عام 1958 عما كانت عليه من قبل. ولهذا تحتم الحكومات التي تقوم بدور الإشراف والرقابة على هيئات التأمين ضرورة إعادة النظر في جداول الحياة كل فترة معينة. وتحتم جهات الإشراف الأمريكية عمل جدول خبرة جديد كل عشر سنوات.
- احتمالات الوفاة في جدول المعاش المصري (1922 – 1928) قريبة جدًا من مثيلاتها المناظرة لها في الجدول الموحد الأمريكي لعام 1941. مما يسمح باستعمال الجدول الأخير في حساب الأقساط في مصر. ولكنها بعيدة كل البعد عن تلك المناظرة لها في كل من جدول الخبرة الإنجليزي والفرنسي بالرغم من أنهما كثيرة الاستعمال في حساب الأقساط في مصر ولكن بعد إدخال تعديلات عليها.
- تختلف الاحتمالات المناظرة من بلد لآخر اختلافًا واضحًا مما يصعب معه استعمال جدول أمريكي في إنجلترا أو جدول إنجليزي في فرنسا. وذلك لاختلاف البيئة والحالة الاجتماعية والاقتصادية والتي تؤثر جميعها على أعمار الأشخاص. ولذلك يجب على الخبراء الرياضيين إجراء التعديلات اللازمة في الجدول الأجنبي قبل استخدامه محليًا.
الجدول الأمريكي الموحد لعام 1958
يعتبر جدول رؤساء التأمين الموحد العادي الأمريكي لعام 1958 Commissioners 1958 Standard Ordinary – أو ما يطلق عليه اختصارًا 1958 CSO – من أكثر الجداول انتشارًا واستعمالاً في الوقت الحاضر. خاصة وأنه من أكثر الجداول تساهلاً في حساب القسط بالنسبة لطالب التأمين. هذا بالإضافة إلى أنه يستخدم إجباريًا في جميع أنحاء الولايات المتحدة الأمريكية، كما يستعمل اختياريًا في كندا وأمريكا الجنوبية. وبطبيعة الحال لعبت المنافسة بين شركات التأمين دورًا هامًا في انتشار استعمال هذا الجدول بدلاً من الجداول الأمريكية القديمة أو الإنجليزية والفرنسية سواء في المستعمرات والبلاد الأجنبية أو داخل بلادها. وقد قام رؤساء التأمين في الولايات الأمريكية بعمل جدول حياة جديد آخر عام 1968 وقد بدأ تطبيقه في نهاية عام 1971.
وحيث أننا في حاجة ماسة إلى أرقام أي جدول من جداول الحياة لاستخدامها في حساب أقساط وثائق تأمينات الحياة المختلفة، فإننا نورد في الشكل التالي الجدول الأمريكي الموحد لعام 1958 المعمول عن أساس Radix قدرة عشرة ملايين شخص في تمام السن صفر والذي ينتهي في السن التاسعة والتسعين.
استخدام الجدول في حساب القسط الوحيد الصافي
يقصد بالقسط الصافي Net Single Premium ذلك القسط الذي يُدفع مرة واحدة عند التعاقد ويكون كافيًا لسداد نصيب المستأمن في المطالبات التي تقع على المؤمن خلال مدة التعاقد وبدون أن يضاف إليه أية مصروفات أو أرباح. وعلى ذلك فإن القسط الوحيد الصافي لأية وثيقة من وثائق تأمينات الحياة يقع مساويًا للقيمة الحالية للطالبات المتوقعة نتيجة سريان هذه الوثيقة محسوبة على أساس جدول حياة معين ومعدل فائدة متفق عليه.
فإذا فرض وإن كان لدينا ألف شخص في سن معين طلبوا التأمين على حياتهم بمبلغ ألف جنيه لكل منهم لمدة خمس سنوات. وأن عشرة منهم يتوقع وفاتهم في نهاية السنة الأولى من مدة التأمين. وأحد عشر في نهاية السنة الثانية، واثني عشر في نهاية السنة الثالثة. وثلاثة عشر في نهاية السنة الرابعة. وأربعة عشر في نهاية السنة الخامسة. فإن القسط الوحيد الصافي يحسب كالآتي:
مجموع المطالبات المتوقعة في نهاية السنة س = عدد وفيات نهاية السنة س × مبلغ تأمين الوثيقة الواحدة
وبتطبيق هذه المعادلة على كل السنوات، نحصل على التالي:
حساب مجموع المطالبات لكل سنة
مجموع المطالبات المتوقعة في نهاية السنة الأولى = عدد وفيات نهاية السنة × مبلغ تأمين الوثيقة الواحدة
= 10 × 1000 = 10000 جنيه
القيمة الحالية لمطالبات نهاية السنة الأولى في تاريخ التعاقد = مجموع المطالبات × القيمة الحالية للجنيه الواحد عن سنة بمعدل فائدة 2% مثلاً
= 10000 × القيمة الحالية للجنيه بمعدل 2%
= 10000 × ح بمعدل 2%
أي أنها:
= 10000 × 0.98039 = 9803.900 جنيه
وبالمثل:
مجموع مطالبات نهاية السنة الثانية = 11 × 1000 = 11000
القيمة الحالية لمطالبات نهاية السنة الثانية في تاريخ التعاقد = 11000 × ح 2 بمعدل 2%
= 11000 × 0.96117 = 10572.87 جنيه.
مجموع مطالبات نهاية السنة الثالثة = 12 × 1000 = 12000
القيمة الحالية لمطالبات نهاية السنة الثالثة في تاريخ التعاقد = 12000 × ح 3 بمعدل 2%
= 12000 × 0.0.94222 = 1307.84جنيه.
مجموع مطالبات نهاية السنة الرابعة = 13 × 1000 = 13000
القيمة الحالية لمطالبات نهاية السنة الرابعة في تاريخ التعاقد = 13000 × ح 4 بمعدل 2%
= 13000 × 0.92385= 12010.05جنيه.
مجموع مطالبات نهاية السنة الخامسة = 14 × 1000 = 14000
القيمة الحالية لمطالبات نهاية السنة الخامسة في تاريخ التعاقد = 14000 × ح 5 بمعدل 2%
= 14000 ×0.90573 = 12680.22 جنيه.
صور الجدول الأمريكي الموحد لعام 1958
صفحة 305 – (أ)
صفحة 306 (ب)
حساب مجموع القيم الحالية للمطالبات
مجموع القيم الحالية للمطالبات المتوقعة خلال مدة الوثيقة
= 9803.90 + 10572.87 + 11307.84 + 12020.05 + 12680.22 = 56274.88 جنيه.
ما يخص كل واحد من المستأمنين في هذه المطالبات (أي القسط الوحيد الصافي)
= مجموع القيم الحالية للمطالبات ÷ عدد المؤمن على حياتهم عند التعاقد
= 56374.88 ÷ 1000 = 56.377 جنيه.
خطوات حساب القسط الوحيد الصافي
يمكن تحديد الخطوات التي تتبع في حساب القسط الوحيد الصافي لوثيقة تأمين الحياة على ضوء المثال السابق كما يلي:
1. تحديد نوع المطالبات المتوقعة
فيجب معرفة ما إذا كانت الوثيقة تنص على الدفع في حالة الحياة مثلما يحدث في حالة الوقفية البحتة ودفعات الحياة أو في حالة الوفاة مثلما يحدث في حالة التأمين مدى الحياة والمؤقت. أو في حالة الحياة والوفاة معًا مثلما يحدث في حالة التأمين المختلط.
2. تحديد ميعاد دفع المطالبات المتوقعة
إذ أنه في بعض الوثائق تسدد مبالغ التأمين في أول كل سنة مثل حالة دفعات الحياة الفردية. وفي البعض الآخر تسدد المبالغ في آخر كل سنة مثل حالة دفعات الحياة العادية. أما مطالبات وثائق التأمين المؤقت ومدى الحياة وما شابهها فبالرغم من أنها تدفع لورثة المؤمن على حياتهم بمجرد وفاتهم وخلال العام، إلا أن الخبراء الرياضيين يفترضون دفع هذه المطالبات في نهاية السنة التي تحدث خلالها الوفاة حتى يسهل عليهم حساب المدة بالسنوات الكاملة وتسهل عملية حساب القسط. ويفيد تحديد ميعاد دفع الطالبات في تحديد المدة التي على أساسها تحسب القيم الحالية لهذه المطالبات في تاريخ التعاقد.
3. تحديد عدد الأشخاص المؤمن على حياتهم
إذ أن هذا العدد يتوقف عليه عوامل عدة تؤثر في حساب القسط الوحيد الذي يتحمله كل واحد منهم. وقد سبق أن أشرنا في أكثر من مكان إلى أنه يجب أن يكون مثل هذا العدد كبيرًا حتى يمكن عمل التوقعات بدقة تامة خاصة بالنسبة لعدد المطالبات السنوية لأولئك الذين يحل عليهم الدور من هذا العدد. وقد جرت العادة عند حساب القسط على افتراض أن عدد الأشخاص الموجودين في عمود عدد الأحياء أمام السن المقابل هو عدد الأشخاص الذين يريدون التأمين على حياتهم مثلهم مثل الشخص طالب التأمين. أي أن القسط يحسب على أساس قانون الأعداد الكبيرة وبفرض أن جميع الأشخاص الذين في سن الشخص طالب التأمين سوف يقومون بشراء التأمين هم كذلك.
ففي حالة حساب قسط وثيقة تأمين مؤقت لشخص في تمام السن ثلاثين، وباستعمال الجدول الأمريكي الموحد لعام 1958 الوارد في الشكل أعلاه، نفترض أن عدد الأشخاص الذين يشتركون في عمل مثل هذه الوثيقة هم 9480358 شخصًا، ولا يعني هذا أن شركة التأمين لا بد وأن تصل إلى هذا الرقم قبل أن تبدأ عملها، ولكن هذا يعني أن حساب القسط مقدمًا يكون دقيقًا إلى أبعد الحدود إذا ما حسب على أساس أعداد كبيرة وكذا عملت التوقعات الخاصة بالطالبات على أساس الأعداد الكبيرة أيضًا حتى يكون التنبؤ أكثر دقة.
أما بالنسبة لعدد وثائق التأمين التي تتمكن الشركة من إصدارها فهذا يرجع أولاً وأخيرًا إلى نشاط رجال البيع فيها. وكلما زاد عدد الوثائق المُصدرة كلما حققت الشركة ما تصبو إليه من الوصول إلى عددًا أمثل يعتبر من الأعداد الكبيرة المتاحة لها.
4. تحديد الأعمار التي تغطيها وثيقة التأمين ومن ثم مدة الوثيقة نفسها
وهذه المدة وتلك الأعمار تعاون في تحديد عدد المطالبات وتاريخ دفعها.
5. تحديد عدد المطالبات المتوقعة سنويًا
وعادة ما يتم ذاك من واقع جدول الحياة المستعمل ومن أي من عمودي عدد الأحياء أو عدد الوفيات حسب نوع الوثيقة ونوع المطالبة. فإذا كنا قد أخذنا عدد المتعاقدين على التأمين من عمود عدد الأحياء بالجدول أمام السن المماثل لسن المتعاقد وهو سن الثلاثين مثلاً، وأن الوثيقة التي يراد حساب قسطها هي وثيقة وقفية بحتة لسن الخمسين، فإن عدد المطالبات المتوقعة تحدد بعدد الأشخاص الذي يصلون أحياء إلى تمام السن خمسين، أي 8762306 حسب البيانات الواردة في الجدول الأمريكي الموحد لعام 1958، أما إذا كانت الوثيقة متعلقة بتأمين مؤقت لمدة عشرين سنة، فإن عدد المطالبات السنوية المتوقعة يتحدد بعدد الوفيات من الجدول المذكور خلال المدة من السن ثلاثين إلى السن خمسين.
ففي نهاية السنة الأولى من سنة الوثيقة يكون عدد المطالبات 20193 مطالبة، وفي نهاية السنة الثانية يكون عددها 20718 مطالبة، وفي نهاية السنة الثالثة يكون عددها 31239 مطالبة، وهكذا إلى أن يكون عددها في نهاية السنة الأخيرة من سنوات الوثيقة 67104 مطالبة وذلك خلال عام السن من 49 إلى 50.
6. تحديد مجموع المطالبات السنوية
وذلك عن طريق ضرب عدد المطالبات المتوقعة سنويًا في قيمة المطالبة الواحدة والتي هي عبارة عن مبلغ التأمين في الوثيقة.
7. تحديد القيمة الحالية للجنيه
تحديد القيمة الحالية للجنيه عن سنوات المطالبات المتوقعة على أساس معدل الفائدة الذي تستخدمه الشركة في حساب الأقساط. ويجب أن يلاحظ في هذه الخطوة تاريخ سداد المطالبات، فإن هذا التاريخ سوف يحدد المدة التي على أساسها تحسب القيمة الحالية للجنيه.
ففي حالة وثيقة الوقفية البحتة لمدة عشرين سنة فإن القيمة الحالية للجنيه تحسب عن عشرين سنة مرة واحدة فقط إذ أن المطالبات المتوقعة سوف تحدث من أولئك الأشخاص الذين يبقون على قيد الحياة إلى نهاية مدة التعاقد وهي عشرين سنة. أما في حالة وثيقة التأمين المؤقت لمدة عشرين سنة فإن القيمة الحالية للجنية تحسب عن سنة وسنتين وثلاث سنوات وهكذا إلى أن تصل إلى آخر مطالبة متوقعة وهي تلك التي تستحق في آخر سنة من سنوات الوثيقة ومدتها عشرون سنة.
وهذه القيم الحالية للجنيه تستخرج من جداول الفائدة المركبة حسب معدل الفائدة المستعمل في شركة التأمين.
8. تحديد القيمة الحالية للمطالبات السنوية المتوقعة
وذلك بضرب مجموعة المطالبات السنوية في القيمة الحالية للجنيه عن المدة التي في نهايتها تدفع المطالبة السنوية.
9. تحديد القيمة الحالية للمطالبات المستقبلة المتوقعة إجمالاً
وذلك بجمع القيم الحالية للمطالبات السنوية المتوقعة السابق الحصول عليها في الخطوة السابقة.
10. تحديد القسط الوحيد الصافي
وذلك بقسمة القيمة الحالية للمطالبات المستقبلة المتوقعة إجمالاً والسابق الحصول عليها في الخطوة السابقة على عدد الأحياء في تمام السن الذي بدأت فيه عملية التأمين وذلك من واقع جدول الحياة المستعمل.
وفيما يلي شرحًا مفصلاً لكيفية تطبيق الخطوات السابق الإشارة إليها عند حساب وثائق التأمين في أهم صورها.
حساب القسط الوحيد الصافي لوثيقة تأمين الحياة المؤقت
عند حساب القسط الوحيد الصافي لوثيقة تأمين الحياة المؤقت، تتبع الخطوات السابقة بالاستعانة بجدول حياة – ولكن جدول الخبرة الأمريكي لعام 1958 – وبجدول فائدة مركبة لحساب القيم الحالية على أساس معدل فائدة معين وليكن 2% سنويًا.
فإذا أريد حساب القسط الوحيد الصافي لوثيقة تأمين حياة مؤقت بمبلغ ألف جنيه ولمدة عشر سنوات تصدر للأشخاص الذين في تمام السن ثلاثين مثلاً، فإنه يمكن وضع البيانات التي نحصل عليها نتيجة تطبيق الخطوات التسع الأولى في جدول كما هو مبين في الشكل أدناه.
ويلاحظ أن عدد المطالبات المتوقعة – وهو الخطوة الخامسة – هو عدد الوفيات في كل سنة من السنوات العشر التي يغطيها التأمين ابتداء من تمام السن 30 إلى تمام السن 40. أي أن عدد مطالبات السنة الأولى هم أولئك الذين ماتوا خلال السنة من تمام السن 30 إلى تمام السن 31. وعدد مطالبات السنة الأخيرة هم أولئك الذين توفوا بين تمام السن 39 إلى تمام السن 40.
كما يلاحظ أن كل مطالبة من هذه المطالبات سوف تكلف شركة التأمين مبلغ ألف جنيه. وعلى ضوء هذا حسبت مجموع المطالبات السنوية والتي تدفع أولها في نهاية السنة الأولى من مدة التأمين، وثانيها في نهاية السنة الثانية. وهكذا نجد أن آخرها تدفع في نهاية السنة العاشرة.
وبما أن مجموع المطالبات السنوية – وهي الخطوة السادسة – تدفع بمعرفة شركة التأمين إلى الورثة في نهاية كل سنة من السنوات العشر، فإنه يجب حساب قيمتها الحالية يوم التعاقد – أي في بداية العشر سنوات – لكي تقسم تلك القيم الحالية على المشتركين في التأمين، ولذلك استخرجت القيم الحالية للجنيه عن سنة وسنتين وهكذا إلى عشر سنوات على أساس معدل فائدة متفق عليه وهو 2% سنويًا. وهذه هي الخطوة السابعة.
شكل توضيحي
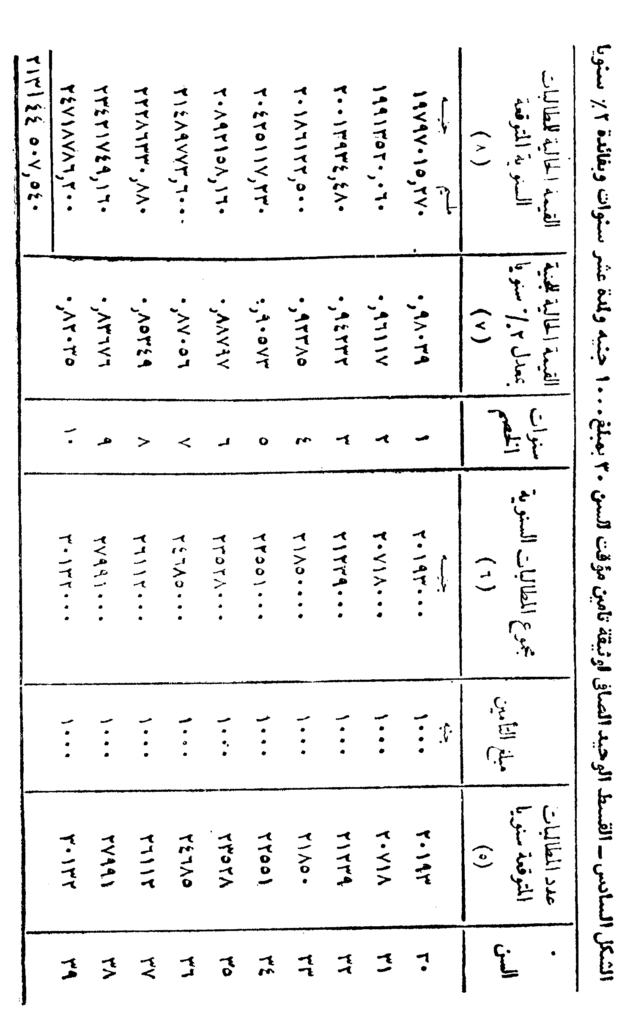
ثم حسبت القيمة الحالية للمطالبات السنوية المتوقعة بضرب كل مطالبة سنوية في القيمة الحالية للجنيه عن المدة المقابلة لها، وهي الخطوة الثامنة.
وبجمع العمود الأخيرة وجد أن القيمة الحالية للمطالبات المستقبلة التي تتوقعها شركة التأمين نظير هذا الاتفاق قد بلغت 213144507 جنيهات و540 مليمًا. وهذه هي الخطوة التاسعة.
أما الخطوة العاشرة والأخيرة، والخاصة بتحديد القسط الوحيد الصافي، فيمكن الوصول إليها بتوزيع هذه التكلفة الإجمالية للتعاقد على عدد الأحياء في تمام السن 30 والذين يفترض فيهم المشاركة في تحمل هذه التكلفة لتمتعهم بمزايا التأمين، وعددهم حسب جدول الحياة هو 9480358 شخصًا. وبذاك يكون القسط الوحيد الصافي لوثيقة تأمين الحياة المؤقت بمبلغ ألف جنيه لشخص في تمام السن 30 ولمدة عشر سنوات هو 22 جنيهًا و483 مليمًا.
أي أن مثل هذا الشخص يدفع لشركة التأمين هذا القسط مرة واحدة عند التعاقد وتضمن الشركة لورثته دفع مبلغ ألف جنيه، إذا توفي خلال عشر سنوات، أي خلال المدة من تمام السن 30 إلى تمام السن 40.
ويلاحظ أن القسط منخفض جدًا لسببين هامين: أولهما أن المؤمن على حياته ما زال صغير السن واحتمال وفاته منخفضًا. وثانيهما أن مدة التأمين – عشر سنوات – قصيرة وتنتهي قبل بلوغ الشخص سنًا كبيرة وهذا أيضًا يؤدي إلى أن يكون احتمال الوفاة خلال هذه المدة منخفضًا.
حساب القسط الوحيد الصافي لوثيقة تأمين مدى الحياة
عند حساب القسط الوحيد الصافي لتأمين مدى الحياة تتبع نفس الخطوات العشر السابق إتباعها في حساب القسط التأمين المؤقت وباستخدام جدول الحياة وجدول الفائدة المركبة أيضًا.
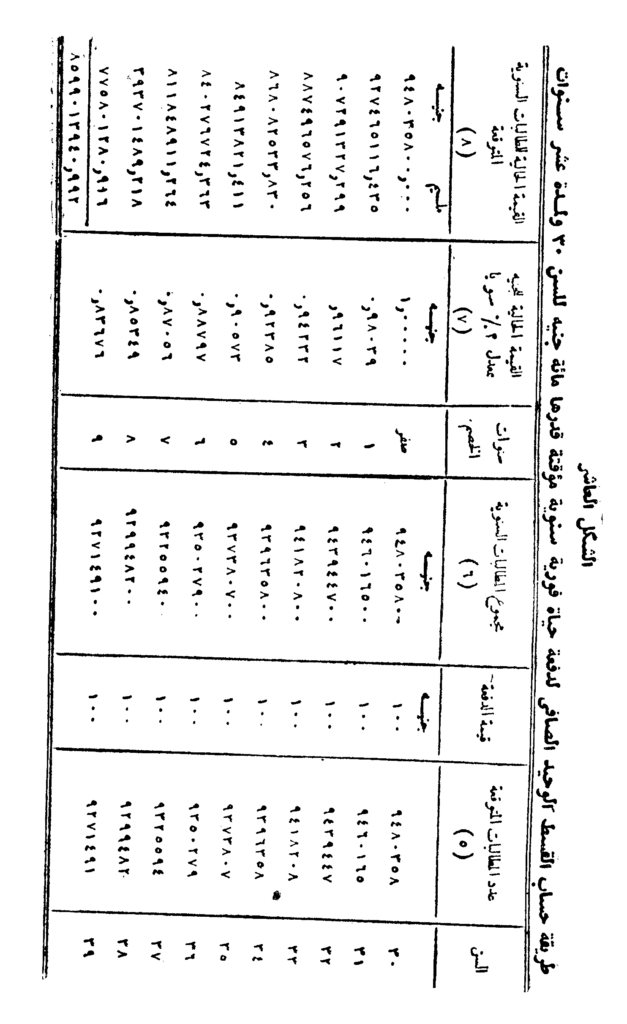
فاذا أريد حساب القسط الوحيد الصافي لتأمين مدى الحياة بمبلغ ألف جنيه وتصدر للأشخاص في سن التسعين، فإنه يمكن تطبيق الخطوات السابقة ووضع البيانات الخاصة بها في جدول كما هو مبين بالشكل التالي أدناه. هذا وقد اختير السن المتقدم هذا – سن التسعين – لحساب القسط حتى لا تزيد العمليات الحسابية الواجب إجراؤها، بالرغم من أن شركات التأمين تمتنع عادة عن إصدار وثائق تأمين مدى الحياة بعد السن 60 أو 65.
ويلاحظ أن عدد المطالبات المتوقعة هو عدد الوفيات كل سنة ابتداء من السنة الأولى للتعاقد وهو عدد وفيات السن من 90 إلى 91، حتى السنة الأخيرة أي السنة التي يموت فيها آخر الأحياء ولا يبقى بعدها أي شخص على قيد الحياة وهي السن من 99 إلى 100 حسب الجدول الأمريكي لعام 1958.
ملاحظة
وهنا يلاحظ أنه لو كنا قد أخترنا سنًا أصغر من 90 لكانت العمليات الحسابية قد امتدت لمدة طويلة يصعب الانتهاء منها في وقت محدود، ولكن وجود الآلات الحاسبة من ناحية والاختصارات الرياضية من ناحية أخرى يسهل مثل هذه العمليات كما يتبع في الطريقة المختصرة وبمساعدة جداول خاصة بالرموز الحسابية والتي يأتي ذكرها عادة في مراجع الرياضيات الاكتوارية.
ومجموع العمود الأخير من الجدول الموجود بالشكل السابق (أ) يمثل القيمة الحالية للمطالبات المستقبلة التي تتوقعها شركة التأمين من هذه العملية، وقد بلغت 160 مليمًا و436741410 جنيهات. والمبلغ الأخير يمثل تكلفة التأمين الإجمالية محسوبة على أساس قيمتها الحالية يوم الاتفاق. وبقسمة هذا الرقم على عدد الأحياء في تمام السن 90 وهو 468174 شخصًا – وهم أولئك الذين يشتركون في عملية التأمين والمستخرج عددهم من نفس الجدول المستعمل – ينتج القسط الوحيد الصافي لوثيقة تأمين مدى الحياة ويبلغ قيمته 861 مليمًا و932 جنيهًا.
ويلاحظ أن القسط مرتفع جدًا بالنسبة لمبلغ التأمين وهو ألف جنيه، وذلك راجع إلى أن التأمين قد عقد على حياة أشخاص في السن 90 ولمدى الحياة، وهذا ينتج عنه أن احتمال وفاة الشخص مرتفع جدًا ما يؤدي إلى ارتفاع قيمة القسط، وأن دفع مبلغ التأمين يحتمل أن يكون سريعًا أيضا مما يترتب عليه عدم إمكان استثمار الأموال المدفوعة كأقساط لمدة طويلة وهذا يؤدي بدوره إلى ارتفاع أكثر في قيمة القسط.
حساب القسط الوحيد الصافي لوثيقة تأمين مختلط
عند حساب القسط الوحيد الصافي لتأمين مختلط تتبع نفس الخطوات السابق الإشارة إليها وباستعمال جدول الحياة وجدول الفائدة المركبة أيضًا.
فإذا أريد حساب القسط الوحيد الصافي لتأمين مختلط بمبلغ ألف جنيه تصدر للأشخاص في سن الثلاثين لمدة عشر سنوات، فإنه يمكن تطبيق الخطوات السابقة ووضع البيانات الخاصة بها والناتجة عنها في جدول كما هو مبين بالشكل التالي أدناه.
ويلاحظ أن عدد المطالبات المتوقعة خلال مدة العشر سنوات تكون من نوعين مختلفين. النوع الأول هو عدد المطالبات الناشئة عن عدد المتوفين خلال هذه المدة تمامًا كما حدث بالنسبة للتأمين المؤقت. والنوع الثاني هو عدد المطالبات الناشئة عن عدد الأشخاص الباقين على قيد الحياة إلى أن يبلغوا تمام السن 40، إذ أن الوثيقة المختلطة تدفع لهؤلاء أيضًا مبلغ تأمينهم. كما يلاحظ أن المطالبات من النوع الثاني تدفع في نهاية مدة التأمين، أي في نهاية عشر سنوات في المثال الحالي.
ومجموع العمود الأخير من الجدول الموجود بالشكل السابق (ب) يمثل القيمة الحالية للمطالبات المستقبلة التي تتوقعها شركة التأمين من حملة هذه الوثيقة، وقد بلغت 190 مليمًا و7794293363 جنيهًا، وهذا يمثل تكلفة التأمين الإجمالية يوم الاتفاق. وبقسمة هذا الرقم على عدد الأحياء في تمام السن 30 وهو 9480358 شخصًا ينتج القسط الوحيد الصافي للوثيقة والذي يبلغ 152 مليمًا و832 جنيهًا.
ويلاحظ أن هذا القسط مرتفع خاصة وأن السن المحسوب على أساسه التأمين صغير. وهذا راجع إلى أن القسط هو مجموع قسطين لوثيقتي تأمين مختلفين هما تأمين مؤقت ووقفية بحتة. ومن المعلوم أن قسط التأمين المؤقت منخفض جدًا – وقد سبق حسابه لهذا السن ولنفس المدة ونفس مبلغ التأمين فوجد أنه 483 مليمًا و22 جنيهًا – وعلى ذلك فإن الجزء الأكبر من قسط الوثيقة المختلطة في المثال الحالي بالذات يدفع نظير الوقفية البحتة إذ أنه مرتفع دائمًا في حالة السن الصغير والمدة القصيرة.
حساب القسط الوحيد الصافي للوقفية البحتة
عند حساب القسط الوحيد الصافي لوقفية بحتة تتبع نفس الخطوات السابقة وتستعمل جداول الحياة وجداول الفائدة المركبة. وبالرغم من ذلك فإن العمليات الحسابية تكون دائمًا أقل كثيرًا من الحالات السابقة. ذلك لأن المطالبات المتوقعة تقع كلها في تاريخ واحد ولا تتكرر من سنة لأخرى. فالوقفية البحتة تشترط دفع مبلغ التأمين عند بلوغ الشخص السن الجديد، وعلى ذلك فإنها تدفع مرة واحدة لجميع الأشخاص.
فإذا أريد حساب القسط الوحيد الصافي لوقفية بحتة بمبلغ ألف جنيه تصدر للأشخاص في سن الأربعين ولمدة عشرين سنة، فإنه يلاحظ أن المطالبات سوف تتم مرة واحدة في نهاية مدة العشرين سنة. وبالنسبة لأولئك الذين يبقون على قيد الحياة حتى تمام السن 60. وعلى ذلك يكون عدد المطالبات هو عدد الأشخاص الذين يبلغون هذا السن وهو 7698698 شخصًا. وبما أن مبلغ التأمين ألف جنيه فتكون مجموع الطالبات المتوقع أن تدفعها شركة التأمين مرة واحدة في نهاية العشرين سنة هو 7698698000 جنيه.
وبما أن المطالبات سوف تدفع في نهاية عشرين سنة، فإن القيمة الحالية للجنيه الواحد بمعدل 2% سنويًا تكون 0.67297. ويكون إجمالي القيمة الحالية للمطالبات المتوقعة هو مبلغ 306 مليمًا و5180999279 جنيهًا.
وبقسمة هذا الرقم الذي يمثل التكلفة الكلية يوم التعاقد على عدد الأشخاص في تمام السن 40 الذين عملت لهم هذه الوثيقة وعددهم 9241359 شخصًا ينتج القسط الوحيد الصافي للوثيقة والذي يبلغ 132 مليمًا و560 جنيهًا.
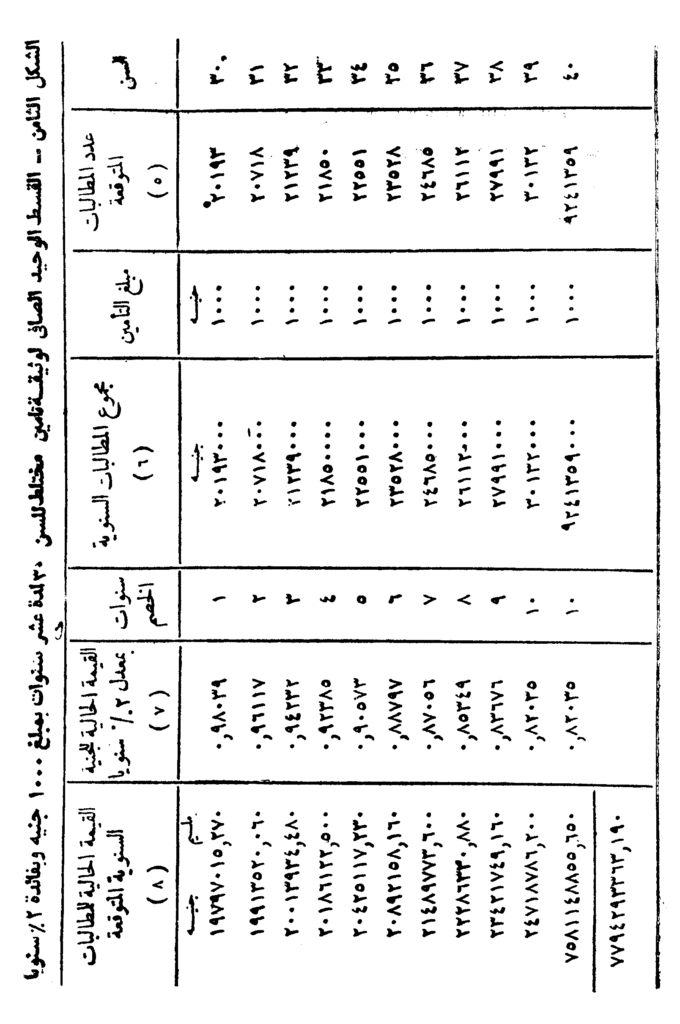
حساب القسط الوحيد الصافي لدفعة حياة مؤقتة عادية
عند حساب القسط الوحيد الصافي لدفعة حياة مؤقتة عادية – أو لأي نوع آخر من الأنواع المختلفة للدفعات – تتبع نفس الخطوات العشر السابق الإشارة إليها مع استعمال جداول الحياة وجداول الفائدة المركبة.
والفرق الوحيد الذي سوف يلاحظ في حساب القسط أن المطالبات تترتب على وجود الأشخاص أحياء آخر كل سنة من سنوات المدة المتفق عليها، بمعنى أن شركة التأمين يكون عليها أن تدفع قيمة الدفعة في نهاية كل سنة من تلك المدة لأولئك الموجودين على قيد الحياة عند استحقاقها.
فإذا أريد حساب القسط الوحيد الصافي لدفعة حياة عادية سنوية قدرها مائة جنيه تصدر للأشخاص في سن الثلاثين ولمدة عشر سنوات، فإنه يمكن تطبيق الخطوات السابقة ووضع البيانات الخاصة بها والناتجة عنها في جدول كما هو مين بالشكل التالي.
ويلاحظ من الجداول أن عدد المطالبات المتوقعة خلال مدة العشر سنوات تكون عبارة عن عدد الأحياء في آخر كل سنة من سنوات الوثيقة، أي عدد الأحياء في تمام السن 31 والسن 32 وهكذا حتى نصل إلى عدد الأحياء في تمام السن 40. حيث أن هؤلاء الأشخاص هم الذين سوف يطالبون شركة التأمين بدفع قيمة دفعة الحياة لكل منهم.
ومجموع العمود الأخير بالجدول يمثل مجموع القيم الحالية للمطالبات المتوقعة والتي تمثل التكلفة الكلية للوثيقة في تاريخ التعاقد، وقد بلغت هذه التكلفة 457 مليمًا و8409093026 جنيه. وبقسمة هذا المبلغ على عدد الأشخاص الأحياء في تمام السن 30 وعددهم 9480358 – وهو السن الذي تم فيه التعاقد على الوثيقة – ينتج القسط الوحيد الصافي لوثيقة دفعة حياة عادية سنوية قدرها مئة جنيه لشخص في تمام السن 30 ولمدة عشر سنوات وقد بلغ 2 مليم و887 جنيهًا.
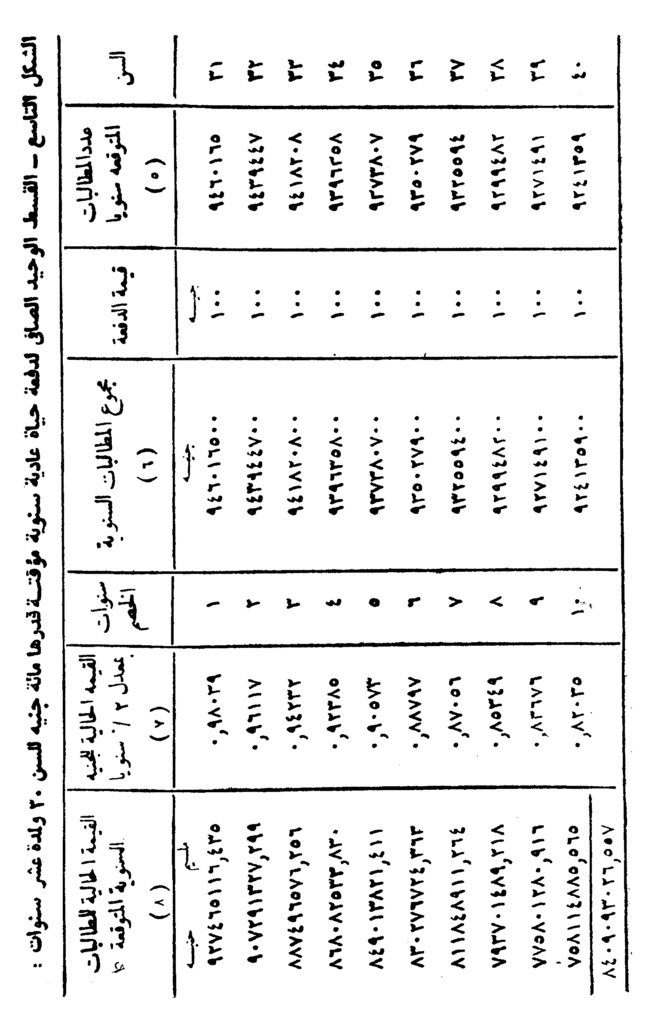
حساب القسط الوحيد الصافي لدفعة حياة مؤقتة فورية
أما إذا كانت دفعة الحياة فورية فإنه يلاحظ أن عدد المطالبات المتوقعة يمثل عدد الأحياء أول كل سنة من سنوات التعاقد. كما أن سنوات الخصم تتغير إذ أن المطالبات الخاصة بالسنة الأولى سوف تدفع فورًا. ومطالبات السنة الثانية تدفع في أول السنة الثانية أي بعد سنة واحدة. وهكذا حتى نجد أن مطالبات السنة الأخيرة تدفع بعد تسع سنوات فقط.
وسوف يؤدي التغير السابق بشقيه إلى تغير بالتبعية في القيمة الحالية للمطالبات السنوية المتوقعة مما يترتب عليه تغيرًا في قيمة القسط الوحيد الصافي للدفعة المؤقتة.
فإذا أريد إعادة حساب القسط الوحيد الصافي للدفعة السابق الإشارة إليها في المثال السابق إذا كانت فورية، فإن الجدول التالي يوضح البيانات الخاصة بها. ومنه يتضح أن المطالبات المتوقعة عن السنة الأولى تدفع للأحياء في تمام السن ثلاثين فورًا، ومطالبات السنة الثانية تدفع للأحياء في تمام السن واحد وثلاثين. وهكذا فإن المطالبات الخاصة بالسنة الأخيرة تدفع للأحياء في تمام السن 39.
مطالبات السنة الأولى
كذلك فإن مطالبات السنة الأولى تدفع فورًا. وعلى ذلك فإن قيمة الجنيه لن تتغير، أما مطالبات السنة الثانية فتدفع بعد سنة وعلى ذلك فإن القيمة الحالية للجنيه تحسب عن سنة. وهكذا إلى أن نجد أن مطالبات السنة الأخيرة تدفع بعد تسع سنوات. وعلى ذلك فإن القيمة الحالية للجنيه تحسب عن تسع سنوات.
ونتيجة لهذا الاختلاف في حساب عدد المطالبات والقيمة الحالية للجنيه فإن القسط الوحيد الصافي في هذا المثال لا بد وأن يكون أكبر في القيمة عن مثيله في المثال السابق. ولذلك فعند قسمة مجموع القيم الحالية للمطالبات السنوية المتوقعة – وهو العمود الأخير في الجدول الموجود في الشكل التالي – على الأحياء في تمام السن 30 وهم الذين يتقاسمون تكلفة الوثيقة وعددهم 9480358 شخصًا، نجد أن القسط يبلغ 907034 وهو يزيد فعلاً عن مثيله في حالة وثيقة الدفعة العادية.
حساب القسط الوحيد الصافي لوثيقة مركبة
عند حساب القسط الوحيد الصافي لوثيقة مركبة تتبع نفس الخطوات العشر السابق ذكرها مع ملاحظة أن عدد المطالبات ربما يتكرر في سنة أو أكثر من سنوات الوثيقة.
كما أن قيمة هذه المطالبات تختلف من نوع إلى آخر في نفس السنة. وفي جميع الحالات يستعمل جدول الحياة كما يستعمل جدول الفوائد المركبة للمعاونة في حساب المطالبات وقيمتها الحالية.
فإذا أريد حساب القسط الوحيد الصافي الذي يدفعه أولئك الذين في تمام السن 30 لكي يحصلوا على المزايا الآتية من شركة التأمين:
- ألف جنيه تدفع للورثة في حالة وفاة المؤمن على حياته خلال الخمس سنوات الأولى.
- ألفين من الجنيهات تدفع للورثة في حالة وفاة المؤمن على حياته خلال الخمس سنوات الثانية.
- ثلاثة آلاف جنيه تدفع للمؤمن على حياته مرة واحدة في حالة بقائه حيًا في نهاية العشر سنوات.
ويمكن تطبيق الخطوات العشر وجمع البيانات والنتائج ووضعها في جدول ليسهل حساب القسط الوحيد الصافي منه وذلك كما هو موضح بالشكل التالي.
شكل توضيحي
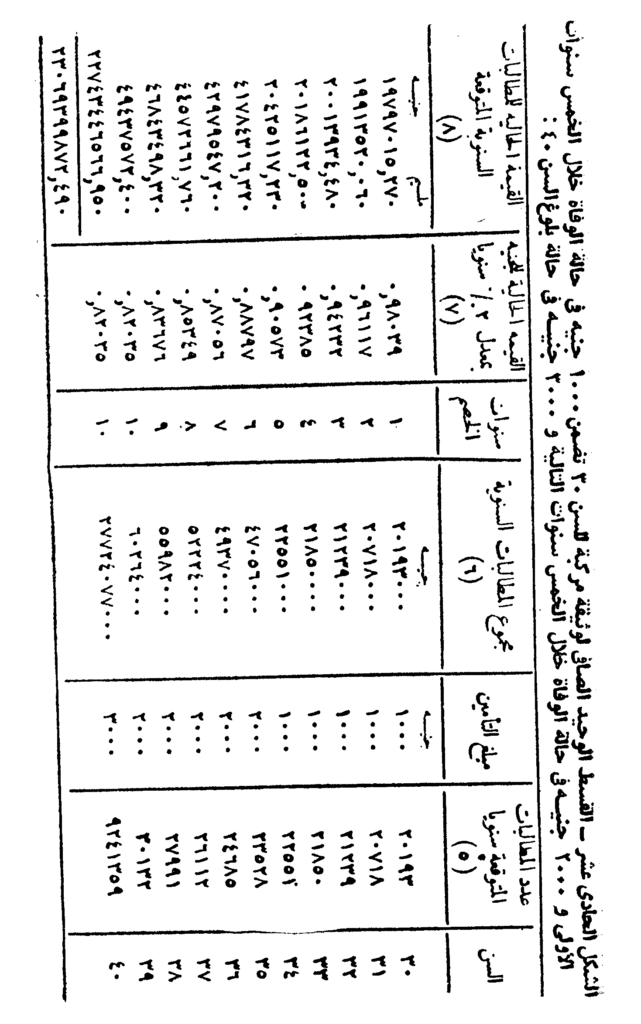
ويلاحظ أن عدد المطالبات المتوقعة الموجودة في الجدول المذكور تقع في قطاعين مختلفين، القطاع الأول هو عدد المطالبات الناتج عن عدد الوفيات خلال السنوات العشر، والقطاع الثاني هو عدد الأحياء في تمام السن 40. كما يلاحظ أن مبلغ التأمين خلال الخمس سنوات الأولى هو 1000 جنيه، وخلال الخمس سنوات الثانية هو 2000 جنيه، أما في تمام السن 40 – أي في نهاية العشر سنوات – فهو 3000 جنيه، وذلك حسب نص الحالة التي يراد حساب القسط الوحيد الصافي عنها. وأخيرًا يلاحظ أن مجموع المطالبات السنوية خلال السنوات الخمس الأولى يحسب على أساس عدد وفيات كل سنة منها وبفرض أن شركة التأمين تتعهد بدفع مبلغ ألف جنيه لكل حالة.
أما مجموع المطالبات السنوية خلال الخمس سنوات الثانية فإنه يحسب على أساس عدد وفيات كل سنة منها ولكن بفرض أن الشركة تتعهد بدفع مبلغ ألفين من الجنيهات لكل حالة. أما مجموع مطالبات السن 40 فإنه يحسب على أساس عدد الأشخاص الذين يبلغون تمام السن 40 وبفرض أن الشركة تتعهد بدفع مبلغ ثلاثة آلاف جنيه لكل منهم.
وأما باقي خطوات عمل الجداول واستنتاج البيانات الخاصة به فلا تختلف عن تلك السابق الكلام عنها في الحالات السابقة. هذا ويلاحظ أن مجموع القيمة الحالية للمطالبات السنوية المتوقعة – وهي التكلفة الكلية يوم عقد الوثيقة – قد بلغت في هذه الحالة بالذات 490 مليمًا و23069399872 جنيهًا. وبقسمة هذا الرقم على عدد الأشخاص الذين في تمام السن 30 وهم 9480358 شخصًا والذين يفترض فيهم المشاركة في تحمل هذه التكلفة لتمتعهم بمزايا هذا التأمين، ينتج القسط الوحيد الصافي لهذه الوثيقة ويبلغ 389 مليمًا و2433 جنيهًا.
حساب القسط السنوي
يصعب على شركات التأمين بيع وثائق تأمينات الحياة بأنواعها المختلفة على أساس القسط الوحيد. إذ أنه قد وجدنا أن ذلك القسط يبلغ رقما مرتفعًا حتى بالنسبة لمبالغ التأمين المتواضعة. هذا مع ملاحظة أنه لابد من إضافة أعباء القسط من مصروفات وأرباح مما يزيد من كبر قيمة القسط وعدم إمكان المستأمن سداده مرة واحدة. في هذا القسم سوف يتم شرح القسط السنوي أو Annual Premium.
القسط الطبيعي السنوي
يمكن علاج هذه المشكلة – مشكلة عدم قدرة المستأمن على دفع القسط الوحيد دفعة واحدة عند التعاقد على تأمين لمدة طويلة – بإحدى طريقتين، الأولى أن يقوم المستأمن بدفع تكلفة التأمين سنة بعد أخرى على أساس السن الفعلي لكل سنة ويدفع القسط في أول كل سنة يريد دفع تكلفتها. ويطلق على القسط في هذه الطريقة القسط الطبيعي أو Natural Premium. ويلاحظ أن القسط الطبيعي هو قسط سنوي يتزايد من سنة لأخرى لتزايد احتمال وفاة الشخص من سنة لأخرى أيضًا. ويعتمد القسط الطبيعي في حسابه على احتمال وفاة الشخص خلال السنة والقيمة الحالية للجنيه لمدة سنة على أساس أن التعويض أو المطالبة تتم في نهاية السنة بالنسبة للمتوفين خلال السنة.
والطريقة السابقة تخلق مشاكل متعددة للمستأمنين ولشركة التأمين. إذ أن القسط الطبيعي السنوي يحتاج إلى حساب قسط كل سنة على حدة ويتزايد من سنة لأخرى مما يشجع المستأمن على الانسحاب من التأمين في الوقت الذي يرى فيه أن القسط أصبح غير محتمل. أضف إلى ذلك أن تغير قيمة القسط من سنة إلى أخرى يجعل من الصعب على المستأمن أن يتذكر قيمته كما يتعذر عليه مراجعة طريقة حسابه.
ففي حالة وثيقة تأمين مؤقت للسن 30 لمدة عشر سنوات وبمبلغ 1000 جنيه والتي سبق أن حسب قسطها الوحيد الصافي حسب البيانات الواردة في الشكل المرفق لتلك الفقرة، فإنه يمكن التوصل إلى حساب القسط السنوي الطبيعي من الشكل التالي والمأخوذة بياناته من الجدول الأمريكي والشكل السابق ذكره:
شكل توضيحي
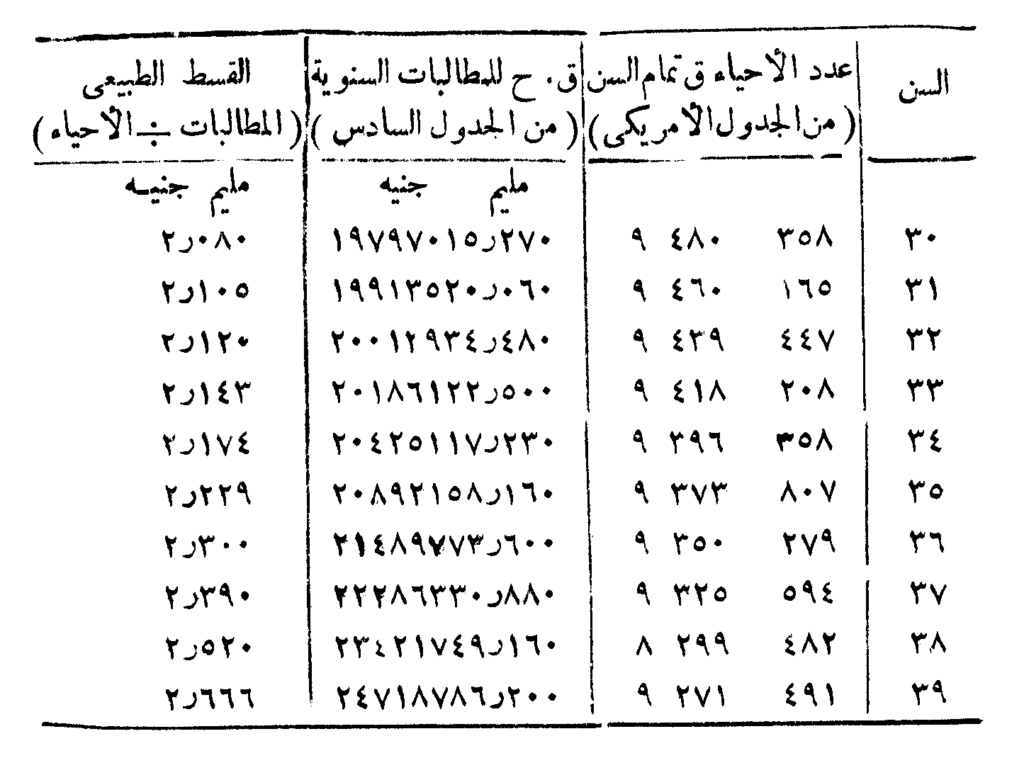
والجدول أعلاه والرسم البياني الذي يوضح البيانات الواردة في الجدول ويبين العلاقة بين العمر وقيمة القسط الطبيعي السنوي الوارد في الشكل التالي يوضحان الصعوبات العملية التي تترتب على التفكير في استعمال القسط الطبيعي السنوي.
القسط السنوي المتساوي
أما الطريقة الثانية فهي أن يقوم المستأمن بدفع قسط سنوي متساوي طول مدة قيامه بسداد القسط. وبذلك يعالج معظم المشاكل السابق الإشارة إليها.
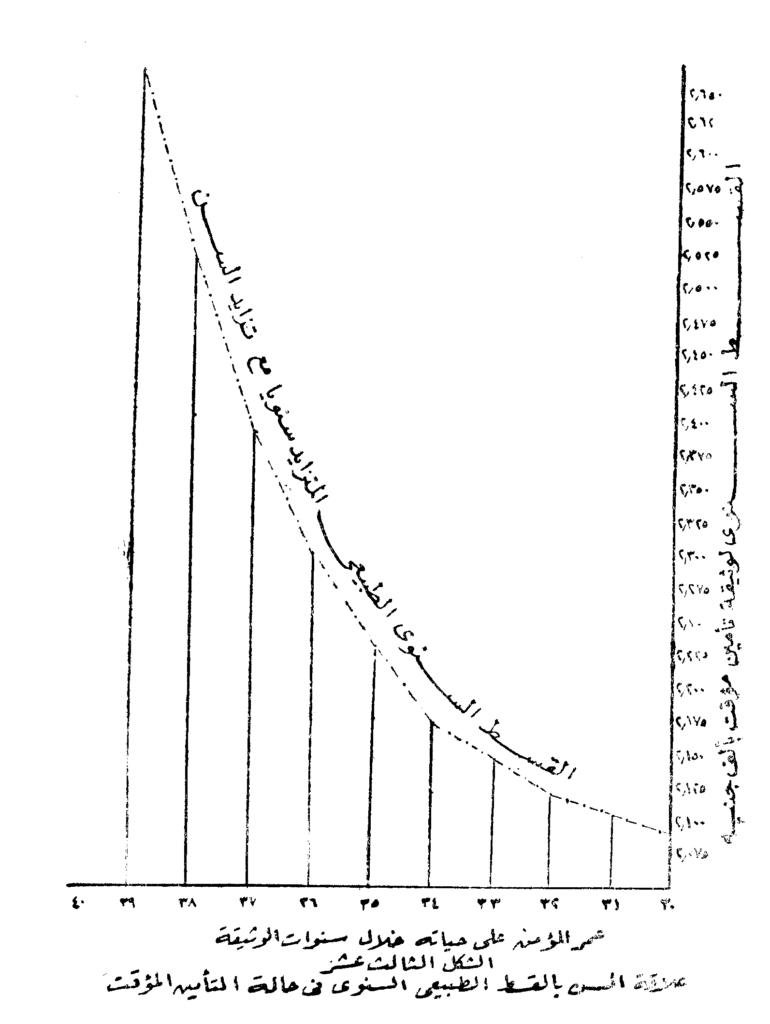
هذا بالإضافة إلى أن القسط السنوي المتساوي الصافي أو Net Annual Premium يكون أكبر من التكلفة الفعلية للتأمين في السنوات الأولى من التعاقد، كما يكون أقل من تلك التكلفة في السنوات الأخيرة، وهذه الظاهرة تحتم على المستأمن الاستمرار في دفع الأقساط سنة بعد أخرى حيث أن الرصيد الزيادة في القسط أو الأقساط التي دفعها في السنوات الأولى تكون عادة عرضة للضياع كليًا أو جزئيًا إذا ما انسحب من التأمين.
وهذه الزيادة في الأقساط المدفوعة خلال السنوات الأولى توضع في احتياطي خاص بها يطلق عليه الاحتياطي الرياضي أو الحسابي أو الفني Mathematical Reserve.
وعادة ما تسمح شروط وثيقة تأمين الحياة بصرف جزء كبير من هذا الاحتياطي إلى المستأمن في حالة توقفه عن دفع الأقساط وانسحابه من التأمين بشرط أن يكون قد سدد أقساط سنتين أو ثلاثة على الأقل. ويقال أن الشخص في هذه الحالة قد قام بتصفية وثيقة التأمين واستلم قيمة التصفية أو Cash Value.
طريقه تحديد القسط السنوي المتساوي
من البديهي أن يستخدم القسط الوحيد الصافي السابق الحصول عليه في الحالات التسع السابقة للحصول على القسط السنوي المتساوي. ومن البديهي أيضًا أن القسط الوحيد الصافي لا بد وأن يساوي القيمة الحالية للقسط السنوي المتساوي الصافي. ومن البديهي أخيرًا أن القيمة الحالية للقسط السنوي المتساوي الصافي ما هي إلا القسط الوحيد الصافي لدفعة حياة قيمة كل منها القسط السنوي المتساوي، حيث أن الأخير يدفع سنويًا في حالة بقاء المؤمن على حياته حيًا فهو إذن يمثل دفعة حياة ولكنها فورية حيث أن القسط السنوي يدفع أول كل سنة.
مما سبق يمكن الوصول إلى المعادلة الآتية:
القسط الوحيد للوثيقة = القيمة الحالية للقسط السنوي (الذي يمثل دفعة حياة)
القسط الوحيد للوثيقة = القسط الوحيد لدفعة حياة سنوية فورية قدر كل منها القسط السنوي
أو أن:
القسط الوحيد للوثيقة= القسط السنوي (قيمة الدفعة) × القسط الوحيد لدفعة حياة قدر كل منها جنيها
إذن:
القسط السنوي = القسط الوحيد ÷ القسط الوحيد الدفعة حياة قدر كل منها جنيها واحدًا ومدتها مدة دفع القسط السنوي
وعلى ذلك تكون الخطوات التي تتبع في حساب القسط السنوي المتساوي الصافي لوثيقة تأمين أيًا كان نوعها هي كالآتي:
- تحديد القسط الوحيد الصافي للوثيقة.
- تحديد القسط الوحيد الصافي لدفعة حياة سنوية فورية قدر كل منها جنيهًا واحدًا تدفع لمدة سداد القسط السنوي.
- ثم تحديد القسط السنوي المتساوي الصافي للوثيقة بقسمة القسط الوحيد الصافي لها على القسط الوحيد الصافي للدفعة.
حساب القسط السنوي المتساوي الصافي لوثيقة مركبة
إذا فرض أن لدينا الوثيقة المركبة التي جاء ذكرها في الحالة الأخيرة عند حساب القسط الوحيد الصافي. وإذا أريد حساب القسط السنوي المتساوي لها والذي يدفع طول مدة العقد (أي القسط السنوي العادي). فإنه يمكن التوصل إلى ذلك كالآتي:
- القسط الوحيد الصافي للوثيقة 2433.389 من الحالة السابقة.
- القسط الوحيد الصافي لدفعة حياة قدرها جنيه واحد للسن 30 ولمدة سداد القسط السنوي وهي عشر سنوات وتحسب من الجدول الموجود بالشكل السابق الإشارة إليه عند حساب القسط الوحيد الصافي الدفعة حياة فورية لسن 30 ولمدة عشر سنوات، إلا أن قيمة الدفعة في ذلك المثال كانت مئة جنيه.
بما أن الدفعة المطلوب إيجاد قسطها الوحيد في حالتنا هذه قيمتها جنيه واحد، فإنه يتحتم علينا قسمة القسط الوحيد الصافي السابق الحصول عليه من الشكل السابق وقدره 907.034 على مئة جنيه لكي نحصل على القسط الوحيد الصافي لدفعة فورية قدرها جنبه واحد، ويبلغ قيمته 9.07 جنيه.
- القسط السنوي المتساوي الصافي ينتج من قسمة القسط الوحيد الصافي للوثيقة على القسط الوحيد الصافي لدفعة حياة قدرها جنيه واحد لمدة دفع القسط.
أي أن:
القسط السنوي = 2443.389 ÷ 9.070 = 368.279 جنيه.
استخدام التوقع الرياضي في حساب الأقساط
ذكرنا في الفصل الثاني (موضوع قياس الخطر) أن التوقع الرياضي يعتبر أحد المقاييس التي تستخدم في قياس الخطر ومشتقاته. كما ذكرنا أيضًا أن التوقع الرياضي هو قسط التأمين أو قسط الرهان ويحسب في حالتين بالنسبة للتاريخ الذي يدفع فيه قيمة مبلغ التأمين أو مبلغ الرهان. فإذا اتفق على دفع المبلغ فورًا – وهذا لن يتأتى إلا إذا كان الحادث موضوع الرهان أو التأمين متوقع حدوثه في نفس الوقت الذي يتم فيه الاتفاق على دفعه – كان التوقع المستعمل هو التوقع الرياضي العاجل – وهو الذي لا يدخل في تكوينه عامل الفائدة – وهذا النوع من التوقع الرياضي يستعمل فعلاً في حالات الرهان العاجل كما يستعمل في حساب أقساط وثائق التأمينات العامة التي تعقد لمدة أقصاها سنة ويتوقع المؤمن أن يدفع مبلغ الخسارة أو التعويض خلال السنة وربما بعد أيام أو أسابيع من التعاقد مما يتطلب الاحتفاظ بالأقساط المحصلة في صورة أموال سائلة أو شبه سائلة فيصعب استثمارها استثمارًا مجزيًا.
أما في حالة وثائق تأمينات الحياة فقد لاحظنا عند حساب الأقساط السنوية أو الوحيدة أنها تبقى لدى شركات التأمين لمدة طويلة. مما ييسر لها الأمر لاستثمارها خلال مدة التعاقد فيعود عليها ذلك بعائد استثمار مجزِ. ويترتب على هذه الظاهرة أن تقوم شركات التأمين بحساب أقساط تأمين وثائق الحياة على أساس أن تلك الأقساط سوف تستثمر عند تحصيلها. وعلى ذلك فهي تكون مستعدة لدفع جزء من عائد الاستثمار لدافعي الأقساط أنفسهم.
ولذلك يستخدم معدل فائدة منخفض عادة عند حساب القسط. ويترتب على كل هذا أن التوقع الرياضي الذي يستعمل في حساب أقساط وثائق الحياة هو التوقع الرياضي الآجل والذي يدخل في حسابه عامل الفائدة المركبة وينص على أن:
التوقع الرياضي الآجل = مبلغ التأمين × الاحتمال × القيمة الحالية للجنيه
مثال تطبيقي
فإذا كان المطلوب حساب القسط الوحيد الصافي لوقفية بحتة بمبلغ ألف جنيه تصدر لشخص في سن الأربعين ولمدة عشرين سنة مثلاً، وكان معدل الفائدة المركبة المستعمل في حساب القسط هو 2% سنويًا، فإنه يمكن الوصول إلى قيمة القسط بمعادلة التوقع الرياضي الأجل كالآتي:
القسط الوحيد = مبلغ التأمين × احتمال أن شخصًا في تمام السن 40 يبقى حيًا إلى تمام السن 60 × القيمة الحالية للجنيه عشرين سنة بمعدل 2%
= 1000 × ((عدد الأحياء في تمام السن 60) ÷ (عدد الأحياء في تمام السن .4)) × ح 30 بمعدل 2%
= 1000 × (7698698 ÷ 9241359) × 0.67297
وهذا يساوي = 560.632 جنيه.
أما إذا كان المطلوب حساب القسط الوحيد الصافي لوثيقة تأمين مؤقت بمبلغ ألف جنيه لمدة عشر سنوات لشخص في تمام السن 30، وكان معدل الفائدة المركبة المستعمل هو 2% سنويًا، فإنه يمكن الوصول إلى قيمة القسط الوحيد الصافي بمعادلة التوقع الرياضي الآجل كالآتي:
القسط الوحيد = مبلغ التأمين × احتمال أن الشخص في تمام السن 30 يموت خلال مدة عشر سنوات × القيمة الحالية للجنيه عن كل سنه من سنوات الدفع
= مبلغ التأمين × ((احتمال الوفاة خلال السنة الأولى × ح) + (احتمال الوفاة خلال السنة الثانية × ح 2) + … + (احتمال الوفاة خلال السنة العاشرة × ح 10) بمعدل 2%)
= 1000 × ((20193 ÷ 9480358 × 0.98039) + (20718 ÷ 9480358 × 0.96117) + ….. + (30132 ÷ 9480358 × 0.82035)
أي أنه يساوي = 22.483 جنيه.
جدول الرموز الحسابية
لاحظنا عند حساب الأقساط الوحيدة والسنوية الصافية لجميع أنواع وثائق تأمينات الحياة سواء بطريقة المطالبات المتوقعة المجمعة أو بطريقة التوقع الرياضي الآجل أننا نضطر إلى اللجوء إلى عمليات حسابية موسعة تعتمد على أرقام مستخرجة من جدول الحياة وأرقام أخرى مستخرجة من جدول الفائدة المركبة. وتنحصر الأرقام المستخرجة من جدول الحياة في نوعين هما:
- عدد الأحياء في السن (س) وترمز له بالرمز ح س (يلاحظ أنها مكتوبة بخط النسخ حتى يمكن التفرقة بينها وبين القيمة الحالية للجنيه والتي تكتب دائمًا بخط الرقعة ح).
- وعدد الوفيات خلال سنة أي بين السن (س) والسن (س + 1) ولنرمز له بالرمز و س.
كما تنحصر الأرقام المستخرجة من جدول الفائدة المركبة والمستخدمة في حساب القسط في القيمة الحالية للجنيه عن مدة (س) وترمز لها بالرمز حـ س.
كما لاحظنا أننا نضطر دائمًا إلى إجراء عمليات ضرب بين عدد الأحياء أو عدد الوفيات من ناحية وبين القيمة الحالية للجنيه من ناحية أخرى. أي أننا عادة ما نقوم بضرب ح س × حـ س أو ضرب و س × حـ س ، وهذا يستدعي بذل مجهود ووقت کبيرين.
لذلك قام الرياضيون بتجهيز جداول تعطى ناتج الضرب هذا بعد تعديل وتحور في المدة التي بحسب عنها القيمة الحالية للجنيه. وتساعد تلك الجدول – التي يطلق عليها جداول الرموز الحسابية – على حساب أقساط وثائق تأمينات الحياة بطريقة حسابية أسهل من الطرق المطولة السابقة.
ومن أمثلة الرموز الحسابية الخاصة بحساب الأقساط ما يلي:
الرمز د س
ويمثل حاصل ضرب عدد الأحياء في تمام السن (س) في القيمة الحالية للجنيه عن مدة قدرها (س) أي قدرها السن الخاص بالشخص الذي يراد حساب قسط وثيقته.
أي أن:
د س = ح س x حـ س
وهذا الرمز الحسابي يفيد في حساب مطالبات الحياة في سن معين مثل حالة الوقفية البحتة. أما إذا كانت مطالبات الحياة متكررة مثل دفعات المعاش فإنه يتحتم علينا جمع د س + د س + … + 1 + … وهكذا حتى نهاية مدة سداد الدفعة
الرمز ن س
ويمثل مجموع مفردات الرمز الحسابي الأول وهو د س حتى نهاية الجدول.
أي أن:
ن س = د س + د س + … + 1 + … إلى نهاية الجدول، وبذلك يمكن استخدام رقم واحد مأخوذ من جدول الرموز الحسابية بدلاً من جمع عدة أرقام متتالية كبيرة الحجم. ويفيد هذا الرمز في حساب أقساط وثائق دفعات الحياة.
الرمز ج س
ويمثل حاصل ضرب عدد الوفيات خلال سنة بعد تمام السن (س) في القيمة الحالية للجنيه عن مدة قدرها (س + ۱) على أساس أن مبلغ تأمين الوفاة يدفع في نهاية سنة الوفاة أي بعد مضي سنة كاملة من سنوات العقد.
أي أن:
ج س = و س × حـ س + 1
وهذا الرمز يفيد في حساب مطالبات الوفاة السنوية. أي أنه يحسب القيمة الحالية للمطالبات السنوية كل سنة على حدة.
الرمز م س
ويمثل مجموع مفردات الرمز الحسابي ج س حتى نهاية الجدول.
أي أن:
م س = ج س + ج س + 1 + … إلى نهاية الجدول.
وبذلك يمكن استخدام رقم واحد مأخوذ من جدول الرموز الحسابية بدلاً من جمع أرقام القيمة الحالية للتعويضات سنة بعد أخرى. ويفيد هذا الرمز في حساب أقساط وثائق تأمينات الوفاة بأشكالها المختلفة مثل التأمين المؤقت والمؤجل المؤقت ومدى الحياة ومدى الحياة المؤجل.
حالة التوقف عن سداد الأقساط الدورية
كثيرًا ما يحدث أن يتوقف المستأمن عن سداد أقساط التأمين الدورية. والإجراءات التي تتبعها عادة شركات التأمين في هذه الحالة يمكن تلخيصها فيما يلي:
أولاً: إذا كان عدد الأقساط السنوية المسددة بالكامل أقل من عدد معين – ثلاثة مثلاً – فإن الشركة تلغي العقد وتستولي على جميع المبالغ التي تكون قد تسلمتها. فمثلاً بالنسبة لوثيقة قسطها السنوي 50 جنيهًا دفع عنها المؤمن قسط سنة واحدة ثم توقف عن السداد فإن الشركة لا ترد شيئًا إلى العميل ويصبح هذا القسط حقًا مكتسبًا للشركة. ويرجع ذلك إلى أن الشركة دفعت عمولات للمنتج إلى جانب جميع المصاريف الإدارية المنفقة. هذا بخلاف تغطية خطر الوفاة بالكامل خلال السنة. فإذا ما حدثت الوفاة خلال هذه السنة تستحق دفع مبلغ التأمين بالكامل.
ثانيًا: إذا كان المستأمن قد سدد أقساط سنوية عن ثلاثة سنوات كاملة فإن للمستأمن الحق في أن يختار حلاً من عدة حلول والتي منها ما يلي:
- التنازل عن العقد كلية في مقابل الحصول على قيمة التصفية والتي تحسب عادة على أساس نسبة من مبلغ التأمين بنسبة عدد الأقساط المسددة إلى عدد الأقساط التي كان على المستأمن أن يسددها.
- تحويل العقد إلى عقد مخفض، أي عقد بنفس شروط العقد الأصلي ولكن مع تخفيض مبلغ التأمين بما يقابل الأقساط السنوية التي كان محتملاً تحصيلها في المستقبل بنفس طريقة التخفيض السابقة مع إضافة فائدة بمعدل مرتفع نسبيًا ۔ عادة 5% سنويًا – على قيمة التصفية.
- إقراض القسط بضمان الوثيقة مع تحميل القسط بفوائد تأخير ترتفع عادة لتصل إلى 6.5% سنويًا.
وعلى المستأمن أن يختار أحد هذه الحلول خلال مدة معينة من تاريخ توقفه عن السداد. وإلا كان لشركة التأمين الحق في اتخاذ القرار الأفيد لها ماليًا.
إعادة سريان وثيقة تأمين على الحياة
إذا توقف المستأمن عن سداد الأقساط وترتب على ذلك إلغاء العقد بسبب عدم دفع الحد الأدنى للأقساط السنوية أو تحويله إلى عقد مخفض، فإنه مع ذلك يكون له الحق في إعادة سريان مفعول عقده بناء على طلبه وذلك بالشروط الآتية:
- أن يدفع جميع الأقساط المتأخرة وفوائدها.
- أن يكون المؤمن عليه في صحة سليمة، أي صالحًا للتأمين عليه.
والشرط الأخير شرط هام، إذ بدونه نجد أن العملاء الذين يلغون عقودهم أو يحولونها إلى عقود مخفضة ثم يجدون أن حالتهم الصحية قد ساءت يعودون للتأمين وبذا يعرضون الشركة لظاهرة الأخطار الرديئة.
وعلى هذا نجد أن الشركة تشترط توقيع الكشف الطبي على المستأمن الذي يطلب إعادة السريان، وتكون مصروفات هذا الكشف على حساب العميل.
فإن اتضح أن العميل لائق من الناحية الصحية أقرت الشركة إعادة سريان مفعول الوثيقة وإلا فإن الشركة ترفض إعادة السريان أو تقبله بشروط معدلة.
هذا ويلاحظ أنه إذا طلب العميل إعادة السريان خلال مدة وجيزة من تاريخ التوقف عن السداد لا تزيد عن سنة فإن الشركة قد تلغي إجراءات الكشف الطبي.
المصدر
- كتاب الخطر والتأمين – الأصول العلمية والعملية. تأليف: الدكتور سلامة عبد الله، كلية التجارة، جامعة القاهرة، 1967، 1974.
- موسوعة التأمين، العلوم المالية والمصرفية، مركز البحوث والدراسات متعدد التخصصات، 2023.