مخطط الجسم الحر

رسم مخطط الجسم الحر

تتضمن الخطوة الأولى في وصف وتحليل معظم الظواهر في الفيزياء الرسم الدقيق لمخطط الجسم الحر. تم استخدام مخططات الجسم الحر في أمثلة من خلال هذا الفصل. تذكّر أن مخطط الجسم الحر يجب أن يتضمن فقط القوى الخارجية التي تعمل على الجسم محل الاهتمام. بمجرد رسم مخطط دقيق للجسم الحر، يمكننا تطبيق قانون نيوتن الأول إذا كان الجسم في حالة توازن (قوى متوازنة؛ أي في حالة أن تكون محصلة القوى تساوي صفر، F_net = 0) أو بتطبيق قانون نيوتن الثاني إذا كان الجسم يتسارع (قوى غير متوازنة؛ أي أن محصلة القوى F_net لا تساوي صفر).

في موضوع القوى، قدمنا ​​استراتيجية مختصرة لحل المسائل لمساعدتك على فهم مخططات الجسم الحر. نضيف هنا بعض التفاصيل إلى الإستراتيجية التي ستساعدك في إنشاء هذه المخططات.

أهداف التعلم:

بنهاية هذا القسم، ستكون قادرًا على:

• شرح قواعد رسم مخطط الجسم الحر
• إنشاء مخططات الجسم الحر لمواقف مختلفة

استراتيجية حل المسائل

التزم بالقواعد التالية عند إنشاء مخطط الجسم الحر وحل مسائل الميكانيكا:

1. ارسم الكائن قيد الدراسة؛ لا يجب أن تكون رسمة فنية. في البداية، قد ترغب في رسم دائرة حول الشيء الذي تريده للتأكد من أنك تركز على تسمية القوى المؤثرة على الكائن. إذا كنت تتعامل مع الكائن على أنه جسيم (بدون حجم أو شكل ولا دوران)، فقم بتمثيل الكائن كنقطة. غالبًا ما نضع هذه النقطة في أصل نظام الإحداثيات xy.
2. قم بتضمين جميع القوى التي تعمل أو تؤثر على الكائن، وتمثل هذه القوى كمتجهات. ضع في اعتبارك أنواع القوى الموصوفة في القوى الشائعة – القوة الطبيعية، والاحتكاك، والتوتر، وقوة الزنبرك – بالإضافة إلى الوزن والقوة المطبقة. لا تقم بتضمين صافي القوى المؤثرة على الجسم. باستثناء الجاذبية، تتطلب جميع القوى التي ناقشناها اتصالًا مباشرًا بالجسم. ومع ذلك، يجب عدم تضمين القوى التي يمارسها الكائن على بيئته. نحن لا نقوم بتضمين كلتا القوتين من الزوج “الفعل ورد الفعل”.
3. قم بتحويل مخطط الجسم الحر إلى مخطط أكثر تفصيلاً يوضح مكونات x و y لقوة معينة (غالبًا ما يكون هذا مفيدًا عند حل مسألة باستخدام قانون نيوتن الأول أو الثاني). في هذه الحالة، ضع خطًا متعرجًا عبر المتجه الأصلي لإظهار أنه لم يعد قيد الاستخدام – فقد تم استبداله بمكوني x و y.
4. إذا كان هناك جسمان أو أكثر في المسألة، فقم برسم مخطط جسم حر منفصل لكل كائن.

ملاحظة: إذا كان هناك تسارع، فإننا لا نقوم بتضمينه مباشرة في مخطط الجسم الحر؛ ومع ذلك، قد يساعد في الإشارة إلى التسارع خارج مخطط الجسم الحر. يمكنك تسميته بلون مختلف للإشارة إلى أنه منفصل عن مخطط الجسم الحر.

تطبيق استراتيجية حل المسائل

دعنا نطبق استراتيجية حل المسائل هذه في رسم مخطط الجسم الحر لمزلقة. في الشكل 5.31 (أ)، يتم سحب مزلقة بالقوة P بزاوية 30 درجة. في الجزء (ب)، نعرض مخططًا للجسم الحر لهذا الموقف، كما هو موضح في الخطوتين 1 و2 من استراتيجية حل المسائل. وفي الجزء (ج)، نعرض جميع القوى من حيث مكوناتها x و y، تمشيًا مع الخطوة 3.

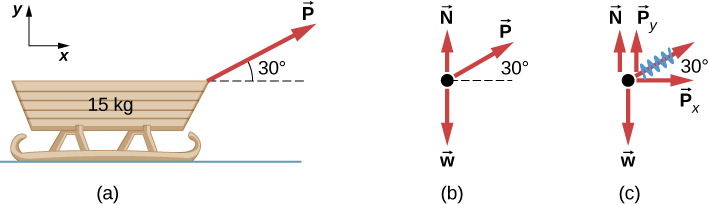
يوضح الشكل (أ) زلاجة وزنها 15 كجم. السهم المسمى P يشير لليمين ولأعلى يشكل زاوية 30 درجة مع الأفقي. الشكل (ب) هو مخطط جسم حر حيث تشير P وN إلى الأعلى وw تشير إلى الأسفل. الشكل (ج) عبارة عن مخطط جسم حر مع P وN وw ومكوّنين من P وهما P_x يشير إلى اليمين وP_y يشير إلى أعلى.

أمثلة على رسم مخطط الجسم الحر

مثال 5.14: مخطط الجسم الحر لكتلتان على مستوى مائل

أنشئ مخطط الجسم الحر للكائن A والكائن B في الشكل 5.32.

إستراتيجية الحل

نتبع الخطوات الأربع المدرجة في استراتيجية حل المسائل.

الحل

نبدأ بإنشاء رسم تخطيطي لأول كائن موضع اهتمام. في الشكل 5.32 (أ) ، يتم عزل الكائن أو الجسم A (محاط بدائرة) ويتم تمثيله بنقطة.

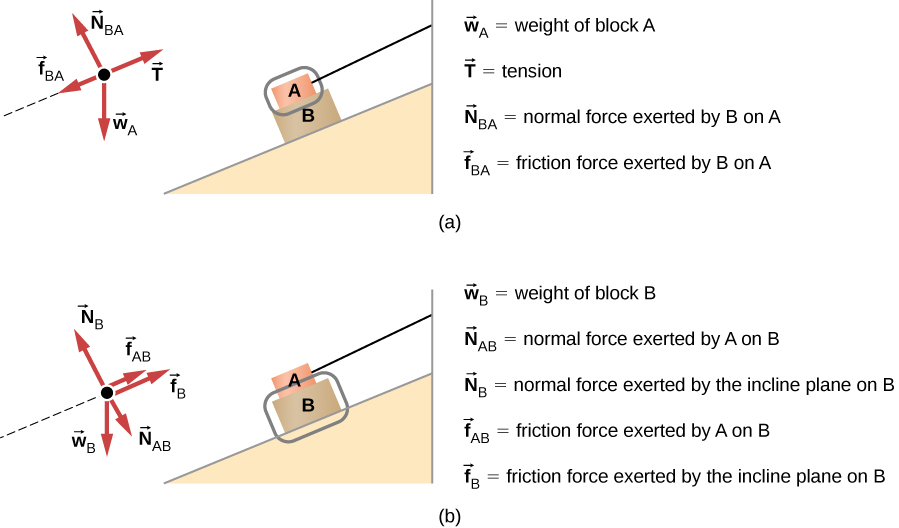
بمقارنة الرسمين، نرى أن الاحتكاك يعمل في الاتجاه المعاكس في الشكلين. لأن الجسم A يواجه قوة تميل إلى سحبه إلى اليمين، يجب أن يعمل الاحتكاك في اتجاه اليسار. نظرًا لأن الكائن B يواجه مكونًا من وزنه يسحبه إلى اليسار، أسفل المنحدر، يجب أن تعارضه قوة الاحتكاك وتعمل على المنحدر. يعمل الاحتكاك دائمًا عكس الاتجاه المقصود للحركة.

نقوم الآن بتضمين أي قوة تؤثر على الجسم. هنا، لا توجد قوة مطبقة أو مؤثرة. يعمل وزن الجسم كقوة تتجه عموديًا لأسفل، ويشير وجود السلك إلى قوة توتر متجهة بعيدًا عن الجسم. يحتوي الكائن A على واجهة واحدة وبالتالي يواجه قوة طبيعية، يتم توجيهها بعيدًا عن الواجهة. مصدر هذه القوة هو الجسم B، وهذه القوة الطبيعية تسمى وفقًا لذلك. نظرًا لأن الكائن B يميل إلى الانزلاق لأسفل، فإن الكائن A يميل إلى الانزلاق لأعلى فيما يتعلق بالواجهة، لذلك يتم توجيه الاحتكاك f_BA لأسفل بالتوازي مع المستوى المائل.

كما هو مذكور في الخطوة 4 من استراتيجية حل المسائل، نقوم بعد ذلك ببناء مخطط الجسم الحر في الشكل 5.32 (ب) باستخدام نفس النهج. يواجه الكائن B قوتان طبيعيتان وقوتي احتكاك نتيجة لوجود سطحين للتلامس. يمارس السطح مع المستوى المائل قوى خارجية من N_B و f_B، والسطح مع الكائن B يمارس القوة الطبيعية N_AB والاحتكاك f_AB؛ يتم توجيه N_AB بعيدًا عن الكائن B، وتعارض f_AB اتجاه الحركة النسبية للكائن B بالنسبة للكائن A.

الدلالة

تم وضع الكائن قيد النظر أو محل الاهتمام في كل جزء من هذه المسألة بدائرة باللون الرمادي. عندما تتعلم كيفية رسم مخططات الجسم الحر لأول مرة، ستجد أنه من المفيد وضع دائرة حول الكائن قبل تحديد القوى التي تعمل على هذا الكائن المحدد. هذا يركز انتباهك، ويمنعك من التفكير في القوى التي لا تؤثر على الجسم.

مثال 5.15: مخطط الجسم الحر لأجسام متلاصقة

يتم تطبيق قوة على كتلتين على اتصال مع بعضهما (متلاصقتين)، كما هو موضح في الشكل التالي.

إستراتيجية الحل

نرسم مخططًا للجسم الحر لكل كتلة. تأكد من مراعاة قانون نيوتن الثالث في منطقة السطح حيث تتلامس الكتلتان.

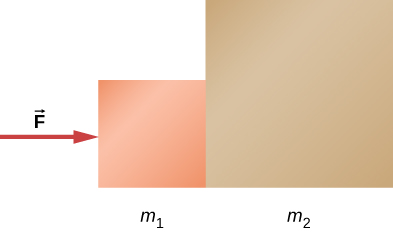
يظهر مربعان على اتصال مع بعضهما البعض. المربع الأصغر على اليسار ويُشار إليه m₁. والمربع الأكبر على اليمين ويشار إليه m₂. السهم الذي يشير إلى اليمين نحو m₁ يمثل القوة F.

الحل

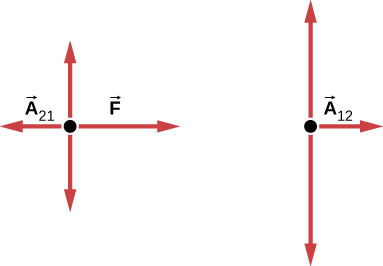
يوضح الشكل مخططين حرين للجسمين. الأول يظهر السهم A₂₁ يشير إلى اليسار والسهم F يشير إلى اليمين. المخطط الثاني يظهر السهم A₁₂ مشيرًا إلى اليمين. يحتوي كلا المخططين أيضًا على أسهم تشير لأعلى ولأسفل.

الدلالة

A⃗₂₁ هي قوة عمل الكتلة m₂ على الكتلة m₁. A⃗₁₂ هي قوة رد فعل الكتلة m₁ على الكتلة m₂. نستخدم مخططات الجسم الحر هذه في تطبيقات قوانين نيوتن.

مثال 5.16: الكتلة على المنضدة (مخططات الكتل المزدوجة)

كتلة تقع على المنضدة، كما هو موضح في الشكل. يتم توصيل حبل خفيف بها ويمر فوق بكرة. الطرف الآخر من الحبل متصل بكتلة ثانية. ويقال أن الكتلتين متقاربتان. الكتلة m₂ تمارس قوة بسبب وزنها، مما يؤدي إلى تسريع النظام (الكتلتان والخيط).

إستراتيجية الحل

نفترض أن الوتر أو الخيط ليس له كتلة، لذا لا يتعين علينا اعتباره كائنًا منفصلاً. نرسم مخططًا للجسم الحر لكل كتلة.

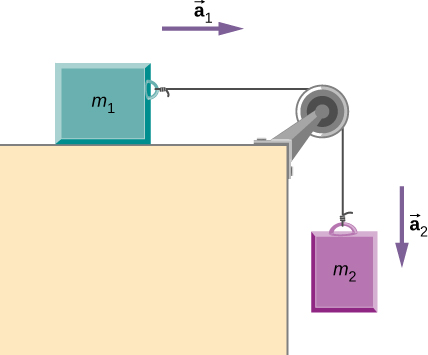
يوضح الشكل الكتلة m₁ الموضوعة على المنضدة. خيط متصل بها يمتد فوق بكرة وأسفل الجانب الأيمن من المنضدة. الكتلة m₂ معلقة منه. يشير السهم a₁ إلى اليمين والسهم a₂ يشير إلى الأسفل.

الحل

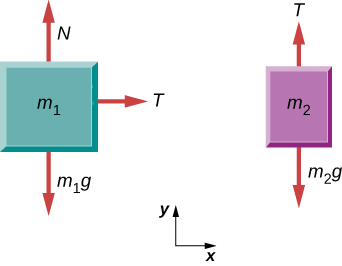
يوضح الشكل (a) الكتلة m₁. والسهم مكتوب عليه N يشير إلى الأعلى منها، والسهم m_1g يشير إلى الأسفل والسهم T يشير إلى اليمين. يوضح الشكل (ب) الكتلة m₂. يشير السهم T لأعلى منها والسهم m_2g يشير إلى الأسفل.

الدلالة

تتسارع كل كتلة (لاحظ التسميات المختلفة الموضحة لـكل من a⃗₁ و a⃗₂)؛ ومع ذلك، بافتراض أن الوتر لا يزال مشدودًا، فإن مقادير التسارع متساوية. وبالتالي، لدينا | a⃗ ₁ | = | a⃗ ₂ |. إذا واصلنا حل المسألة، فيمكننا ببساطة معرفة قيمة العجلة a⃗. نستخدم أيضًا مخططين للجسم الحر لأننا عادةً ما نجد التوتر T، والذي قد يتطلب منا استخدام نظام من معادلتين في هذا النوع من المسائل. التوتر أو الشد هو نفسه في كل من m₁ وm₂.

تحقق من فهمك 5.10

(أ) ارسم مخطط الجسم الحر للوضع الموضح في الشكل التالي. (ب) قم بإعادة رسم المخطط مع إظهار المكونات؛ استخدم محاور x الموازية للمنحدرين.

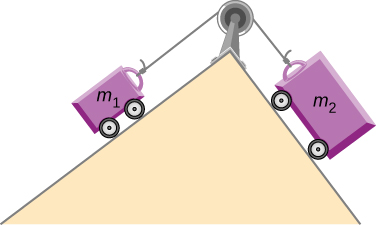
في الشكل أعلاه، عربتان مربوطتان بحبل يمر فوق بكرة على قمة تل. تقع كل عربة على أحد المنحدرات من التل على جانبي البكرة. العربة الموجودة على اليسار m₁ والعربة الموجودة على اليمين m₂.

تعليم تفاعلي

شاهد هذه المحاكاة للتنبؤ نوعيًا بكيفية تأثير قوة خارجية على سرعة واتجاه حركة الجسم. اشرح التأثيرات بمساعدة مخطط الجسم الحر. استخدم مخططات الجسم الحر لرسم مخططات للموضع، والسرعة، والتسارع أو العجلة، والقوة، والعكس بالعكس. اشرح كيف ترتبط المخططات ببعضها البعض. بالنظر إلى سيناريو معين أو مخطط منهم، ارسم المخططات الأربعة.

المراجع

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.