قوانين نيوتن للحركة

قوانين نيوتن للحركة

عندما تقود سيارتك عبر جسر، تتوقع أن تظل مستقرًا. تتوقع أيضًا تسريع سيارتك أو إبطائها استجابة لتغيرات حركة المرور. في كلتا الحالتين، أنت تتعامل مع القوى. القوى الموجودة على الجسر في حالة اتزان، لذلك يبقى الجسر في مكانه. على النقيض من ذلك، فإن القوة التي ينتجها محرك سيارتك تسبب تغييرًا في الحركة. اكتشف إسحاق نيوتن قوانين الحركة التي تصف هذه المواقف والتي سُميت ياسم قوانين نيوتن للحركة.

تؤثر القوى على كل لحظة في حياتك. يتم تثبيت جسمك على الأرض بالقوة ويتم تماسكه بواسطة قوى الجسيمات المشحونة. عندما تفتح بابًا، أو تمشي في الشارع، أو ترفع الشوكة، أو تلمس وجه طفل، فأنت تستخدم القوة. عند التكبير بشكل أعمق، تتماسك ذرات جسمك معًا بواسطة قوى كهربائية، ويتم تجميع قلب الذرة، الذي يسمى النواة، معًا بواسطة أقوى قوة نعرفها – القوة النووية القوية.

الشكل 5.1 جسر البوابة الذهبية، أحد أعظم أعمال الهندسة الحديثة، كان أطول جسر معلق في العالم في عام افتتاحه عام 1937. ولا يزال من بين أطول 10 جسور معلقة حتى كتابة هذه السطور. عند تصميم الجسر وبنائه، ما هي الفيزياء التي يجب أن نأخذها في الاعتبار؟ ما هي القوى التي تؤثر على الجسر؟ ما هي القوى التي تمنع الجسر من السقوط؟ كيف تتفاعل الأبراج والكابلات والأرض للحفاظ على الاستقرار؟ كل هذه الأسئلة وغيرها سوف نجيب عليها في هذا الفصل، قوانين نيوتن للحركة.

مخطط الفصل الخامس

• 5.1 القوى (في هذه الصفحة)
• 5.2 قانون نيوتن الأول
• 5.3 قانون نيوتن الثاني
• 5.4 الكتلة والوزن
• 5.5 قانون نيوتن الثالث
• 5.6 القوى الشائعة
• 5.7 رسم مخططات الجسم الحر

القوى Forces

أهداف القسم

بنهاية هذا القسم، ستكون قادرًا على:

• التمييز بين علم الحركة (الكينماتيكا) والديناميكا
• فهم تعريف القوة وتحديد مخططات بسيطة للجسم الحر
• فهم إستراتيجية حل مسائل قواني نيوتن للحركة
• تحديد وتعريف وحدة قياس القوة، النيوتن
• وصف القوة كمتجه وتحليله

التمييز بين علم الحركة (الكينماتيكا) والديناميكا

تسمى دراسة الحركة علم الحركة (كينماتيكا)، لكن علم الحركة يصف فقط الطريقة التي تتحرك بها الأشياء – سرعتها وتسارعها. الديناميكيات هي دراسة كيفية تأثير القوى على حركة الأجسام والأنظمة. إنه يأخذ في الاعتبار أسباب حركة الأشياء والأنظمة، حيث يتم تحليل أي نظام. أسس الديناميات هي قوانين الحركة التي ذكرها إسحاق نيوتن (1642-1727). تقدم هذه القوانين مثالاً على اتساع وبساطة المبادئ التي تعمل الطبيعة بموجبها. إنها أيضًا قوانين عالمية من حيث أنها تنطبق على المواقف على الأرض وفي الفضاء.

كانت قوانين نيوتن للحركة مجرد جزء واحد من العمل الضخم الذي جعله أسطوريًا (الشكل 5.2). يمثل تطور قوانين نيوتن الانتقال من عصر النهضة إلى العصر الحديث. لم يُكتشف حتى ظهور الفيزياء الحديثة أن قوانين نيوتن تنتج وصفًا جيدًا للحركة فقط عندما تتحرك الأجسام بسرعات أقل بكثير من سرعة الضوء وعندما تكون هذه الأجسام أكبر من حجم معظم الجزيئات (طول القطر حوالي 10^-9 متر). تحدد هذه القيود عالم ميكانيكا نيوتن. في بداية القرن العشرين، طور ألبرت أينشتاين (1879-1955) نظرية النسبية وميكانيكا الكم جنبًا إلى جنب مع العديد من العلماء الآخرين.

ميكانيكا الكم ليس لديها القيود الموجودة في الفيزياء النيوتونية (نسبة إلى نيوتن). كل المواقف التي نأخذها في الاعتبار في هذا الفصل، وجميع المواقف التي تسبق الفصل الخاص بالنظرية النسبية في هذا الكتاب، هي في عالم الفيزياء النيوتونية.

الشكل 5.2 نشر إسحاق نيوتن (1642-1727) عمله الرائع، Philosophiae Naturalis Principia Mathematica في عام 1687. اقترح قوانين علمية لا تزال سارية حتى اليوم لوصف حركة الأشياء (قوانين الحركة). اكتشف نيوتن أيضًا قانون الجاذبية، واخترع حساب التفاضل والتكامل، وقدم مساهمات كبيرة في نظريات الضوء واللون.

تعريف القوة

الديناميكا هي دراسة القوى التي تسبب تحرك الأشياء والأنظمة. لفهم هذا، نحتاج إلى تعريف عملي للقوة. يُعد التعريف الحدسي للقوة – أي الدفع أو السحب – مكانًا جيدًا للبدء. نحن نعلم أن الدفع أو الشد لهما مقدار واتجاه (وبالتالي، فهو كمية متجهة)، لذلك يمكننا تعريف القوة على أنها الدفع أو الشد على جسم بحجم واتجاه محددين. يمكن تمثيل القوة بالمتجهات أو التعبير عنها كمضاعفات للقوة القياسية.

يمكن أن يختلف الدفع أو السحب على جسم ما بشكل كبير في أي من الحجم أو الاتجاه. على سبيل المثال، يمارس المدفع قوة شديدة على قذيفة مدفعية تُطلق في الهواء. في المقابل، لا تمارس الأرض سوى سحب ضئيل لأسفل على حشرة ما. تعطينا تجاربنا اليومية أيضًا فكرة جيدة عن كيفية إضافة قوى متعددة. إذا دفع شخصان في اتجاهين مختلفين تجاه شخص ثالث، كما هو موضح في الشكل 5.3، فقد نتوقع أن تكون القوة الكلية في الاتجاه الموضح. نظرًا لأن القوة متجه، فإنها تُجمع تمامًا مثل المتجهات الأخرى. يتم تمثيل القوى، مثل المتجهات الأخرى، بواسطة الأسهم ويمكن إضافتها باستخدام طريقة الرأس إلى الذيل المألوفة أو الطرق المثلثية. تم تطوير هذه الأفكار في فصول المتجهات.

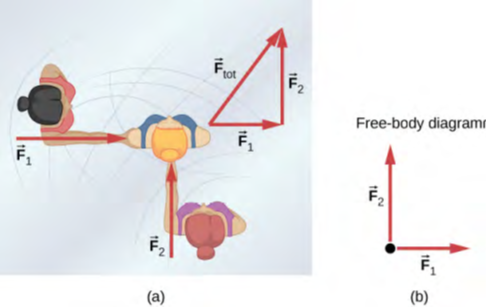
• الشكل 5.3 (a): القوى هي متجهات وتُجمع مثل المتجهات الأخرى، وبالتالي فإن القوة الكلية على المتزلج الثالث تكون في الاتجاه الموضح.
• الشكل 5.3 (b): رسم تخطيطي للجسم الحر يمثل القوى المؤثرة على المتزلج الثالث.

مخططات الجسم الحر

الشكل 5.3 (b) هو مثالنا الأول على مخطط الجسم الحر، وهو رسم تخطيطي يوضح جميع القوى الخارجية التي تؤثر على كائن أو نظام. يتم تمثيل الكائن أو النظام بنقطة واحدة معزولة (أو جسم حر)، ويتم عرض تلك القوى التي تؤثر عليه والتي تنشأ خارج الكائن أو النظام – أي القوى الخارجية -. (هذه القوى هي الوحيدة التي تظهر لأن القوى الخارجية فقط التي تؤثر على الجسم الحر تؤثر على حركته. يمكننا تجاهل أي قوى داخلية داخل الجسم). يتم تمثيل القوى بواسطة متجهات تمتد إلى الخارج من الجسم الحر.

تُعد مخططات الجسم الحر مفيدة في تحليل القوى التي تؤثر على كائن أو نظام، ويتم استخدامها على نطاق واسع في دراسة وتطبيق قوانين نيوتن للحركة. سوف تراهم في هذا الكتاب وفي جميع دراساتك للفيزياء. تشرح الخطوات التالية بإيجاز كيفية إنشاء مخطط الجسم الحر؛ ندرس هذه الاستراتيجية بمزيد من التفصيل في رسم مخططات الجسم الحر.

إستراتيجية حل مسائل قواني نيوتن للحركة

رسم مخططات الجسم الحر

1. ارسم الكائن قيد النظر. إذا كنت تتعامل مع الكائن على أنه جسيم، فقم بتمثيله كنقطة.

ضع هذه النقطة في أصل نظام إحداثيات س ص.

2. قم بتضمين جميع القوى التي تؤثر على الكائن، مع تمثيل هذه القوى كمتجهات. ومع ذلك، لا تقم بتضمين القوة الكلية على الكائن أو القوى التي يمارسها الكائن على بيئته.

3. حلل جميع متجهات القوة إلى مكوناتها في اتجاه س واتجاه ص.

4. ارسم مخططًا منفصلًا للجسم الحر لكل كائن في المسألة.

نوضح هذه الاستراتيجية مع مثالين لمخططات الجسم الحر (الشكل 5.4). سيتم شرح المصطلحات المستخدمة في هذا الشكل بمزيد من التفصيل لاحقًا في الفصل.

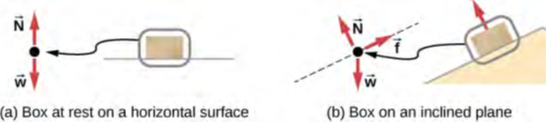
الشكل 5.4 في مخططات الجسم الحر هذه، N → هي القوة العادية، وW → هي وزن الجسم، وR → هي الاحتكاك.

الخطوات الواردة هنا كافية لإرشادك في استراتيجية حل مسائل قوانين نيوتن للحركة المهمة هذه. يوضح القسم الأخير من هذا الفصل بمزيد من التفصيل كيفية رسم مخططات الجسم الحر عند العمل بالأفكار المقدمة في هذا الفصل.

تطوير مفهوم القوة كمتجه

يمكن أن يعتمد التعريف الكمي للقوة على بعض القوة المعيارية، تمامًا كما تقاس المسافة بوحدات بالنسبة إلى الطول القياسي. أحد الاحتمالات هو مد الزنبرك مسافة ثابتة معينة (الشكل 5.5) واستخدام القوة التي يبذلها لسحب نفسه إلى شكله المريح – يسمى قوة الاستعادة – كمعيار. يمكن اعتبار حجم جميع القوى الأخرى بمثابة مضاعفات لهذه الوحدة القياسية للقوة. توجد العديد من الاحتمالات الأخرى للقوى القياسية. سيتم تقديم بعض التعريفات البديلة للقوة لاحقًا في هذا الفصل.

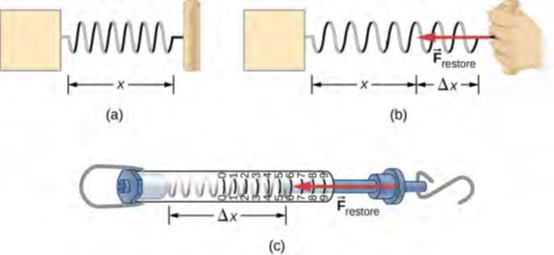
في الشكل 5.5، يمكن استخدام القوة التي يمارسها زنبرك ممتد كوحدة قياسية للقوة. (a) هذا الزنبرك يبلغ طوله x عندما يكون غير مشدود. (ب) عندما يمتد مسافة Δx، يمارس الزنبرك قوة استعادة F_restore →، وهي قابلة للتكرار. (c) مقياس الزنبرك هو أحد الأجهزة التي تستخدم زنبركًا لقياس القوة. يتم تطبيق القوة F_restore → على كل ما يتم توصيله بالخطاف. هنا، هذه القوة لها مقدار ست وحدات من معيار القوة المستخدمة.

تحليل القوى المؤثرة على جسم

دعونا نحلل القوة بشكل أعمق. لنفترض أن طالب فيزياء يجلس على طاولة ويعمل بجد على واجباته المنزلية (الشكل 5.6). ما القوى الخارجية التي تعمل عليه؟ هل يمكننا تحديد أصل هذه القوى؟

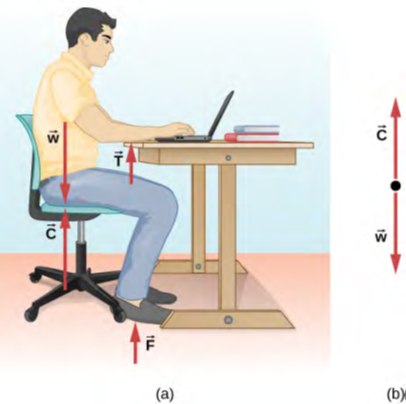
الشكل 5.6 (a) ترجع القوى المؤثرة على الطالب إلى الكرسي والطاولة والأرض وجاذبية الأرض. (b) عند حل مسألة تتعلق بالطالب، قد نرغب فقط في النظر في القوى المؤثرة على طول الخط الذي يمر عبر جذعه. يظهر رسم تخطيطي للجسم الحر لهذا الموقف.

فئات القوى

في معظم الحالات، يتم تجميع القوى في فئتين: قوى الاتصال وقوى المجال. كما قد تتخيل، فإن قوى الاتصال ناتجة عن الاتصال الجسدي المباشر بين الأشياء. على سبيل المثال، يواجه الطالب في الشكل 5.6 قوى التلامس C → و F → و T →، والتي يمارسها الكرسي على مؤخرته، والأرض على قدميه، والطاولة على ساعديه، على التوالي. ومع ذلك، تعمل قوى المجال دون الحاجة إلى الاتصال الجسدي بين الأشياء. إنها تعتمد على وجود “حقل” في منطقة الفضاء المحيطة بالجسم قيد الدراسة. نظرًا لأن الطالب في مجال الجاذبية الأرضية، فإنه يشعر بقوة الجاذبية w →؛ بعبارة أخرى، لديه وزن.

يمكنك التفكير في الحقل على أنه خاصية للفضاء يمكن اكتشافها بالقوى التي تمارسها. يعتقد العلماء أنه لا يوجد سوى أربعة مجالات قوة أساسية في الطبيعة. هذه هي مجالات الجاذبية والكهرومغناطيسية والنووية القوية والضعيفة (نعتبر هذه القوى الأربع في الطبيعة لاحقًا في هذا الكتاب). كما هو مذكور في w → في الشكل 5.6، فإن مجال الجاذبية مسؤول عن وزن الجسم. تشمل قوى المجال الكهرومغناطيسي قوى الكهرباء الساكنة والمغناطيسية؛ كما أنها مسؤولة عن التجاذب بين الذرات في المادة السائبة. كلا المجالين النوويين القوي والضعيف فعالان فقط على مسافات مساوية تقريبًا لطول مقياس لا يزيد عن نواة الذرة (10^-15 متر). مداها صغير جدًا بحيث لا يؤثر أي من المجالين في العالم الماكروسكوبي لميكانيكا نيوتن.

قوى الاتصال هي في الأساس كهرومغناطيسية. بينما يكون كوع الطالب في الشكل 5.6 ملامسًا لسطح الطاولة، تتفاعل الشحنات الذرية في جلده كهرومغناطيسيًا مع الشحنات الموجودة على سطح الطاولة. النتيجة الصافية (الإجمالية) هي القوة T →. وبالمثل، عندما يلتصق الشريط اللاصق بقطعة من الورق، تتداخل ذرات الشريط مع ذرات الورق لتسبب قوة كهرومغناطيسية صافية بين الجسمين. ومع ذلك، في سياق ميكانيكا نيوتن، فإن الأصل الكهرومغناطيسي لقوى الاتصال ليس مصدر اهتمام.

وحدة قياس القوة

كما ناقشنا سابقًا، القوة هي متجه؛ لها المقدار والاتجاه. تسمى وحدة القوة في النظام الدولي للوحدات بالنيوتن (والاختصار بالرمز N).

تعريف النيوتن

النيوتن N هي القوة اللازمة لتسريع جسم كتلته 1 كجم تسارغًا بمعدل 1 متر / ثانية ².

1 N = 1 kgm * m / c ^-2

1 نيوتن = 1 كجم * متر / ثانية ²

طريقة سهلة لتذكر مقدار النيوتن هي تخيل حمل تفاحة صغيرة؛ يبلغ وزنها حوالي 1 نيوتن.

يمكننا بالتالي وصف قوة ثنائية الأبعاد بالشكل التاي:

F → = ai ^ + bj ^

متجهات الوحدة i ^ و j ^ تشير إلى اتجاه هذه القوى على طول المحور x والمحور y، على التوالي.

كما يمكننا وصف القوة ثلاثية الأبعاد في الشكل التالي:

F → = ai ^ + bj ^ + ck ^

حساب محصلة القوى

في الشكل 5.3، لنفترض أن متزلج الجليد 1، على الجانب الأيسر من الشكل، يدفع أفقيًا بقوة 30.0 نيوتن إلى اليمين؛ نحن نمثل هذا كما يلي:

F → 1 = 30.0 i ^ N

وبالمثل، إذا دفع متزلج الجليد 2 بقوة 40.0 N في الاتجاه الرأسي الموجب الموضح في الشكل، فسنكتب:

F → 2 = 40.0j ^ N

تتسبب القوى في تسريع الكتلة – في هذه الحالة المتزلج – على الجليد بالاتجاه الثالث. يُطلق على هذا الناتج صافي القوة الخارجية F → _net ويتم إيجاده عن طريق أخذ المجموع الاتجاهي لجميع القوى الخارجية التي تؤثر على الكائن أو النظام (وبالتالي، يمكننا أيضًا تمثيل القوة الخارجية الصافية كـ Σ F →، حيث:

(5.1)

يمكن أن تمتد هذه المعادلة إلى أي عدد من القوى.

في هذا المثال، لدينا:

F → _net = Σ F → = F → 1 + F → 2 = 30.0i ^ + 40.0j ^ N

وتر المثلث الموضح في الشكل 5.3 هو القوة المحصلة، أو القوة الكلية Net Force. إنه متجه. لإيجاد مقداره (حجم المتجه، بغض النظر عن اتجاهه)، نستخدم القاعدة الواردة في المتجهات، بأخذ الجذر التربيعي لمجموع مربعات المكونات كما يلي:

أما الاتجاه فيتم تحديده كما يلي:

بالقياس من المحور السيني الموجب، كما هو موضح في الرسم التخطيطي للجسم الحر في الشكل 5.3 (ب).

مثال على مقدمة قوانين نيوتن للحركة

لنفترض أن المتزلجين على الجليد يدفعون الآن متزلج الجليد الثالث باستخدام:

→ F₁ = 3.0i ^ + 8.0j ^ N

و:

→ F₂ = 5.0i ^ + 4.0j ^ N

ما هي نتيجة هاتين القوتين؟ يجب أن ندرك أن القوة هي متجه؛ لذلك، يجب أن نجمع القوتين باستخدام قواعد جمع المتجهات:

تحقق من فهمك

أوجد مقدار واتجاه القوة الكلية في مثال متزلج الجليد المعطى أعلاه.

• لمعرفة كيفية جمع المتجهات راجع موضوع المتجهات – الكميات القياسية والكميات المتجهة.

المراجع

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022- 2023.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.