تحليل المتجهات والنظام الإحداثي الديكارتي

الملخص

تحليل المتجهات والنظام الإحداثي الديكارتي، شرح مفهوم تحليل المتجهات في بعدين وثلاثة أبعاد بدلالة مكوناتها باستخدام متجهات الوحدة على طول المحاور. طرق تحديد مقدار المتجه بدلالة مكوناته، تحديد زاوية الاتجاه للمتجه في المستوى. العلاقة بين الإحداثيات القطبية والإحداثيات الديكارتية في المستوى.

المحتويات

أهداف القسم:

بنهاية هذا القسم، سيكون القارئ قادرًا على:

تحليل المتجهات في بعدين وثلاثة أبعاد بدلالة مكوناتها، باستخدام متجهات الوحدة على طول المحاور.
التمييز بين مكونات المتجه والمكونات العددية للمتجه.
شرح كيف يتم تحديد مقدار المتجه من حيث مكونات المتجه.
تحديد زاوية الاتجاه للمتجه في المستوى.
شرح العلاقة بين الإحداثيات القطبية والإحداثيات الديكارتية في المستوى.

النظام الإحداثي الديكارتي

يتم تحليل المتجهات عادةً من حيث مكوناتها في نظام إحداثيات متعامدة. حتى في الحياة اليومية فإننا نستدعي بشكل طبيعي مفهوم الإسقاطات المتعامدة في نظام إحداثيات مستطيل. على سبيل المثال، إذا سألت شخصًا عن الاتجاهات إلى موقع معين، فمن المرجح أن يُطلب منك الذهاب 40 كم شرقًا و 30 كم شمالًا من 50 كم في الاتجاه 37 درجة شمال شرق.

في نظام الإحداثيات الديكارتي xy المستطيل في مستوى ما، يتم وصف نقطة في المستوى بزوج من الإحداثيات (x, y).

بطريقة مماثلة، يتم تحليل المتجه A⃗ في المستوى إلى زوج من إحداثيات المتجه. يُطلق على إحداثي x للمتجه A⃗ x المكون x الخاص بالمتجه، ويسمى إحداثي y للمتجه A⃗ المكون y الخاص به. المكوِّن المتجه x هو متجه يُشار إليه بـ A⃗ _x. المكوِّن المتجه y هو متجه يُشار إليه بـ A⃗ _y. في النظام الديكارتي، مكونات المتجه x و y للمتجه هي الإسقاطات المتعامدة لهذا المتجه على محوري x و y، على التوالي. بهذه الطريقة، باتباع قاعدة متوازي الأضلاع لجمع المتجهات، يمكن التعبير عن كل متجه على مستوى ديكارتي كمتجه المجموع لمكونات المتجه:

\vec{A} = {\vec{A}}_{x} + {\vec{A}}_{y} .

(2.10)

كما هو موضح في الشكل 2.16، المتجه A⃗ هو قطري المستطيل حيث يكون المكون A⃗ _x هو الجانب الموازي للمحور x والمكون A⃗ _y هو الجانب الموازي للمحور y. مكون المتجه A⃗ _x متعامد مع مكون المتجه A⃗ _y.

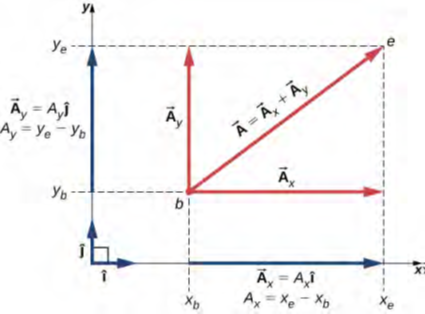
تحليل المتجهات والنظام الإحداثي الديكارتي – شكل 2.16

الشكل 2.16: المتجه A⃗ في مستوى في نظام الإحداثيات الديكارتية هو مجموع متجه لمكوني المتجه x و y. المكون المتجه A⃗ _x هو الإسقاط المتعامد للمتجه A⃗ على المحور x. المكون المتجه A⃗ _y هو الإسقاط المتعامد للمتجه A⃗ على المحور y. الأرقام A_x و A_y التي تضرب في متجهات الوحدة هي المكونات العددية للمتجه.

تحليل المتحهات بدلالة متجهات الوحدة

من المعتاد الإشارة إلى الاتجاه الموجب على المحور x بواسطة متجه الوحدة i^ والاتجاه الموجب على المحور y بواسطة متجه الوحدة j^. متجهات الوحدة للمحاور، i^ و j^، تحدد اتجاهين متعامدين في المستوى. كما هو موضح في الشكل 2.16، يمكن الآن كتابة المكونين x و y للمتجه بدلالة متجهات الوحدة للمحاور:

{\begin{matrix} {\vec{A}}_{x} = A_{x} \hat{i} \\ {\vec{A}}_{y} = A_{y} \hat{j} . \end{matrix}

(2.11)

المتجهات A⃗ _x و A⃗ _y المحددة بواسطة المعادلة 2.11 هي المكونات المتجهة للمتجه A⃗. الأرقام A_x و A_y التي تحدد مكونات المتجه في المعادلة 2.11 هي المكونات العددية للمتجه A⃗. بدمج المعادلة 2.10 مع المعادلة 2.11، نحصل على نموذج مكونات المتجه:

\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} .

(2.12)

إذا علمنا إحداثيات نقطة الأصل للمتجه b(xb, yb) حيث يشير b إلى “البداية Begining” والإحداثيات e(xe, ye) إلى نقطة نهاية المتجه، حيث يشير e إلى “النهاية End”، يمكننا الحصول على المكونات العددية للمتجه ببساطة عن طريق طرح إحداثيات نقطة الأصل من إحداثيات نقطة النهاية:

{\begin{matrix} A_{x} = x_{e} - x_{b} \\ A_{y} = y_{e} - y_{b} . \end{matrix}

(2.13)

مثال1: إزاحة مؤشر الماوس

يوجد مؤشر الماوس على شاشة العرض لجهاز الحاسوب في موضعه الأولي عند النقطة (6.0 سم، 1.6 سم) بالنسبة إلى الركن الأيسر السفلي. إذا قمت بتحريك المؤشر إلى رمز يقع عند النقطة (2.0 سم ، 4.5 سم)، فما متجه إزاحة المؤشر؟

إستراتيجية الحل

أصل نظام الإحداثيات xy هو الزاوية اليسرى السفلية لشاشة الحاسوب. لذلك، فإن متجه الوحدة i^ على المحور x يشير أفقيًا إلى اليمين ومتجه الوحدة j^ على المحور y يشير إلى عموديًا إلى الأعلى. يقع أصل متجه الإزاحة عند النقطة ب (6.0 ، 1.6) وتقع نهاية متجه الإزاحة عند النقطة هـ (2.0 ، 4.5). عوض بإحداثيات هذه النقاط في المعادلة 2.13 لإيجاد المكونين القياسيين D_x و D_y لمتجه الإزاحة D⃗. أخيرًا، استبدل الإحداثيات في المعادلة 2.12 لكتابة متجه الإزاحة في شكل مكونات المتجه.

الحل

نحدد x_b = 6.0 و x_e = 2.0 و y_b = 1.6 و y_e = 4.5 حيث تكون الوحدة المادية 1 سم. المكونات العددية x و y لمتجه الإزاحة هي:

\begin{matrix} D_{x} & = x_{e} - x_{b} = (2.0 - 6.0) cm = −4.0 cm, \\ D_{y} & = y_{e} - y_{b} = (4.5 - 1.6) cm = + 2.9 cm . \end{matrix}

شكل مكوّن المتجه لمتجه الإزاحة هو:

\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (−4.0 cm) \hat{i} + (2.9 cm) \hat{j} = (−4.0 \hat{i} + 2.9 \hat{j}) cm .

(2.14)

يظهر هذا الحل في الشكل 2.17:

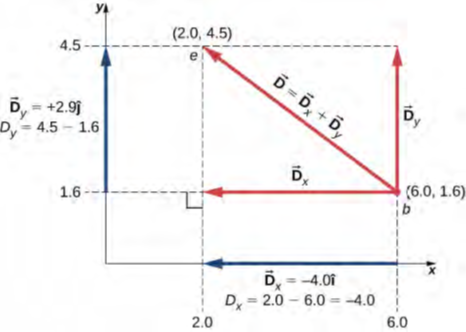
الشكل 2.17 الرسم البياني لمتجه الإزاحة. يشير المتجه من نقطة الأصل عند b إلى نقطة النهاية عند e.

الدلالة

لاحظ أن الوحدة المادية – هنا، 1 سم – يمكن وضعها إما مع كل مكون قبل متجه الوحدة مباشرة أو بشكل عام لكلا المكونين، كما في المعادلة 2.14. غالبًا ما تكون الطريقة الأخيرة أكثر ملاءمة لأنها أبسط.

المكون المتجه للمحور x هو: D⃗ x=−4.0iˆ=4.0(−iˆ) لمتجه الإزاحة له مقدار:

| {\vec{D}}_{x} | = | - 4.0 | | \hat{i} | = 4.0

لأن مقدار متجه الوحدة هو i ^ | = 1 |. لاحظ أيضًا أن اتجاه المكون x هو -i ^، وهو عكس اتجاه المحور x +؛ وبالتالي، يشير متجه المكون السيني D⃗_x إلى اليسار، كما هو موضح في الشكل 2.17. المكون السيني القياسي للمتجه D⃗هو D_x = −4.0.

وبالمثل، فإن المكون المتجه للمحورy هو D⃗_y = + 2.9^j^ لمتجه الإزاحة له مقدار:

| {\vec{D}}_{y} | = | 2.9 | | \hat{j} | = 2.9

لأن حجم متجه الوحدة هو j ^ | = 1 |. اتجاه المكون الصادي هو + j ^، وهو موازٍ لاتجاه المحور + y. لذلك، يشير متجه المكون y D → y لأعلى، كما هو موضح في الشكل 2.17. المكون y القياسي للمتجه D⃗ هو D_y = + 2.9. متجه الإزاحة D⃗ هو نتيجة مكوني المتجهين السيني والصادي.

يخبرنا شكل مكون المتجه لمعادلة متجه الإزاحة 2.14 أن مؤشر الماوس قد تم تحريكه على الشاشة بمقدار 4.0 سم إلى اليسار و2.9 سم لأعلى من موضعه الأولي.

تحقق من فهمك

ذبابة زرقاء تهبط على ورقة من ورق الرسم البياني عند نقطة تقع 10.0 سم على يمين حافتها اليسرى و8.0 سم فوق الحافة السفلية لها وتمشي ببطء إلى نقطة تقع على بعد 5.0 سم من الحافة اليسرى و5.0 سم من الحافة السفلية. اختر نظام الإحداثيات المستطيل مع الأصل في الزاوية السفلية اليسرى للورقة وابحث عن متجه الإزاحة للذبابة. وضح الحل الخاص بك عن طريق الرسوم البيانية.

مقدار المتجه وزاوية الاتجاه

عندما نعرف المركبين أو المكونين العدديين A_x و A_y للمتجه A⃗ باستخدام أسلوب تحليل المتجهات، يمكننا إيجاد مقداره A وزاوية اتجاهه θ_A. زاوية الاتجاه – أو الاتجاه باختصار – هي الزاوية التي يشكلها المتجه مع الاتجاه الموجب على المحور x.

يتم قياس الزاوية θ_A في اتجاه عكس عقارب الساعة من محور x الموجب إلى المتجه (الشكل 2.18). نظرًا لأن الأطوال A و A_x و A_y تشكل مثلثًا قائمًا، فهي مرتبطة بنظرية فيثاغورس:

A^{2} = A_{x}^{2} + A_{y}^{2} \Leftrightarrow A = \sqrt{A_{x}^{2} + A_{y}^{2}} .

(2.15)

تعمل هذه المعادلة حتى لو كانت المكونات أو المركبات العددية للمتجه سالبة. يتم تحديد زاوية الاتجاه θ_A للمتجه من خلال دالة الظل للزاوية θ_A في المثلث الموضح في الشكل 2.18:

tan θ = \frac{A_{y}}{A_{x}}

(2.16)

شكل زاوية المتجه

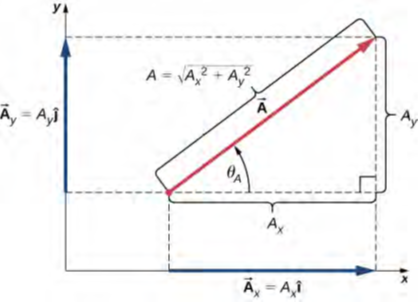
الشكل 2.18: عندما يقع المتجه إما في الربع الأول أو في الربع الرابع، حيث يكون المكون A_x موجبًا (الشكل 2.19)، تكون زاوية الاتجاه θ_A في المعادلة 2.16 مطابقة للزاوية θ

عندما يقع المتجه إما في الربع الأول أو في الربع الرابع، حيث يكون المكون A_x موجبًا (الشكل 2.19)، تكون الزاوية θ في المعادلة 2.16 مطابقة لزاوية الاتجاه θ_A. بالنسبة للمتجهات في الربع الرابع، تكون الزاوية سالبة، مما يعني أنه بالنسبة لهذه المتجهات، يتم قياس زاوية الاتجاه θ_A في اتجاه عقارب الساعة من المحور x الموجب. وبالمثل، بالنسبة للمتجهات في الربع الثاني، تكون الزاوية θ سالبة. عندما يقع المتجه في الربع الثاني أو الثالث، حيث يكون المحور المكون سالبًا، تكون زاوية الاتجاه θ_A = θ + 180 (الشكل 2.19).

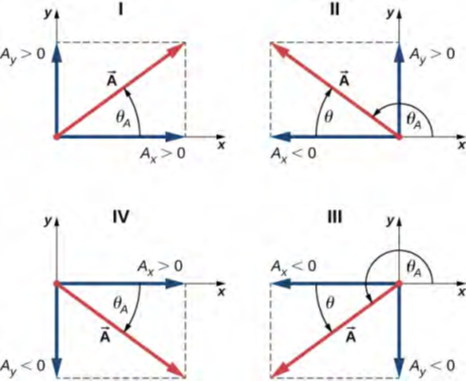
تحليل المتجهات والنظام الإحداثي الديكارتي – شكل 2.19

الشكل 2.19: قد تكون المكونات القياسية للمتجه موجبة أو سالبة. المتجهات في الربع الأول (I) لها كلا المكونين القياسيين أو المركبين القياسيين موجبين والمتجهات في الربع الثالث لها كلا المكونين القياسيين سالبين. بالنسبة إلى المتجهات في الربعين الثاني والثالث، تكون زاوية اتجاه المتجه θ_A = θ + 180 °.

مثال2: مقدار واتجاه متجه الإزاحة

يمكنك تحريك مؤشر الماوس على شاشة العرض من موضعه الأولي عند النقطة (6.0 سم، 1.6 سم) إلى رمز موجود عند النقطة (2.0 سم، 4.5 سم). ما مقدار واتجاه متجه إزاحة المؤشر؟

إستراتيجية الحل

في المثال السابق، وجدنا متجه الإزاحة D⃗ لمؤشر الماوس (انظر المعادلة 2.14)، وحددنا مكوناته العددية D_x = −4.0 cm و D_y = + 2.9 cm واستبدله في المعادلة 2.15 والمعادلة 2.16 لإيجاد المقدار D والاتجاه θ_D، على التوالي.

الحل

مقدار المتجه D⃗ هو:

D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{{(−4.0 cm)}^{2} + {(2.9 cm)}^{2}} = \sqrt{{(4.0)}^{2} + {(2.9)}^{2}} cm = 4.9 cm .

زاوية الاتجاه هي:

tan θ = \frac{D_{y}}{D_{x}} = \frac{+ 2.9 cm}{−4.0 cm} = −0.725 \Rightarrow θ = {tan}^{−1} (−0.725) = −35.9 ° .

يقع المتجه D⃗ في الربع الثاني، وبالتالي تكون زاوية اتجاهه:

θ_{D} = θ + 180 ° = −35.9 ° + 180 ° = 144.1 ° .

تحقق من فهمك

إذا كان متجه الإزاحة لذبابة زرقاء تسير على ورقة الرسم البياني هو:

\vec{D} = (−5.00 \hat{i} - 3.00 \hat{j}) cm

فأوجد مقدارها واتجاهها.

تطبيقات تحليل المتجهات

في العديد من التطبيقات، تُعرف مقادير واتجاهات كميات المتجهات ونحتاج إلى إيجاد ناتج العديد من المتجهات. على سبيل المثال، تخيل 400 سيارة تتحرك على جسر البوابة الذهبية في سان فرانسيسكو في وقت تهب فيه رياح قوية. تعطي كل سيارة للجسر دفعة مختلفة في اتجاهات مختلفة ونود أن نعرف مدى ضخامة الدفع الناتج. لقد اكتسبنا بالفعل بعض الخبرة في البناء الهندسي لمجموع المتجهات، لذلك نحن نعرف أن مهمة إيجاد النتيجة من خلال رسم المتجهات وقياس أطوالها وزواياها هي مهمة مستعصية على الحل السريع، مما يؤدي إلى أخطاء جسيمة، ولا تظهر مثل هذه المخاوف عند استخدامنا للطرق التحليلية. تتمثل الخطوة الأولى في النهج التحليلي في العثور على مكونات المتجه عندما يكون اتجاه وحجم المتجه معروفين.

لنعد إلى المثلث الأيمن في الشكل 2.18. حاصل قسمة الضلع المجاور A_x على الوتر A هو دالة جيب التمام لزاوية الاتجاه θ_A: A_x / A = cos θ_A، وحاصل قسمة الضلع المقابل A_y على الوتر A هو دالة الجيب لزاوية الاتجاه θ_A: A_y / A = sin θ_A، عندما يُعرف المقدار A والاتجاه θ_A، يمكننا حل هذه العلاقات للمكونات العددية:

{\begin{matrix} A_{x} = A cos θ_{A} \\ A_{y} = A sin θ_{A} \end{matrix} .

(2.17)

عند حساب مكونات المتجه باستخدام المعادلة 2.17، يجب توخي الحذر مع الزاوية. زاوية الاتجاه θ_A للمتجه هي الزاوية المقاسة عكس اتجاه عقارب الساعة من الاتجاه الموجب على المحور x للمتجه. قياس اتجاه عقارب الساعة يعطي زاوية سالبة.

مثال 3: تحليل المتجهات وتحديد مكونات متجه الإزاحة

حملة إنقاذ لطفل مفقود تتبع كلب بحث يُدعى “تروبر”. يتجول تروبر كثيرًا ويقوم بإجراء العديد من عمليات الاستنشاق التجريبية على طول العديد من المسارات المختلفة. في النهاية، وجد تروبر الطفل وكانت للقصة نهاية سعيدة، ولكن يبدو أن إزاحته على أرجل مختلفة معقد حقًا. يمشي على إحدى ساقيه مسافة 200.0 متر جنوب شرق، ثم يجري شمالاً حوالي 300.0 متر. في المحطة الثالثة، يفحص الروائح بعناية لمسافة 50.0 مترًا في اتجاه 30 درجة غربًا من الشمال. في المرحلة الرابعة، يتجه تروبر جنوبًا مباشرة لمسافة 80.0 مترًا، ويلتقط رائحة منعشة ويتحول إلى 23 درجة غربًا جنوبًا لمسافة 150.0 مترًا. باستخدام تحليل المتجهات في النظام الديكارتي، أوجد المكونات أو المركبات العددية لمتجهات الإزاحة لدى تروبر ومتجهات الإزاحة في شكل مكون متجه لكل ساق.

إستراتيجية الحل

دعونا نتبنى نظام إحداثيات مستطيل مع المحور x الموجب في اتجاه الشرق الجغرافي، مع توجيه الاتجاه y الموجب إلى الشمال الجغرافي. بشكل صريح، متجه الوحدة i ^ لنقاط المحور x شرقًا ومتجه الوحدة j ^ للمحور y يشير إلى الشمال. يصنع تروبر خمسة أرجل، لذلك هناك خمسة متجهات إزاحة، نبدأ بتحديد مقاديرها وزوايا اتجاهها، ثم نستخدم المعادلة 2.17 لإيجاد المكونات العددية للإزاحة والمعادلة 2.12 لإيجاد متجهات الإزاحة.

الحل

الجزء الأول أو المرحلة الأولى

في الجزء الأول مقدار الإزاحة L₁ = 200.0 m والاتجاه جنوبي شرقي. بالنسبة لزاوية الاتجاه θ₁، يمكننا قياس 45 درجة في اتجاه عقارب الساعة من الاتجاه الشرقي أو قياس 45 درجة + 270 درجة في عكس اتجاه عقارب الساعة من الاتجاه الشرقي. مع الاختيار الأول، θ₁ = −45 درجة. مع الاختيار الثاني، θ₁ = + 315 درجة. يمكننا استخدام إحدى هاتين الزاويتين. المكونات هي:

\begin{array}{l} L_{1 x} = L_{1} cos θ_{1} = (200.0 m) cos 315 ° = 141.4 m, \\ L_{1 y} = L_{1} sin θ_{1} = (200.0 m) sin 315 ° = −141.4 m . \end{array}

متجه الإزاحة للجزء الأول هو:

{\vec{L}}_{1} = L_{1 x} \hat{i} + L_{1 y} \hat{j} = (141.4 \hat{i} - 141.4 \hat{j}) m .

الجزء الثاني أو المرحلة الثانية

في الجزء الثاني من رحلات تروبر، مقدار الإزاحة هو L₂ = 300.0 م والاتجاه شمالًا. زاوية الاتجاه هي θ₂ = + 90 درجة. نحن نحصل على النتائج التالية:

\begin{matrix} L_{2 x} & = & L_{2} cos θ_{2} = (300.0 m) cos 90 ° = 0.0, \\ L_{2 y} & = & L_{2} sin θ_{2} = (300.0 m) sin 90 ° = 300.0 m, \\ {\vec{L}}_{2} & = & L_{2 x} \hat{i} + L_{2 y} \hat{j} = (300.0 m) \hat{j} . \end{matrix}

الجزء الثالث أو المرحلة الثالثة

في الجزء الثالث، حجم الإزاحة هو L₃ = 50.0 م والاتجاه 30 درجة غربًا من الشمال. زاوية الاتجاه المقاسة عكس اتجاه عقارب الساعة من الاتجاه الشرقي هي θ3 = 30 درجة + 90 درجة = + 120 درجة. هذا يعطي الإجابات التالية:

\begin{matrix} L_{3 x} & = & L_{3} cos θ_{3} = (50.0 m) cos 120 ° = −25.0 m, \\ L_{3 y} & = & L_{3} sin θ_{3} = (50.0 m) sin 120 ° = + 43.3 m, \\ {\vec{L}}_{3} & = & L_{3 x} \hat{i} + L_{3 y} \hat{j} = (−25.0 \hat{i} + 43.3 \hat{j}) m . \end{matrix}

الجزء الرابع أو المرحلة الرابعة

في الجزء الرابع من الرحلة، مقدار الإزاحة هو L₄ = 80.0 م والاتجاه جنوبًا. يمكن اعتبار زاوية الاتجاه إما θ₄ = −90 درجة أو θ₄ = + 270 درجة. نحصل على:

\begin{matrix} L_{4 x} & = & L_{4} cos θ_{4} = (80.0 m) cos (−90 °) = 0, \\ L_{4 y} & = & L_{4} sin θ_{4} = (80.0 m) sin (−90 °) = −80.0 m, \\ {\vec{L}}_{4} & = & L_{4 x} \hat{i} + L_{4 y} \hat{j} = (−80.0 m) \hat{j} . \end{matrix}

الجزء الخامس أو المرحلة الخامسة

في الجزء الأخير، مقدار الإزاحة هو L₅ = 150.0 m والزاوية θ₅ = – 23 ° + 270 ° = + 247 ° (23 ° غرب الجنوب)، مما يعطي:

\begin{matrix} L_{5 x} & = & L_{5} cos θ_{5} = (150.0 m) cos 247 ° = −58.6 m, \\ L_{5 y} & = & L_{5} sin θ_{5} = (150.0 m) sin 247 ° = −138.1 m, \\ {\vec{L}}_{5} & = & L_{5 x} \hat{i} + L_{5 y} \hat{j} = (−58.6 \hat{i} - 138.1 \hat{j}) m . \end{matrix}

تحقق من فهمك

إذا ركض تروبر 20 مترًا غربًا قبل أخذ قسط من الراحة، فما هو متجه الإزاحة؟

موضوع مقترح: المتجهات – الكميات القياسية والكميات المتجهة

المصدر

موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2022.
كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.