القوة الجاذبة المركزية

القوة الجاذبة المركزية

أهداف تعلم موضوع  القوة الجاذبة المركزية:

بنهاية هذا القسم، ستكون قادرًا على:

• شرح معادلة تسارع القوة الجاذبة المركزية
• تطبيق قانون نيوتن الثاني لتطوير معادلة القوة الجاذبة المركزية
• استخدم مفاهيم الحركة الدائرية في حل المسائل التي تتضمن قوانين نيوتن للحركة

في الحركة ثنائية وثلاثية الأبعاد، قمنا بفحص المفاهيم الأساسية للحركة الدائرية. يجب أن يكون الجسم الذي يمر بحركة دائرية، مثل إحدى سيارات السباق الموضحة في بداية هذا الفصل، متسارعًا لأنه يغير اتجاه سرعته. أثبتنا أن هذا التسارع الموجه مركزيًا، والذي يسمى تسارع الجاذبية المركزية، يتم الحصول عليه من خلال الصيغة التالية:

a _c = v² / r

حيث v هي سرعة الجسم، موجهة على طول خط مماس للمنحنى في أي لحظة. إذا عرفنا السرعة الزاوية ω، فيمكننا استخدامها:

a _c = r ω²

 تعطي السرعة الزاوية المعدل الذي يدور به الجسم خلال المنحنى بوحدة راديان / ث. يعمل هذا التسارع على طول نصف قطر المسار المنحني ويشار إليه أيضًا بالتسارع الشعاعي.

يجب أن يتم إنتاج التسارع بواسطة قوة. يمكن لأي قوة أو مجموعة من القوى أن تسبب تسارعًا جذريًا أو شعاعيًا. بعض الأمثلة هي التوتر في الحبل على كرة حبل، وقوة جاذبية الأرض على القمر، والاحتكاك بين الزلاجات الدوارة وأرضية حلبة التزلج، وقوة الطريق المنحنية على سيارة، والقوى المؤثرة على أنبوب جهاز طرد مركزي دوار.

أي قوة محصلة تسبب حركة دائرية منتظمة تسمى القوة الجاذبة المركزية Centripetal Force. اتجاه القوة الجاذبة نحو مركز الانحناء، وهو نفس اتجاه عجلة الجاذبية المركزية. وفقًا لقانون نيوتن الثاني للحركة، فإن صافي القوة هو التسارع ضرب الكتلة: F_net = ma.

بالنسبة للحركة الدائرية المنتظمة، يكون التسارع هو تسارع الجاذبية: a = a_c.

وهكذا، فإن مقدار القوة الجاذبة المركزية F_c يكون:

F_c = m a_c

بالتعويض عن تعبيرات عجلة الجاذبية المركزية a_{c :} (a_c = v²/r و a_c = rω²)، نحصل على تعبيرين للقوة الجاذبة المركزية Fc بدلالة الكتلة والسرعة وكذلك السرعة الزاوية ونصف قطر الانحناء:

F_c = mv² / r

 F_c = mrω²

(6.3)

يمكنك استخدام أي تعبير أكثر ملاءمة للقوة الجاذبة المركزية. القوة الجاذبة F _c تكون دائمًا عمودية على المسار وتشير إلى مركز الانحناء، لأن a_c عمودي على السرعة ويشير إلى مركز الانحناء. لاحظ أنك إذا قمت بحل أو إعادة كتابة التعبير الأول بالنسبة لـ r، فستحصل على:

r = m v² / F_c

 هذا يعني أنه بالنسبة لكتلة وسرعة معينة، فإن القوة الجاذبة المركزية الكبيرة تسبب نصف قطر صغير من الانحناء – أي، منحنى ضيق، كما في الشكل 6.20.

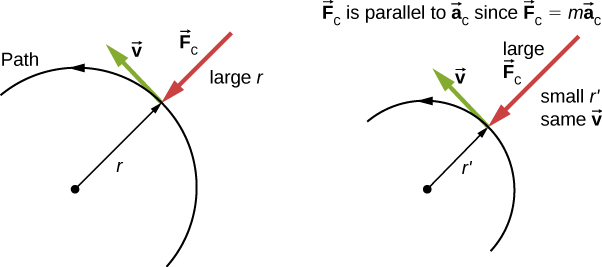
شكل 6.20: توفر قوة الاحتكاك قوة الجذب المركزية وتساويها عدديًا. القوة الجاذبة المركزية عمودية على السرعة وتسبب حركة دائرية منتظمة. كلما كانت F_c أكبر، كان نصف قطر الانحناء r أصغر وكان المنحنى أكثر حدة. المنحنى الثاني له نفس v، لكن F أكبر تنتج r أصغر.

مثال 6.15: ما معامل الاحتكاك الذي تحتاجه السيارات على منحنى مسطح؟

(أ) احسب القوة الجاذبة المركزية المؤثرة على سيارة وزنها 900.0 كجم وتجتاز منحنى نصف قطره 500.0 م عند 25.00 م / ث. (ب) بافتراض وجود منحنى غير مترابط، أوجد الحد الأدنى لمعامل الاحتكاك الثابت بين الإطارات والطريق، حيث أن الاحتكاك الساكن هو السبب الذي يمنع السيارة من الانزلاق (الشكل 6.21).

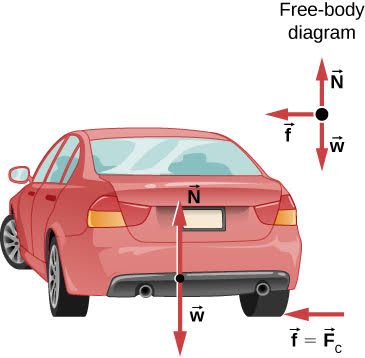
شكل 6.21: سيارة على أرض مستوية تتحرك بعيدًا وتتجه إلى اليسار. ترجع القوة الجاذبة المركزية التي تتسبب في دوران السيارة في مسار دائري إلى الاحتكاك بين الإطارات والطريق. مطلوب حد أدنى من معامل الاحتكاك، وإلا ستتحرك السيارة في منحنى بنصف قطر أكبر وتترك الطريق.

استراتيجية الحل

(أ) نحن نعلم أن:

F_c = mv² / r

وهكذا، يكون:

F_c=mv² / r = (900.0 kg)(25.00 m/s)² / (500.0 m) = 1125 N

(ب) يوضح الشكل 6.21 القوى المؤثرة على السيارة على منحنى (أرض مستوية)، يكون الاحتكاك جهة اليسار، مما يمنع السيارة من الانزلاق. ولأنها القوة الأفقية الوحيدة المؤثرة على السيارة، فإن الاحتكاك هو القوة الجاذبة المركزية في هذه الحالة. نحن نعلم أن الحد الأقصى للاحتكاك الساكن (الذي تتدحرج فيه الإطارات ولا تنزلق) هو: μ_sN، حيث μ_s هو معامل الاحتكاك الساكن وN هي القوة العادية. القوة العادية تساوي وزن السيارة على الأرض المستوية، لذا N = mg. وبالتالي فإن القوة الجاذبة المركزية في هذه الحالة هي:

F_c ≡ f = μ_s N = μ_s m g

الآن لدينا علاقة بين القوة الجاذبة المركزية ومعامل الاحتكاك. باستخدام المعادلة:

F_c = m v² / r

نحصل على:

m v² / r  = μ_s m g

بحل هذه المعادلة بالنسبة لـ μ_s، مع إلغاء الكتلة من طرفي المعادلة، نحصل على:

μ_s = v² / r g

 بالتعويض عن القيم المعلومة، نحصل على:

μ_s = (25.00 m/s)²/(500.0 m)(9.80 m/s²) = 0.13

(نظرًا لأن معاملات الاحتكاك تقريبية، فإن الإجابة تعطى لرقمين عشريين فقط).

الدلالة

معامل الاحتكاك الموجود في الشكل 6.21 (ب) أصغر بكثير مما هو موجود عادة بين الإطارات والطرق. لا تزال السيارة تتعامل على المنحنى إذا كان المعامل أكبر من 0.13، لأن الاحتكاك الساكن هو قوة استجابة قادرة على تحمل قيمة أقل من μ_sN ولكن ليس أكثر. سيسمح المعامل الأعلى للسيارة بالتعامل مع المنحنى بسرعة أعلى، ولكن إذا كان معامل الاحتكاك أقل، فإن السرعة الآمنة ستكون أقل من 25 م / ث. لاحظ أن الكتلة تلغي، مما يعني أنه، في هذا المثال، لا يهم مقدار الحمولة الثقيلة للسيارة للتعامل مع المنحنى. تلغي الكتلة لأن الاحتكاك يُفترض أنه متناسب مع القوة الطبيعية، والتي بدورها تتناسب مع الكتلة. إذا كان سطح الطريق ممدودًا، فستكون القوة الطبيعية أكبر، كما سوف نناقش لاحقًا.

تحقق من فهمك 6.9

سيارة تسير بسرعة 96.8 كم / ساعة تتحرك حول منحنى دائري نصف قطره 182.9 مترًا على طريق ريفي مسطح. ما هو الحد الأدنى لمعامل الاحتكاك الساكن لمنع السيارة من الانزلاق؟

المنحنيات المائلة (غير المستوية)

لنأخذ الآن في الاعتبار المنحنيات المائلة أو غير المستوية Banked Curves، حيث يساعدك انحدار الطريق على تجاوز المنحنى (الشكل 6.22). كلما زادت الزاوية θ، زادت سرعة أخذ المنحنى. غالبًا ما تحتوي مسارات السباق للدراجات وكذلك السيارات، على سبيل المثال، على منحنيات شديدة الانحدار. في “منحنى مائل بشكل مثالي”، تكون الزاوية بحيث يمكنك التعامل مع المنحنى بسرعة معينة دون مساعدة الاحتكاك بين الإطارات والطريق. سنشتق تعبيرًا لـ المنحنى المائل بشكل مثالي ونأخذ في الاعتبار مثالًا متعلقًا به.

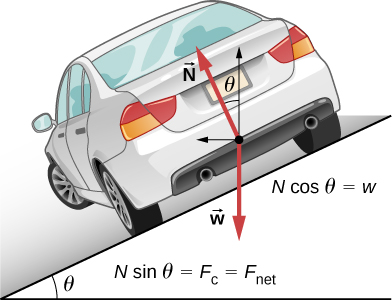
شكل 6.22: تتحرك السيارة على هذا المنحنى المتجه بعيدًا وتتجه إلى اليسار.

بالنسبة للميل المثالي، فإن صافي القوة الخارجية يساوي القوة الجاذبة المركزية الأفقية في حالة عدم وجود احتكاك. يجب أن تكون مكونات القوة العمودية N في الاتجاهين الأفقي والرأسي مساوية للقوة الجاذبة المركزية ووزن السيارة، على التوالي. في الحالات التي لا تكون فيها القوى متوازية، يكون من الأنسب النظر في المكونات على طول المحاور المتعامدة – في هذه الحالة، الاتجاهان الرأسي والأفقي.

يوضح الشكل 6.22 مخططًا للجسم الحر لسيارة على منحنى مائل بدون احتكاك. إذا كانت الزاوية θ مثالية للسرعة ونصف القطر، فإن صافي القوة الخارجية يساوي القوة الجاذبة المركزية اللازمة. القوتان الخارجيتان الوحيدتان اللتان تؤثران على السيارة هما وزنها والقوة الطبيعية للطريق N. (لا يمكن للسطح الخالي من الاحتكاك أن يبذل سوى قوة عمودية على السطح – أي قوة عادية). يجب أن يتم جمع هاتان القوتان لإعطاء قوة خارجية صافية أفقية باتجاه مركز الانحناء ولها المقدار mv² / r. نظرًا لأن هذه هي القوة الحرجة وهي أفقية، فإننا نستخدم نظام إحداثيات بمحاور رأسية وأفقية. فقط القوة العمودية لها مكون أفقي، لذلك يجب أن تساوي القوة الجاذبة المركزية، أي أن:

N sin θ = mv² / r

 نظرًا لأن السيارة لا تغادر سطح الطريق، يجب أن يكون صافي القوة الرأسية صفرًا، مما يعني أن المكونات الرأسية للقوتين الخارجيتين يجب أن تكون متساوية في المقدار ومتعاكسة في الاتجاه. من الشكل 6.22، نرى أن المكون الرأسي للقوة العمودية هو N cos θ، والقوة العمودية الأخرى الوحيدة هي قوة وزن السيارة. يجب أن تكون متساوية في المقدار؛ وهكذا يكون:

N cos θ = m g

 يمكننا الآن تجميع هاتين المعادلتين للتخلص من N والحصول على تعبير للزاوية θ حسب الاحتياج. بحل المعادلة الثانية لـ N = m g / (cosθ) واستبدال هذا في المعادلة الأولى، ينتج لنا:

mg (sin θ / cos θ) = m v ² / r

m g tan θ = m v² / r

tan θ = v² / r g

وبأخذ معكوس الظل، ينتج لنا:

Θ = tan⁻¹ (v² / r g)

(6.4)

يمكن فهم هذا التعبير من خلال النظر في كيفية اعتماد θ على v و r. يتم الحصول على θ كبير من أجل v كبير وr صغير. وهذا يعني أنه يجب أن تكون الطرق مائلة بشدة للحصول على سرعات عالية ومنحنيات حادة. يساعد الاحتكاك، لأنه يسمح لك بأخذ المنحنى بسرعة أكبر أو أقل مما لو كان المنحنى عديم الاحتكاك. لاحظ أن θ لا تعتمد على كتلة السيارة.

مثال 6.16: ما هي السرعة المثالية لأخذ منحنى ضيق شديد الانحدار؟

المنحنيات في بعض مسارات الاختبار ودورات السباق، مثل دايتونا إنترناشونال سبيدواي في فلوريدا، هي منحنيات شديدة الانحدار. تسمح هذه العملية المائلة، بمساعدة احتكاك الإطارات وتكوينات السيارة المستقرة للغاية، بأخذ المنحنيات بسرعة عالية جدًا. للتوضيح، احسب السرعة التي ينبغي عندها دفع سيارة تسير في منحنى بنصف قطر يبلغ 100 متر مائل بزاوية 31.0 درجة إذا كان الطريق عديم الاحتكاك.

استراتيجية الحل

نلاحظ أولاً أن جميع الشروط في التعبير عن الزاوية المثالية لمنحنى متداول باستثناء السرعة هي معروفة؛ لذلك، نحتاج فقط إلى إعادة ترتيبها بحيث تظهر السرعة على الجانب الأيسر ثم نعوض بالكميات المعروفة.

الحل

نبدأ بـ:

tan θ = v² / r g

نحصل على:

مع ملاحظة أن tan 31.0 ° = 0.609

نحصل على:

الدلالة

هذا فقط حوالي 165 كم / ساعة، بما يتوافق مع منحنى شديد الانحدار وحاد إلى حد ما. يمكّن احتكاك إطارات السيارة من الانحناء بسرعات أعلى بكثير.

تحليل حركة الطائرات المائلة

تقوم الطائرات بالحركات الدورانية عن طريق الميل. قوة الرفع، بسبب قوة الهواء على الجناح، تعمل بزاوية قائمة على الجناح. عندما تكون الطائرة مائلة، يحصل الطيار على رفع أكبر من اللازم لتحليق الطائرة للأعلى. يوازن المكون الرأسي للرفع وزن الطائرة، ويعمل المكون الأفقي على تسريع الطائرة. تُعطى زاوية الميل الموضحة في الشكل 6.23 بواسطة θ. نقوم بتحليل القوى بنفس الطريقة التي نتعامل بها مع حالة السيارة التي تدور حول منحنى مائل.

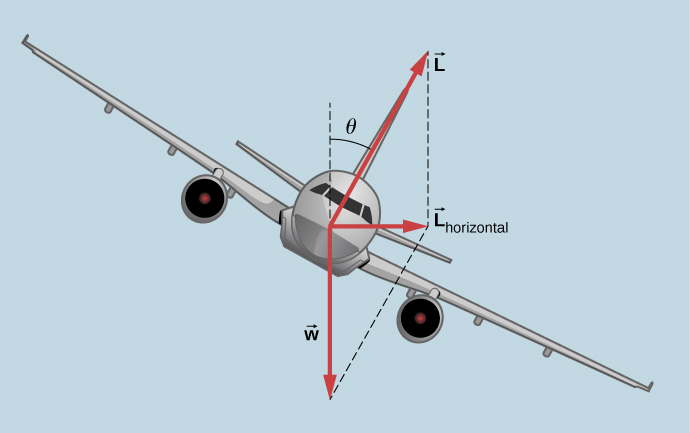
الشكل 6.23: في المنحنى المائل، يكون المكون الأفقي للرفع غير متوازن ويسرع الطائرة. يوازن المكون الطبيعي للرافعة وزن الطائرة. زاوية الميل مُعطاة بـ θ. قارن مخطط المتجه مع الرسم الموضح في الشكل 6.22.

تفاعلي

انضم إلى الخنفساء في استكشاف الحركة الدورانية. قم بتدوير الدوامة لتغيير زاويتها أو اختيار سرعة زاويّة ثابتة أو تسارع زاوية. اكتشف كيف ترتبط الحركة الدائرية بالموضع xy للخطأ وسرعته وتسارعه باستخدام المتجهات أو الرسوم البيانية.

تفاعلي

تتطلب الحركة الدائرية قوة، تسمى القوة الجاذبة المركزية، والتي يتم توجيهها إلى محور الدوران. يوضح هذا النموذج المبسط للدائرة هذه القوة.

القصور الذاتي والإطارات (المتسارعة): قوة كوريوليس

ما الذي يشترك فيه الإقلاع في طائرة نفاثة، والانعطاف في زاوية في السيارة، وركوب الخيل، والحركة الدائرية للإعصار المداري؟ يُظهر كل قوى قصور ذاتي – قوى يبدو أنها تنشأ فقط من الحركة، لأن الإطار المرجعي للمراقب يتسارع أو يدور. عند الإقلاع على متن طائرة، يتفق معظم الناس على الشعور كما لو أنك دفعت مرة أخرى إلى المقعد بينما تتسارع الطائرة على المدرج. ومع ذلك، قد يقول الفيزيائي أنك تميل إلى البقاء ثابتًا بينما يدفعك المقعد للأمام. تحدث تجربة أكثر شيوعًا عندما تقوم بعمل منحنى ضيق في سيارتك – على سبيل المثال، إلى اليمين (الشكل 6.24). تشعر كما لو أنك أُلقيت (أي مجبرًا) على اليسار بالنسبة للسيارة. مرة أخرى، قد يقول الفيزيائي أنك تسير في خط مستقيم (تذكر قانون نيوتن الأول) لكن السيارة تتحرك إلى اليمين، وليس أنك تواجه قوة من اليسار.

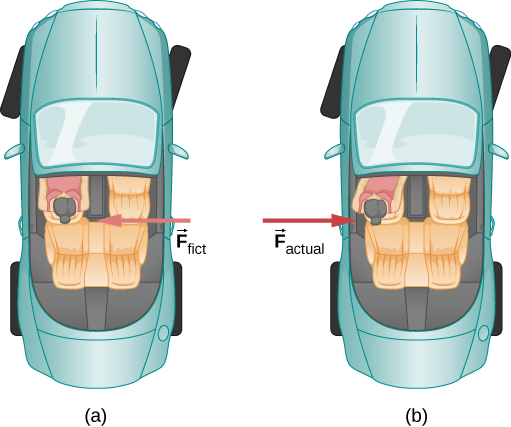
الشكل 6.24 (أ) يشعر سائق السيارة بنفسه مجبرًا على الميل ناحية اليسار بالنسبة للسيارة عندما تستدير هي إلى اليمين. هذه قوة بالقصور الذاتي تنشأ عن استخدام السيارة كإطار مرجعي. (ب) في الإطار المرجعي للأرض، يتحرك السائق في خط مستقيم، مطيعًا قانون نيوتن الأول، وتتحرك السيارة إلى اليمين. لا توجد قوة على اليسار على السائق بالنسبة إلى الأرض. بدلاً من ذلك، توجد قوة على اليمين على السيارة تجعلها تنعطف.

يمكننا التوفيق بين وجهات النظر هذه من خلال فحص الأطر المرجعية المستخدمة. دعونا نركز على الأشخاص في السيارة. يستخدم الركاب السيارة بشكل غريزي كإطار مرجعي، في حين أن الفيزيائي قد يستخدم الأرض كإطار مرجعي. قد يقوم الفيزيائي بهذا الاختيار لأن الأرض عبارة عن إطار مرجعي بالقصور الذاتي تقريبًا، حيث يكون لجميع القوى أصل مادي يمكن تحديده. في مثل هذا الإطار المرجعي، تأخذ قوانين نيوتن للحركة الشكل الوارد في قوانين نيوتن للحركة. السيارة عبارة عن إطار مرجعي لا يعمل بالقوة الذاتية لأنه يتم تسريعها إلى الجانب. القوة على اليسار التي يشعر بها ركاب السيارة هي قوة قصور ذاتي ليس لها أصل مادي (إنها ناتجة فقط عن خمول الراكب، وليس لسبب مادي مثل الشد أو الاحتكاك أو الجاذبية). السيارة والسائق يتسارعان في الواقع إلى جهة اليمين. يُقال إن قوة القصور الذاتي هذه هي قوة القصور الذاتي Inertial Force لأنها ليس لها أصل مادي، مثل الجاذبية.

سيختار الفيزيائي الإطار المرجعي الأكثر ملاءمة للموقف الذي يتم تحليله. لا توجد مشكلة للفيزيائي في تضمين قوى القصور الذاتي وقانون نيوتن الثاني، كالعادة، إذا كان ذلك أكثر ملاءمة، على سبيل المثال، في لعبة دوّارة أو على كوكب دوار. تُستخدم الأطر المرجعية غير الذاتية (المعجلة) عندما يكون من المفيد القيام بذلك. يجب أخذ أطر مرجعية مختلفة في الاعتبار عند مناقشة حركة رائد فضاء في مركبة فضائية تسافر بسرعات تقترب من سرعة الضوء، كما ستقدر في دراسة النظرية النسبية الخاصة.

مثال حركة دوران لعبة الملاهي

دعونا الآن نأخذ جولة ذهنية في جولة مرح – على وجه التحديد، ملعب مرح سريع الدوران (الشكل 6.25). أنت تأخذ لعبة Merry-go-round لتكون الإطار المرجعي الخاص بك لأنك تقوم بالتناوب معًا. عند الدوران في هذا الإطار المرجعي غير الذاتي، تشعر بقوة قصور ذاتي تميل إلى طردك؛ يُشار إلى هذا غالبًا باسم قوة الطرد المركزي (يجب عدم الخلط بينه وبين القوة الجاذبة المركزية). قوة الطرد المركزي Centrifugal Force هي مصطلح شائع الاستخدام، لكنها غير موجودة في الواقع. يجب عليك التمسك بإحكام لمواجهة القصور الذاتي (الذي يشير إليه الناس غالبًا باسم قوة الطرد المركزي). في الإطار المرجعي للأرض، لا توجد قوة تحاول طردك؛ نؤكد أن قوة الطرد المركزي خيال. يجب عليك التمسك بجعل نفسك تسير في دائرة لأنه بخلاف ذلك ستسير في خط مستقيم، بعيدًا عن لعبة الدوامة، بما يتماشى مع قانون نيوتن الأول. لكن القوة التي تمارسها تعمل تجاه مركز الدائرة.

في الشكل أ، عند النظر إلى الأسفل على دوامة، نرى طفلًا جالسًا على حصان يتحرك في اتجاه عكس عقارب الساعة مع أوميغا السرعة الزاوية. القوة F الفرعية تساوي قوة الطرد المركزي عند نقطة التلامس بين العمود الذي يحمل الحصان وسطح الدوران. القوة شعاعيًا إلى الخارج من مركز الدوامة. هذا هو الإطار المرجعي الدوار لمرحلة الدوامة. في الشكل ب، نرى الوضع في الإطار المرجعي بالقصور الذاتي. شوهد الطفل يدور بسرعة الزاوية أوميغا في اتجاه عكس عقارب الساعة. يظهر الطفل على الحصان في نفس الوضع كما في الشكل أ. القوة الكلية تساوي القوة الجاذبة امركزية، وتتجه شعاعيًا نحو المركز. في الظل، نظهر أيضًا للطفل في موضع سابق وفي الموضع الذي كان سيحصل عليه إذا كانت القوة الكلية عليه صفرًا، وهو مستقيم للأمام وبالتالي في نصف قطر أكبر من وضعه الفعلي.

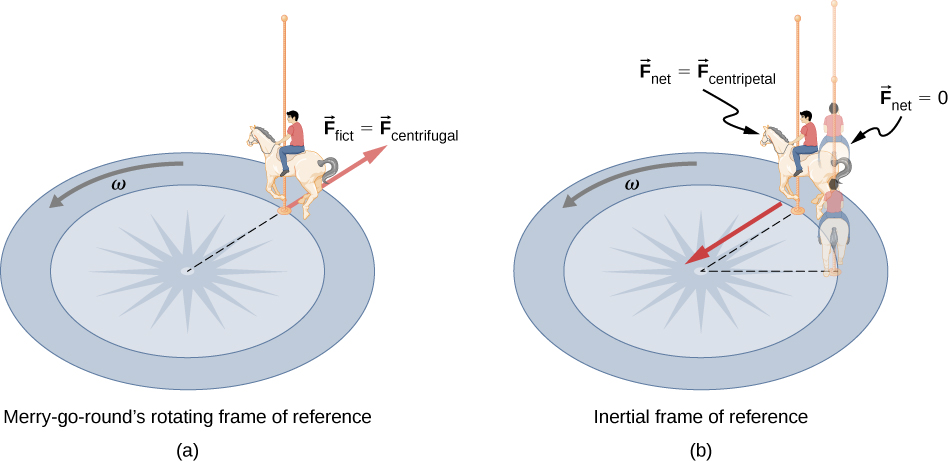
الشكل 6.25 (أ) يشعر المتسابق في لعبة الدوامة وكأنه قد تم دفعه للخارج. تسمى هذه القوة بالقصور الذاتي وعن طريق الخطأ أحيانًا يطلق عليها اسم قوة الطرد المركزي في محاولة لشرح حركة الفارس في الإطار المرجعي الدوار. (ب) في إطار مرجعي بالقصور الذاتي ووفقًا لقوانين نيوتن، فإن قصوره الذاتي هو الذي يحمّله (يمتلك الفارس غير المظلل F_net = 0 والرؤوس في خط مستقيم). هناك حاجة إلى قوة جاذبة F_centripetal لإحداث مسار دائري.

مثال أجهزة الطرد المركزي

هذا التأثير بالقصور الذاتي، الذي ينقلك بعيدًا عن مركز الدوران إذا لم تكن هناك قوة جاذبة مركزية للتسبب في حركة دائرية، يتم استخدامه بشكل جيد في أجهزة الطرد المركزي (الشكل 6.26). يدوّر جهاز الطرد المركزي العينة بسرعة كبيرة، كما ذكرنا سابقًا في هذا الفصل. بالنظر إلى الإطار المرجعي الدوار، فإن قوة القصور الذاتي ترمي الجسيمات إلى الخارج، مما يؤدي إلى تسريع عملية ترسيبها. كلما زادت السرعة الزاوية، زادت قوة الطرد المركزي. لكن ما يحدث حقًا هو أن القصور الذاتي للجسيمات يحملها على طول خط مماس للدائرة بينما يتم دفع أنبوب الاختبار في مسار دائري بواسطة القوة الجاذبة المركزية.

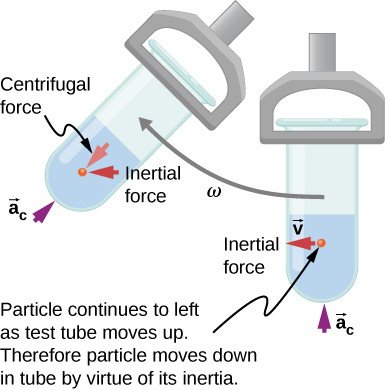
الشكل 6.26: تستخدم أجهزة الطرد المركزي القصور الذاتي لأداء مهمتها. تستقر الجسيمات الموجودة في الرواسب السائلة لأن قصورها الذاتي يحملها بعيدًا عن مركز الدوران. تعمل السرعة الزاوية الكبيرة لجهاز الطرد المركزي على تسريع عملية الترسيب. في النهاية، تتلامس الجسيمات مع جدران أنبوب الاختبار، والتي توفر بعد ذلك قوة الجاذبية المركزية اللازمة لجعلها تتحرك في دائرة نصف قطرها ثابت.

دعونا الآن نفكر فيما يحدث إذا تحرك شيء ما في إطار مرجعي دوار. على سبيل المثال، ماذا لو حركت كرة بعيدًا مباشرةً عن مركز لعبة الدوامة، كما هو موضح في الشكل 6.27؟ تتبع الكرة مسارًا مستقيمًا بالنسبة إلى الأرض (بافتراض احتكاك ضئيل) ومسار منحني إلى اليمين على سطح الكرة الدوارة. الشخص الذي يقف بجانب الدوامة يرى الكرة تتحرك بشكل مستقيم بينما تدور الدوامة أسفلها. في الإطار المرجعي للدوران المائل، نشرح المنحنى الظاهر إلى اليمين باستخدام قوة قصور ذاتية، تسمى قوة كوريوليس، والتي تجعل الكرة تنحني إلى اليمين. يمكن استخدام قوة كوريوليس من قبل أي شخص في هذا الإطار المرجعي لشرح سبب اتباع الكائنات لمسارات منحنية وتسمح لنا بتطبيق قوانين نيوتن في إطارات مرجعية غير ذاتية.

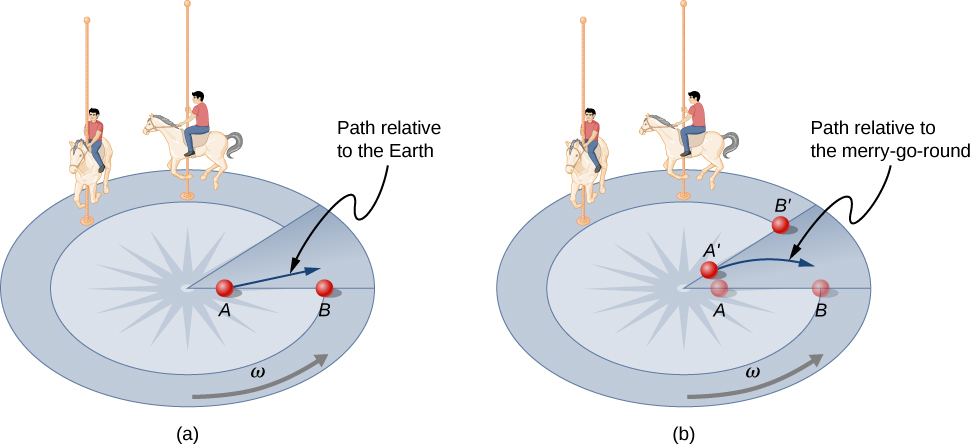
الشكل 6.27: بالنظر إلى الدوران في عكس اتجاه عقارب الساعة لدوامة دائرية، نرى أن الكرة تنزلق بشكل مستقيم نحو الحافة وتتبع مسارًا منحنيًا إلى اليمين. يقوم الشخص بتحريك الكرة نحو النقطة B، بدءًا من النقطة A. تدور كلتا النقطتين إلى المواضع المظللة (A’و B’) الموضحة في الوقت الذي تتبع فيه الكرة المسار المنحني في الإطار الدوار والمسار المستقيم في إطار الأرض .

حتى الآن، اعتبرنا الأرض إطارًا مرجعيًا بالقصور الذاتي مع القليل من القلق أو لا داعي للقلق بشأن التأثيرات بسبب دورانها. ومع ذلك، فإن مثل هذه التأثيرات موجودة بالفعل – في دوران أنظمة الطقس، على سبيل المثال. يمكن فهم معظم عواقب دوران الأرض نوعيًا عن طريق القياس مع لعبة الدوامة. بالنظر من أعلى القطب الشمالي، تدور الأرض عكس اتجاه عقارب الساعة، كما تفعل الدوامة المرحة في الشكل 6.27. كما هو الحال في لعبة الدوامة، فإن أي حركة في نصف الكرة الشمالي للأرض تتعرض لقوة كوريوليس إلى اليمين. يحدث العكس تمامًا في نصف الكرة الجنوبي. هناك، القوة على اليسار. نظرًا لأن السرعة الزاوية للأرض صغيرة، فإن قوة كوريوليس عادةً ما تكون مهملة، ولكن بالنسبة للحركات واسعة النطاق، مثل أنماط الرياح، فإن لها تأثيرات كبيرة.

مثال دوران الأعاصير

تتسبب قوة كوريوليس في دوران الأعاصير في نصف الكرة الشمالي في اتجاه عكس اتجاه عقارب الساعة، بينما تدور الأعاصير المدارية في نصف الكرة الجنوبي في اتجاه عقارب الساعة. (تُعد مصطلحات الإعصار والدوامة والعاصفة الاستوائية أسماء إقليمية محددة للأعاصير، وهي أنظمة عاصفة تتميز بمراكز الضغط المنخفض والرياح القوية والأمطار الغزيرة). يساعد الشكل 6.28 على إظهار كيفية حدوث هذه الدورات. يتدفق الهواء نحو أي منطقة ذات ضغط منخفض، وتحتوي الأعاصير المدارية على ضغوط منخفضة بشكل خاص. وهكذا تتدفق الرياح باتجاه مركز الإعصار المداري أو نظام الطقس منخفض الضغط على السطح. في نصف الكرة الشمالي، تنحرف هذه الرياح الداخلية إلى اليمين، كما هو موضح في الشكل، مما ينتج عنه دوران في عكس اتجاه عقارب الساعة على السطح لمناطق الضغط المنخفض من أي نوع. يرتبط الضغط المنخفض على السطح بارتفاع الهواء، والذي ينتج أيضًا التبريد وتكوين السحب، مما يجعل أنماط الضغط المنخفض مرئية تمامًا من الفضاء. وعلى العكس من ذلك، فإن دوران الرياح حول مناطق الضغط المرتفع يكون في اتجاه عقارب الساعة في نصف الكرة الجنوبي ولكنه أقل وضوحًا لأن الضغط المرتفع مرتبط بكتم الهواء، مما ينتج عنه سماء صافية.

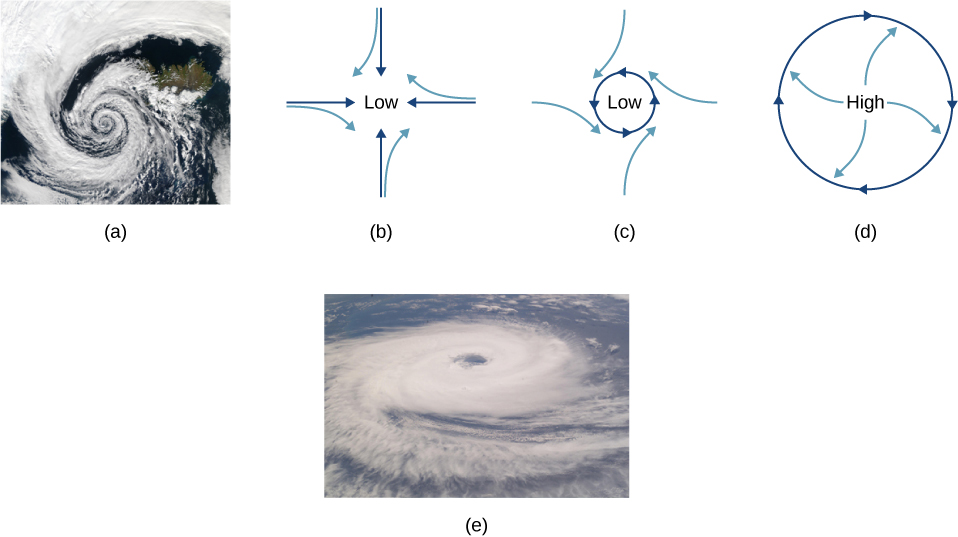
الشكل 6.28: (أ) يعد الدوران بعكس اتجاه عقارب الساعة لهذا الإعصار في نصف الكرة الشمالي نتيجة رئيسية لقوة كوريوليس. (ب) بدون قوة كوريوليس، سيتدفق الهواء مباشرة إلى منطقة الضغط المنخفض، مثل تلك الموجودة في الأعاصير المدارية. (ج) تعمل قوة كوريوليس على انحراف الرياح إلى اليمين، مما يؤدي إلى دوران في عكس اتجاه عقارب الساعة. (د) تنحرف الرياح المتدفقة بعيدًا عن منطقة الضغط المرتفع إلى اليمين أيضًا، مما ينتج عنه دوران في اتجاه عقارب الساعة. (هـ) يتم إنتاج الاتجاه المعاكس للدوران بواسطة قوة كوريوليس في نصف الكرة الجنوبي، مما يؤدي إلى الأعاصير المدارية. (المصدر: وكالة ناسا).

يمكن أيضًا تفسير دوران الأعاصير المدارية ومسار الكرة على لعبة الدوامة بالقصور الذاتي ودوران النظام الموجود تحتها. عند استخدام إطارات غير ذاتية، يجب اختراع قوى القصور الذاتي، مثل قوة كوريوليس، لشرح المسار المنحني. لا يوجد مصدر مادي يمكن تحديده لهذه القوى بالقصور الذاتي. في إطار القصور الذاتي، يشرح القصور الذاتي المسار، ولا توجد قوة بدون مصدر محدد. يسمح لنا كلا الرأيين بوصف الطبيعة، لكن النظرة في إطار القصور الذاتي هي أبسط من حيث أن جميع القوى لها أصول وتفسيرات.

المراجع

• موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، 2022.
• كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.