أهداف التعلم: بنهاية هذا القسم الخاص بموضوع القدرة ستكون قادرًا على:
- ربط الشغل المبذول خلال فترة زمنية بالطاقة المسلمة
- إيجاد القدرة الناتجة عن قوة مؤثرة على جسم متحرك
المحتويات
مفهوم القدرة
مفهوم الشغل ينطوي على القوة والإزاحة؛ تربط نظرية الشغل والطاقة صافي الشغل المبذول على الجسم بالاختلاف في طاقته الحركية، المحسوبة بين نقطتين على مساره. لا تتضمن أي من هذه الكميات أو العلاقات الوقت أو الزمن بشكل صريح، ومع ذلك فنحن نعلم أن الوقت المتاح لإنجاز قدر معين من الشغل غالبًا ما يكون بنفس أهمية مقدار الشغل نفسه. في الشكل الافتتاحي للفصل، قد يكون العديد من العدائين قد حققوا نفس السرعة في النهاية، وبالتالي قاموا بنفس القدر من الشغل، لكن الفائز بالسباق قام بذلك في أقل وقت ممكن.
نقوم بالتعبير عن العلاقة بين الشغل المبذول والفاصل الزمني الذي ينطوي عليه القيام به، من خلال تقديم مفهوم القدرة Power. نظرًا لأن الشغل يمكن أن يتغير كدالة للوقت، فإننا نحدد أولاً متوسط القدرة على أنه الشغل المنجز خلال فترة زمنية، مقسومًا على الفترة الزمنية:
7.10
بعد ذلك، يمكننا تحديد القدرة اللحظية (يشار إليها كثيرًا على أنها مجرد قدرة بسيطة).
تعريف القدرة
تُعرَّف القدرة بأنها معدل أداء الشغل، أو نهاية متوسط القدرة للفترات الزمنية التي تقترب من الصفر:
7.11
إذا كانت القدرة ثابتة على مدى فترة زمنية، فإن متوسط القدرة لتلك الفترة الزمنية يساوي القدرة اللحظية، والشغل الذي يقوم به العامل الذي يوفر القدرة هو W = PΔt. إذا اختلفت القدرة خلال فترة ما بمرور الوقت، فإن الشغل المبذول تكامل القدرة بالنسبة للزمن:
ترتبط نظرية الشغل والطاقة بكيفية تحويل الشغل إلى طاقة حركية. نظرًا لوجود أشكال أخرى من الطاقة أيضًا، كما نناقش في الفصل التالي، يمكننا أيضًا تعريف القدرة على أنها معدل نقل الطاقة. يُقاس الشغل والطاقة بوحدات الجول، لذلك تُقاس القدرة بوحدات الجول في الثانية، والتي تم إعطاؤها اسم وات Watt بالنظام الدولي للقياس SI، وبالاختصار W= 1J / s.
وحدة أخرى شائعة للتعبير عن القدرة للأجهزة الكهربائية في الحياة اليومية هي القدرة الحصانية، حيث يكون 1 حصان = 746 وات.
مثال 7.11: قدرة السحب
متدرب عسكري وزنه 80 كجم يقوم بعمليات سحب على شريط أفقي ( الشكل 7.14 ). يستغرق المتدرب 0.8 ثانية لرفع الجسم من الموضع السفلي إلى حيث تكون الذقن فوق العارضة. ما مقدار القدرة التي تزودها عضلات المتدرب بتحريك جسده من الموضع السفلي إلى مكان الذقن فوق العارضة؟ (تلميح: ضع تقديرات معقولة لأي كميات مطلوبة).
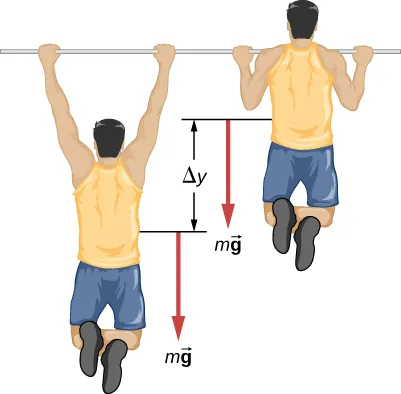
الشكل 7.14: ما هي القدرة المستهلكة في القيام بعشر عمليات سحب في عشر ثوانٍ؟
استراتيجية الحل
الشغل المبذول ضد الجاذبية، صعودًا أو هبوطًا مسافة Δy هي mg Δy. لنفترض أن Δy = ft≈60 cm. افترض أيضًا أن الذراعين تشكلان 10٪ من كتلة الجسم ولا تدخلان في الكتلة المتحركة. باستخدام هذه الافتراضات، يمكننا حساب الشغل المبذول.
الحل
النتيجة التي نحصل عليها، بتطبيق افتراضاتنا، هي:
الدلالة
هذا هو الحال بالنسبة لإنفاق القدرة في ممارسة شاقة؛ في وحدات القياس اليومية، إنها إلى حد ما أكثر من حصان واحد (1حصان = 746 وات).
تحقق من فهمك 7.8
احسب القدرة المنفقة بواسطة رافع أثقال يرفع قضيب حديد وزنه 150 كجم 2 متر في 3 ثوانٍ.
التعبير عن القدرة بدلالة القوة المؤثرة
يمكن أيضًا التعبير عن القدرة التي ينطوي عليها تحريك الجسم من حيث القوى المؤثرة عليه. إذا كانت القوة F تؤثر على جسم تم إزاحته مسافة dr في وقت dt، فإن القدرة التي تنفقها هذه القوة هي:
7.12
حيث v هي سرعة الجسم.
حقيقة أن النهاية التي تتضمنها المشتقات موجودة، لحركة جسم حقيقي، تبرر إعادة ترتيب اللامتناهيات في الصغر.
مثال 7.12: قدرة قيادة السيارات أعلى منحدر
ما مقدار القدرة التي يجب أن يبذلها محرك السيارة لتحريك سيارة تزن 1200 كجم إلى أعلى منحدر مائل بنسبة 15٪ عند 90 كم / ساعة ( الشكل 7.15 )؟ افترض أن 25٪ من هذه الطاقة تبدد للتغلب على مقاومة الهواء والاحتكاك.
الشكل 7.15: نريد حساب القدرة اللازمة لتحريك سيارة لأعلى التل بسرعة ثابتة.
استراتيجية الحل
عند السرعة الثابتة، لا يوجد أي تغيير في الطاقة الحركية، وبالتالي فإن صافي الشغل المبذول لتحريك السيارة يساوي صفرًا. لذلك فإن القدرة التي يوفرها المحرك لتحريك السيارة تساوي القدرة المنفقة ضد الجاذبية ومقاومة الهواء. من خلال الافتراض، يتم توفير 75٪ من القدرة مقابل الجاذبية، وهو ما يعادل:
حيث θ هي زاوية ميل المنحدر. تعني الدرجة 15٪ أن θ = 0.15.
هذا المنطق يسمح لنا بإيجاد القدرة المطلوبة.
الحل
بتنفيذ الخطوات المقترحة نجد أن:
أو:
أو حوالي 78 حصان. (يجب عليك توفير الخطوات المستخدمة لتحويل الوحدات).
الدلالة
هذه كمية معقولة من القدرة ليوفرها محرك سيارة صغيرة إلى متوسطة الحجم (1حصان = 0.746كيلووات).
لاحظ أن هذه ليست سوى القدرة المستهلكة لتحريك السيارة. يذهب الكثير من قدرة المحرك إلى أماكن أخرى، على سبيل المثال، في الحرارة المهدرة. لهذا السبب تحتاج السيارات إلى مشعات radiators. يمكن استخدام أي قدرة متبقية للتسريع أو لتشغيل ملحقات السيارة.
المراجع
- موسوعة الفيزياء العامة، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، 2023.
- كتاب الفيزياء للجامعات، صموئيل جيه لينغ، جامعة ولاية ترومان، د. جيف ساني، جامعة لويولا ماريماونت ويليام مويبس.