التحليل العنقودي باستخدام الخوارزمية التصنيفية

التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis، هي أداة مصممة لتعيين الحالات إلى عدد ثابت K من المجموعات (المجموعات) التي لم تُعرف خصائصها بعد ولكنها تستند إلى مجموعة من المتغيرات المحددة. يكون مفيدًا للغاية عندما تريد تصنيف عدد كبير (آلاف) من الحالات.

التحليل العنقودي الجيد هو تحليل يتميز بكل من:

الكفاءة Efficient: يستخدم أقل عدد ممكن من المجموعات.
الفاعلية Effective: يلتقط جميع المجموعات المهمة إحصائيًا وتجاريًا. على سبيل المثال، قد تكون المجموعة التي تضم خمسة عملاء مختلفة إحصائيًا ولكنها ليست مربحة profitable جدًا.

مبادئ التحليل العنقودي باستخدام الخوارزمية التصنيفية

يبدأ إجراء التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means ببناء مراكز المجموعة الأولية. يمكنك تعيين هذه المراكز بنفسك أو جعل الإجراء يحدد عدد k من الملاحظات المتباعدة جيدًا well-spaced observations لمراكز المجموعة.

بعد الحصول على مراكز المجموعات الأولية، تقوم الخوارزمية بكل من:

تعيين الحالات إلى المجموعات بناءً على المسافة من مراكز المجموعة.
تحديث مواقع مراكز المجموعات بناءً على القيم المتوسطة mean values للحالات في كل مجموعة.

تتكرر هذه الخطوات حتى تؤدي أي إعادة تعيين للحالات إلى جعل المجموعات أكثر تنوعًا داخليًا أو متشابهة خارجيًا.

استخدام الخوارزمية التصنيفية K-Means لتصنيف العملاء

يريد مزود الاتصالات تقسيم قاعدة عملائه حسب أنماط استخدام الخدمة. إذا كان من الممكن تصنيف العملاء حسب الاستخدام، فيمكن للشركة تقديم حزم أكثر جاذبية لعملائها.

المتغيرات المعيارية التي تشير إلى استخدام الخدمة واردة في ملف telco_extra.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات. استخدم إجراء تحليل الكتلة K-Means للعثور على مجموعات فرعية من العملاء “المماثلين”.

تشغيل التحليل

لتشغيل التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis:

1. اختر من القوائم: تحليل> تصنيف> K-Means Cluster …

Analyze > Classify > K-Means Cluster…

يظهر مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis كما يلي:

2. إذا لم تعرض قائمة المتغيرات تسميات المتغيرات بحسب ترتيب الملفات، فانقر بزر الماوس الأيمن في أي مكان في قائمة المتغيرات ومن قائمة السياق context، اختر عرض تسميات المتغيرات Display Variable Labels والفرز حسب ترتيب الملفات Sort by File Order.

3. حدد المتغيرات من “قياسيًا المسافات الطويلة” Standardized log-long distance ولغاية “قياسيًا لاسلكي” Standardized log-wireless والمتغيرات “خطوط متعددة قياسيًا” Standardized multiple lines ولغاية “الفوترة الإلكترونية قياسيًا” Standardized electronic billing كمتغيرات تحليل analysis variables.

4. اكتب 3 كعدد المجموعات number of clusters.

5. انقر فوق تكرار Iterate.

يظهر مربع الحوار تكرار Iterate كما يلي:

مربع الحوار تكرار Iterate - التحليل العنقودي باستخدام الخوارزمية التصنيفية — مربع الحوار تكرار Iterate – التحليل العنقودي باستخدام الخوارزمية التصنيفية

6. اكتب 20 كأقصى عدد من التكرارات maximum iterations.

7. انقر فوق متابعة Continue.

8. انقر فوق خيارات Options في مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis.

يظهر مربع حوار الخيارات كما يلي:

مربع حوار الخيارات - التحليل العنقودي باستخدام الخوارزمية التصنيفية — مربع حوار الخيارات – التحليل العنقودي باستخدام الخوارزمية التصنيفية

9. حدد جدول أنوفا ANOVA table ومعلومات المجموعة لكل مجموعة Cluster information for each group في مجموعة الإحصائيات Statistics.

10. حدد استبعاد الحالات الزوجي Exclude cases pairwise في مجموعة القيم المفقودة Missing Values. هناك العديد من القيم المفقودة نظرًا لحقيقة أن معظم العملاء لا يشتركون في جميع الخدمات، لذا فإن استبعاد الحالات الزوجية يزيد من المعلومات التي يمكنك الحصول عليها من البيانات … على حساب احتمال انحياز النتائج.

11. انقر فوق “متابعة” Continue، ثم انقر فوق “موافق” OK في مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis.

مراكز المجموعات الأولية

الشكل التالي يبين مراكز المجموعة الأولية لحل ثلاثي المجموعات Initial cluster centers for three-cluster solution:

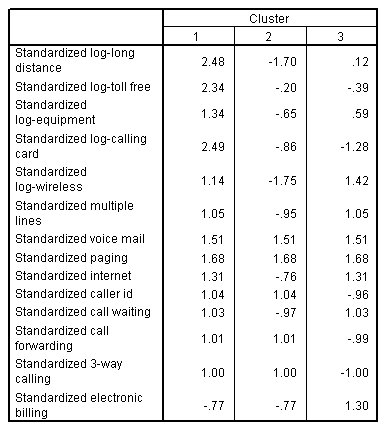
مراكز المجموعة الأولية هي قيم المتغيرات variable values للملاحظات المتباعدة جيدًا k well-spaced observations.

تاريخ التكرار

الشكل التالي يبين تاريخ التكرار لحل ثلاثي المجموعات Iteration history for three-cluster solution:

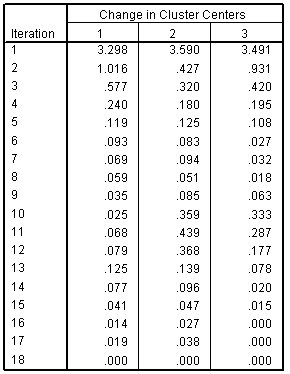
يُظهر تاريخ التكرار تقدم عملية التجميع في كل خطوة. في التكرارات المبكرة، تتحول مراكز المجموعات كثيرًا. بحلول التكرار الرابع عشر، استقروا في المنطقة العامة لموقعهم النهائي، والتكرارات الأربعة الأخيرة هي تعديلات طفيفة.

إذا توقفت الخوارزمية بسبب الوصول إلى الحد الأقصى لعدد التكرارات، فقد ترغب في زيادة الحد الأقصى لأن الحل قد يكون غير مستقر بخلاف ذلك. على سبيل المثال، إذا تركت الحد الأقصى لعدد التكرارات عند 10، فسيظل الحل المبلغ عنه في حالة تدفق.

جدول ANOVA

الشكل التالي يبين جدول تحليل التباين ANOVA لحل ثلاثي المجموعات:

يشير جدول ANOVA إلى المتغيرات الأكثر مساهمة في حل المجموعة الخاص بك. توفر المتغيرات ذات قيم F الكبيرة أكبر فصل بين المجموعات.

مراكز المجموعة النهائية

الشكل التالي يبين مراكز المجموعة النهائية Final cluster centers لحل ثلاثي المجموعات three-cluster solution:

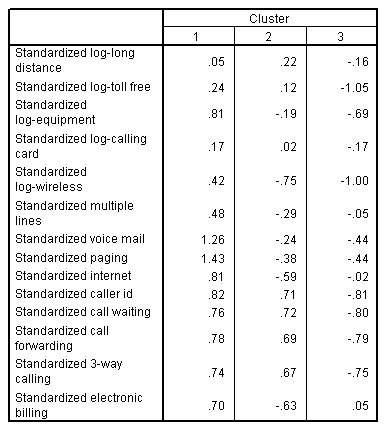
يتم حساب مراكز المجموعة النهائية على أنها المتوسط لكل متغير داخل كل مجموعة نهائية. تعكس مراكز المجموعة النهائية خصائص الحالة النموذجية لكل مجموعة أو عنقود cluster.

يميل العملاء في المجموعة 1 إلى أن يكونوا من كبار المنفقين الذين يشترون الكثير من الخدمات.
ويميل العملاء في المجموعة 2 إلى أن يكونوا منفقين معتدلين يشترون خدمات “الاتصال” calling.
كما يميل العملاء في المجموعة 3 إلى إنفاق القليل جدًا وعدم شراء العديد من الخدمات.

المسافات بين مراكز المجموعة النهائية

الشكل التالي يبين المسافات بين مراكز المجموعة النهائية Distances between final cluster centers لحل ثلاثي المجموعات three-cluster solution:

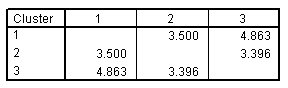
يوضح هذا الجدول المسافات الإقليدية بين مراكز المجموعة النهائية. مسافات أكبر بين المجموعات تتوافق مع اختلافات أكبر.

المجموعات 1 و 3 هي الأكثر اختلافًا.
تتشابه المجموعة 2 بشكل متساوٍ مع المجموعات 1 و 3.

يمكن أيضًا فهم هذه العلاقات بين المجموعات من مراكز المجموعات النهائية، ولكن هذا يصبح أكثر صعوبة مع زيادة عدد المجموعات والمتغيرات.

عدد الحالات في كل مجموعة

الشكل التالي يبين عدد الحالات في كل مجموعة لحل ثلاثي المجموعات:

تم تخصيص عدد كبير من الحالات للمجموعة الثالثة، والتي للأسف المجموعة الأقل ربحية. ربما يمكن استخراج كتلة رابعة أكثر ربحية من مجموعة “الخدمة الأساسية” basic service هذه.

استخدام الخوارزمية التصنيفية في بناء حل من أربع مجموعات

لتشغيل تحليل الخوارزمية التصنيفية بأربع مجموعات:

1. أعد فتح مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis.

يظهر مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis كما يلي:

مربع حوار التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis

2. اكتب 4 كعدد المجموعات number of clusters.

3. انقر فوق حفظ Save.

يظهر مربع الحوار حفظ Save dialog box كما يلي:

مربع الحوار حفظ - التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis — مربع الحوار حفظ – التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis

4. حدد عضوية المجموعة Cluster membership والمسافة من مركز المجموعة Distance from cluster center.

5. انقر فوق متابعة Continue.

6. انقر فوق “موافق” OK في مربع حوار الخوارزمية التصنيفية K-Means Cluster Analysis.

7. يمكن استخدام المتغيرات المحفوظة لإنشاء مخطط مربع boxplot مفيد. من القوائم، اختر: الرسوم البيانية> منشئ المخطط …

Graphs > Chart Builder…

8. انقر فوق علامة التبويب معرض Gallery، وحدد Boxplot من قائمة أنواع المخططات chart types، واسحب وأفلت أيقونة Simple Boxplot على اللوحة.

9. قم بسحب وإفلات “مسافة الحالة من مركز مجموعة التصنيف الخاص بها” Distance of Case from its Classification Cluster Center على المحور ص y axis.

10. قم بسحب وإسقاط “عدد حالات المجموعة” Cluster Number of Case على المحور س x axis.

11. انقر فوق “موافق” OK لإنشاء مخطط مربع boxplot.

يظهر منشئ الرسم البياني كما يلي:

منشئ المخططات - التحليل العنقودي باستخدام الخوارزمية التصنيفية — منشئ المخططات – التحليل العنقودي باستخدام الخوارزمية التصنيفية

مخطط المسافات من مركز المجموعة حسب عضوية المجموعة

الشكل التالي يبين رسم بياني للمسافات من مركز المجموعة حسب عضوية المجموعة لحل من أربع مجموعاتPlot of distances from cluster center by cluster membership for four-cluster solution:

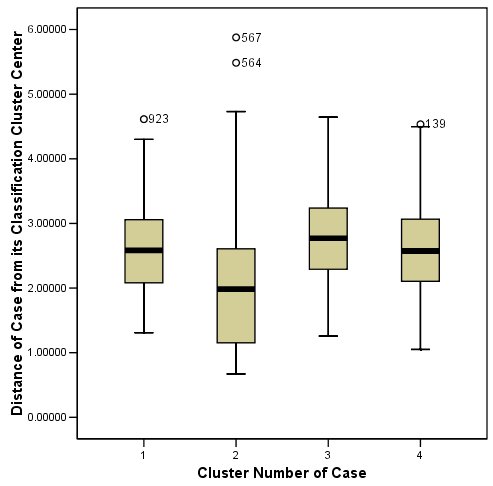
هذا مخطط تشخيصي يساعدك في العثور على القيم المتطرفة outliers داخل المجموعات. هناك الكثير من التباين في المجموعة 2، لكن جميع المسافات تقع في نطاق المعقول.

مراكز المجموعة النهائية

الشكل التالي يبين مراكز المجموعة النهائية Final cluster centers لحل من أربع مجموعات four-cluster solution:

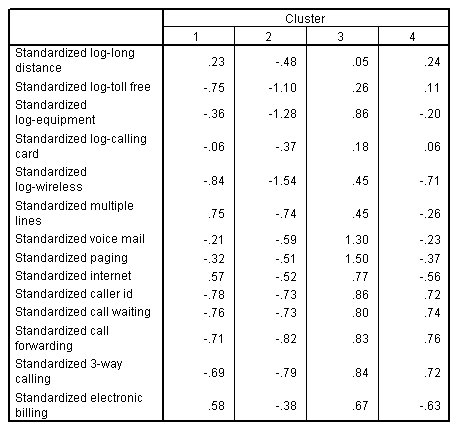
مراكز الكتلة النهائية لحل من أربع مجموعات - التحليل العنقودي باستخدام الخوارزمية التصنيفية — مراكز الكتلة النهائية لحل من أربع مجموعات – التحليل العنقودي باستخدام الخوارزمية التصنيفية

يوضح هذا الجدول عدم وجود مجموعة مهمة في حل المجموعات الثلاث. يتم اختيار أعضاء المجموعتين 1 و 2 إلى حد كبير من المجموعة 3 في الحل المكون من ثلاث مجموعات، ومن غير المرجح أن يكونوا من كبار المنفقين. ومع ذلك، من المرجح جدًا أن يشتري أعضاء المجموعة 1 خدمات مرتبطة بالإنترنت Internet-related services، مما يجعلها مجموعة متميزة وربما مربحة.

يبدو أن المجموعتين 3 و 4 تتوافقان مع المجموعتين 1 و 2 من الحل المكون من ثلاث مجموعات.

المسافات بين مراكز المجموعة النهائية

الشكل التالي يبين المسافات بين مراكز المجموعة النهائية لحل من أربع مجموعات Distances between final cluster centers for four-cluster solution:

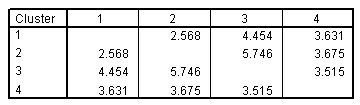
لم تتغير المسافات بين المجموعات بشكل كبير.

المجموعات 1 و 2 هي الأكثر تشابهًا، وهذا أمر منطقي لأنه تم دمجها في مجموعة واحدة في حل ثلاثي المجموعات.
تعتبر المجموعتان 2 و 3 هي الأكثر اختلافًا، حيث إنها تمثل سلوكيات إنفاق معاكسة.
لا تزال المجموعة 4 مماثلة للمجموعات الأخرى.

عدد الحالات في كل مجموعة

الشكل التالي يبين عدد الحالات في كل مجموعة لحل من أربع مجموعات:

ما يقرب من 25٪ من الحالات تنتمي إلى مجموعة عملاء “الخدمة الإلكترونية” E-service التي تم إنشاؤها حديثًا، وهو أمر مهم جدًا لأرباحك.

ملخص استخدام الخوارزمية التصنيفية K-Means Cluster Analysis

باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis، قمت في البداية بتجميع العملاء في ثلاث مجموعات. ومع ذلك، لم يكن هذا الحل مُرضيًا للغاية، لذلك أعدت إجراء التحليل بأربع مجموعات. كانت هذه النتائج أفضل، ومن مراكز المجموعات النهائية، رأيت أن مجموعة “الإنترنت” Internet التي يحتمل أن تكون مربحة قد فُقدت في الحل المكون من ثلاث مجموعات.

يؤكد هذا المثال على الطبيعة الاستكشافية للتحليل باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis، حيث إنه من المستحيل تحديد “أفضل” عدد من المجموعات حتى تقوم بتشغيل التحليلات وفحص الحلول.

الخطوة التالية للشركة هي محاولة بناء نموذج يصنف العملاء وفقًا لمعلوماتهم الديموغرافية. باستخدام هذا النموذج، يمكن للشركة تخصيص العروض للعملاء المحتملين الفرديين. للحصول على معلومات حول كيفية قيام الشركة ببناء مثل هذا النموذج، راجع موضوع استخدام التحليل التمييزي لتصنيف عملاء الاتصالات.

الإجراءات ذات الصلة

إجراء التحليل العنقودي باستخدام الخوارزمية التصنيفية K-Means Cluster Analysis هو أداة لإيجاد مجموعات طبيعية للحالات، بالنظر إلى قيمها على مجموعة من المتغيرات. يكون مفيدًا للغاية عندما تريد تصنيف عدد كبير (آلاف) من الحالات.

يسمح لك إجراء التحليل العنقودي من خطوتين TwoStep Cluster Analysis باستخدام كل من المتغيرات الفئوية والمتصلة، ويمكنك تلقائيًا تحديد “أفضل” عدد من المجموعات.
إذا كنت تريد تجميع المتغيرات بدلاً من الحالات، أو لديك عدد قليل من الحالات، فجرّب إجراء التحليل العنقودي الهرمي.
إذا كانت الخوارزمية التصنيفية K-Means Cluster Analysis الخاصة بك جزءًا من حل التجزئة، فيمكن تحليل هذه المجموعات المنشأة حديثًا في إجراء التحليل التمييزي.

المصدر

التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات
الموقع الرسمي لشركة IBM ® برنامج SPSS