استخدام تحليل العوامل لاكتشاف البنية
يرغب مزود الاتصالات في فهم أنماط استخدام الخدمة بشكل أفضل في قاعدة بيانات العملاء الخاصة به. إذا كان من الممكن تجميع الخدمات حسب الاستخدام، يمكن للشركة تقديم حزم وعروض أكثر جاذبية لعملائها. يمكن تنفيذ هذه الاستراتيجية من خلال استخدام تحليل العوامل أو التحليل العاملي Factor Analysis لاكتشاف البنية في قاعدة بيانات العملاء.
تم تضمين عينة عشوائية من قاعدة بيانات العملاء في ملف telco.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات. استخدم تحليل العوامل لتحديد البنية الأساسية في بيانات استخدام الخدمة.
تشغيل إجراء تحليل العوامل
1. لإجراء تحليل العوامل، اختر من القوائم: تحليل> اختصار الأبعاد> عاملي …
Analyze > Dimension Reduction > Factor…
يظهر مربع حوار تحليل العوامل Factor Analysis كما يلي:
2. إذا لم تعرض قائمة المتغيرات variable list تسميات المتغيرات بحسب ترتيب الملفات، فانقر بزر الماوس الأيمن في أي مكان في قائمة المتغيرات ومن قائمة السياق context، اختر عرض تسميات المتغيرات Display Variable Labels والفرز حسب ترتيب الملفات Sort by File Order.
3. حدد الحقول “المسافة الطويلة الشهر الماضي” Long distance last month ولغاية “اللاسلكي الشهر الماضي” Wireless last month والحقول من “خطوط متعددة” Multiple lines ولغاية “الفوترة الإلكترونية” Electronic billing كمتغيرات التحليل analysis variables.
4. انقر فوق الوصفي Descriptives.
يظهر مربع حوار الوصفي Descriptives كما يلي:
5. حدد Anti-image و KMO و Bartlett’s test of sphericity.
6. انقر فوق متابعة Continue.
7. انقر فوق استخراج Extraction في مربع حوار تحليل العوامل Factor Analysis.
يظهر مربع حوار الاستخراج Extraction كما يلي:
8. حدد تحليل المحور الرئيسي Principal axis factoring من قائمة الطريقة Method.
9. حدد مخطط خطي Scree plot.
10. انقر فوق متابعة Continue.
11. انقر فوق التدوير Rotation في مربع حوار تحليل العوامل Factor Analysis.
يظهر مربع حوار التدوير Rotation dialog كما يلي:
12. حدد Varimax في مجموعة الطريقة Method.
13. حدد تحميل مخطط (مخططات) Loading plot(s) في مجموعة العرض Display.
14. انقر فوق متابعة Continue.
15. انقر فوق “موافق” في مربع حوار تحليل العوامل Factor Analysis.
اختبار KMO واختبار Bartlett’s
الشكل التالي يبين نتائج اختبار KMO واختبار Bartlett’s:

يعرض هذا الجدول اختبارين يشيران إلى مدى ملاءمة بياناتك لاكتشاف البنية. مقياس Kaiser-Meyer-Olkin لكفاية أخذ العينات هو إحصاء يشير إلى نسبة التباين في متغيراتك التي قد تكون ناجمة عن عوامل أساسية. تشير القيم العالية (القريبة من 1.0) بشكل عام إلى أن تحليل العوامل قد يكون مفيدًا مع بياناتك. إذا كانت القيمة أقل من 0.50، فمن المحتمل ألا تكون نتائج التحليل العاملي مفيدة للغاية.
يختبر اختبار Bartlett للكروية الفرضية القائلة بأن مصفوفة الارتباط الخاصة بك هي مصفوفة هوية identity matrix، والتي من شأنها أن تشير إلى أن متغيراتك غير مرتبطة وبالتالي غير مناسبة لاكتشاف البنية. تشير القيم الصغيرة (أقل من 0.05) لمستوى الدلالة إلى أن تحليل العوامل قد يكون مفيدًا مع بياناتك.
المجتمعات Communalities
الشكل التالي يبين المجتمعات Communalities:
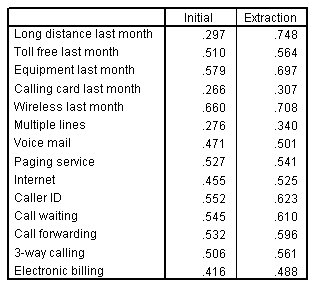
المجتمعات Communalities هي، لتحليلات الارتباط، نسبة التباين التي يتم حسابها في كل متغير بواسطة بقية المتغيرات.
مجتمعات الاستخراج Extraction communalities هي تقديرات للتباين في كل متغير يتم حسابه بواسطة العوامل في الحل العاملي. تشير القيم الصغيرة إلى متغيرات لا تتناسب بشكل جيد مع الحل العاملي، وربما ينبغي إسقاطها من التحليل. تعتبر عمليات الاستخراج المشتركة لهذا الحل مقبولة، على الرغم من أن القيم المنخفضة لحقل الخطوط المتعددة Multiple lines وبطاقة الاتصال Calling card تظهر أنها لا تتناسب مع الآخرين.
تفسير التباين الكلي في تحليل العوامل
الشكل التالي يبين تفسير التباين الكلي Total variance explained، القيم الذاتية الأولية eigenvalues:
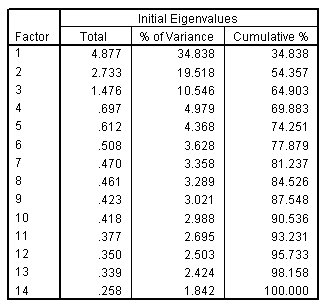
يوضح القسم الموجود في أقصى اليسار من هذا الجدول التباين المُفسر بواسطة الحل الأولي. ثلاثة عوامل فقط في الحل الأولي لها قيم ذاتية أكبر من 1. معًا، تمثل هذه العوامل ما يقرب من 65٪ من التباين في المتغيرات الأصلية. يشير هذا إلى أن هناك ثلاثة تأثيرات كامنة مرتبطة باستخدام الخدمة، ولكن لا يزال هناك مجال للكثير من الاختلافات غير المبررة.
الشكل التالي يبين تفسير التباين الكلي Total variance explained، العوامل المستخرجة extracted factors:
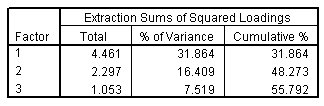
يوضح القسم الثاني من هذا الجدول التباين المُفسر بالعوامل المستخرجة قبل التدوير. التباين التراكمي cumulative variability الذي تفسره هذه العوامل الثلاثة في الحل المستخلص هو حوالي 55٪، بفارق 10٪ عن الحل الأولي. وبالتالي، يتم فقد حوالي 10٪ من التباين الذي يفسره الحل الأولي بسبب العوامل الكامنة الفريدة للمتغيرات والمتغيرات الأصلية التي لا يمكن تفسيرها ببساطة بواسطة النموذج العاملي.
الشكل التالي يبين تفسير التباين الكلي، العوامل المدورة Total variance explained, rotated factors:
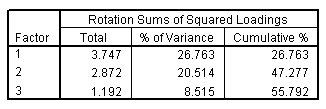
يوضح القسم الموجود في أقصى اليمين من هذا الجدول التباين المُفسر بالعوامل المستخرجة بعد التدوير. يقوم النموذج العاملي المدور بإجراء بعض التعديلات الصغيرة على العوامل 1 و 2، لكن العامل 3 يُترك دون تغيير تقريبًا. ابحث عن التغييرات بين مصفوفات العوامل غير المدورة والمدورة لترى كيف يؤثر الدوران على تفسير العامل الأول والثاني.
المخطط الخطي Scree Plot
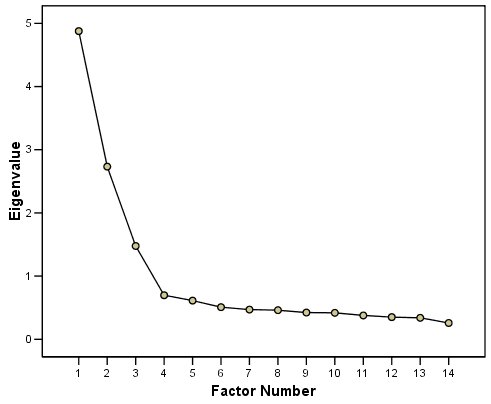
في الشكل أعلاه المخطط الخطي Scree Plot مع القيم الذاتية eigenvalues على المحور الرأسي والعوامل factors الموجودة على المحور الأفقي، وهو تُظهر منحدرًا حادًا للأسفل للعوامل الثلاثة الأولى
تؤكد المخطط الخطي Scree Plot اختيار ثلاثة مكونات.
مصفوفة العامل
الشكل التالي يبين مصفوفة العامل Factor matrix:
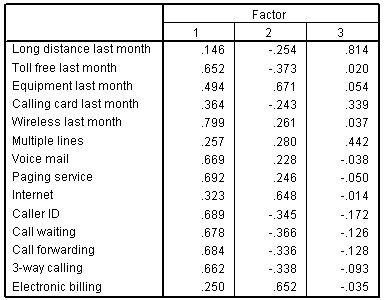
العلاقات في مصفوفة العوامل غير المدورة واضحة إلى حد ما. العامل الثالث مرتبط بحقل “المسافات الطويلة الشهر الماضي” Long distance last month. العامل الثاني يتوافق بشدة مع حقول “المعدات الشهر الماضي” Equipment last month والإنترنت Internet والفواتير الإلكترونية Electronic billing. يرتبط العامل الأول بحقول “الرقم المجاني الشهر الماضي” Toll free last month، و”اللاسلكي الشهر الماضي” Wireless last month، والبريد الصوتي Voice mail، وخدمة المناداة Paging service، ومعرف المتصل Caller ID، وانتظار المكالمات Call waiting، وإعادة توجيه المكالمات Call forwarding، والمكالمات ثلاثية الاتجاهات 3-way calling. ومع ذلك، فإن بعض خدمات “العامل الأول” هذه ترتبط سلبًا بالعامل الثاني؛ والبعض الآخر ترتبط بشكل إيجابي. بشكل عام، هناك الكثير من الخدمات التي لها ارتباطات أكبر من 0.2 مع عوامل متعددة، مما يفسد الصورة. يجب أن توضح مصفوفة العامل المدورة rotated factor matrix هذا الأمر.
مصفوفة العامل المدورة
الشكل التالي يبين مصفوفة تحويل العامل Factor transformation matrix:
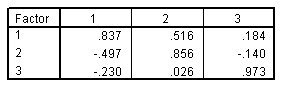
تصف مصفوفة تحويل العامل الدوران المحدد المطبق على الحل العاملي الخاص بك. تُستخدم هذه المصفوفة لحساب مصفوفة العامل المدورة من مصفوفة العامل الأصلية (غير المدورة). تتوافق العناصر الأصغر خارج القطر مع التدوير الأصغر Smaller off-diagonal elements correspond to smaller rotations. تتوافق العناصر الأكبر خارج القطر مع دوران أكبر Larger off-diagonal elements correspond to larger rotations.
الشكل التالي يبين مصفوفة العامل المدورة Rotated factor matrix:
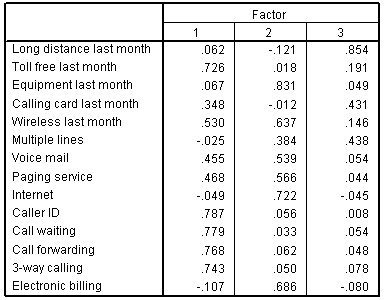
العامل الثالث لا يتأثر إلى حد كبير بالتدوير، ولكن من السهل تفسير العامل الأول والثاني الآن. يرتبط العامل الأول الذي تم تدويره ارتباطًا وثيقًا بالرقم المجاني الشهر الماضي Toll free last month، ومعرف المتصل Caller ID، وانتظار المكالمات Call waiting، وتحويل المكالمات Call forwarding، والمكالمات ثلاثية الاتجاهات 3-way calling. لا ترتبط هذه المتغيرات بشكل خاص بالعاملين الآخرين.
العامل الثاني هو الأكثر ارتباطًا بالمعدات الشهر الماضي Equipment last month والإنترنت Internet والفواتير الإلكترونية Electronic billing.
الخلاصة
وبالتالي، هناك ثلاث مجموعات رئيسية من الخدمات، كما تحددها الخدمات الأكثر ارتباطًا بالعوامل الثلاثة. بالنظر إلى هذه المجموعات، يمكنك إبداء الملاحظات التالية حول الخدمات المتبقية:
- نظرًا لارتباطاتها الكبيرة إلى حد ما مع كل من العاملين الأول والثاني، فإن الاتصال اللاسلكي الشهر الماضي Wireless last month والبريد الصوتي Voice mail وخدمة النداء Paging service تعمل على ربط مجموعتي “الإضافات” Extras و”التقنية” Tech.
- بطاقة الاتصال الشهر الماضي Calling card last month مرتبطة بشكل معتدل بالعاملين الأول والثالث، وبالتالي فهي تربط بين مجموعتي “الإضافات” Extras و”المسافات الطويلة” Long Distance.
- ترتبط الخطوط المتعددة Multiple lines بشكل معتدل بالعاملين الثاني والثالث، وبالتالي فهي تربط بين مجموعتي “التقنية” Tech و”المسافة الطويلة” Long Distance.
هذا يشير إلى سبل البيع العابر cross-selling. على سبيل المثال، قد يكون العملاء الذين يشتركون في خدمات إضافية extra services أكثر استعدادًا لقبول عروض خاصة على الخدمات اللاسلكية wireless services بدلاً من خدمات الإنترنت Internet services.
الشكل التالي يبين مخطط ثلاثي الأبعاد لتحميل العوامل Factor loadings plot:
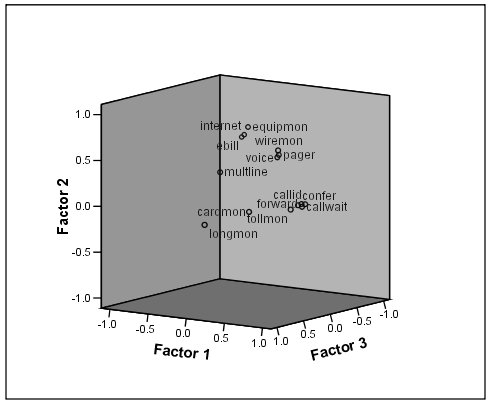
مخطط تحميل العامل هو تمثيل مرئي لمصفوفة العامل المدورة rotated factor matrix. إذا كانت العلاقات في المصفوفة معقدة، فقد يكون تفسير هذا المخطط أسهل.
ملخص استخدام تحليل العوامل لاكتشاف البنية
باستخدام استخراج عوامل المحور الرئيسي، لقد كشفت عن ثلاثة عوامل كامنة تصف العلاقات بين المتغيرات الخاصة بك. تشير هذه العوامل إلى أنماط مختلفة لاستخدام الخدمة، والتي يمكنك استخدامها لزيادة المبيعات المتقاطعة بكفاءة أكبر.
الإجراءات ذات الصلة
يحاول تحليل العوامل Factor Analysis تحديد المتغيرات الأساسية التي تشرح نمط الارتباطات ضمن مجموعة من المتغيرات الملاحظة. غالبًا ما يستخدم هذا الإجراء لتقليل عدد المتغيرات في مجموعة بيانات ولكن يمكن أيضًا استخدامه لاستكشاف البنية الكامنة للمتغيرات في ملف البيانات الخاص بك.
إذا كنت تعتقد أن العلاقات بين المتغيرات الخاصة بك غير خطية nonlinear، فإن إجراء تحليل الارتباطات ثنائية المتغير يقدم معاملات ارتباط أكثر ملاءمة للارتباطات غير الخطية.
إذا لم تكن متغيرات التحليل الخاصة بك متغيرات من نوع المقياس scale، يمكنك تجربة التحليل العنقودي الهرمي على المتغيرات كبديل لتحليل العوامل لاكتشاف البنية.
المصدر
- التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات
- الموقع الرسمي لشركة IBM ® برنامج SPSS