اختبار ت لعينتين مرتبطتين Paired-Samples T Test
يستخدم إجراء اختبار ت لعينتين مرتبطتين Paired-Samples T Test لاختبار فرضية عدم وجود فرق بين متغيرين. قد تتكون البيانات من قياسين تم إجراؤهما على نفس الموضوع أو قياس واحد مأخوذ من زوج متطابق من الموضوعات.
أحد أكثر التصاميم التجريبية شيوعًا هو التصميم “قبل اللاحق”. غالبًا ما تتكون دراسة من هذا النوع من قياسين يتم إجراؤهما على نفس الموضوع، أحدهما قبل إدخال العلاج أو المنبه والآخر بعده. والفكرة الأساسية هي بسيطة. إذا لم يكن للعلاج أي تأثير، فإن متوسط الفرق بين القياسات يساوي 0 وتثبت الفرضية الصفرية. من ناحية أخرى، إذا كان للعلاج تأثير (مقصود أو غير مقصود!)، فإن متوسط الفرق ليس 0 ويتم رفض فرضية العدم أو الفرضية الصفرية.
بالإضافة إلى ذلك، ينتج عن هذا الإجراء:
- الإحصاء الوصفي لكل متغير اختبار
- علاقة ارتباط بيرسون بين كل زوج وأهميته
- فترة ثقة لمتوسط الفرق (95٪ أو قيمة تحددها)
مثال تطبيقي على اختبار ت لعينتين مرتبطتين
هل النظام الغذائي يحدث فرقًا؟
تقوم طبيبة بتقييم نظام غذائي جديد لمرضاها الذين لديهم تاريخ عائلي من أمراض القلب. لاختبار فعالية هذا النظام الغذائي، يتم وضع 16 مريضًا على النظام الغذائي لمدة 6 أشهر. يتم قياس أوزانهم ومستويات الدهون الثلاثية قبل الدراسة وبعدها، وتريد الطبيبة معرفة ما إذا كانت أي مجموعة من القياسات قد تغيرت.
يستخدم هذا المثال الملف dietstudy.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات. استخدم اختبار ت لعينتين مرتبطتين Paired-Samples T Test لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين أوزان ما قبل وما بعد النظام الغذائي ومستويات الدهون الثلاثية لهؤلاء المرضى.
إجراء التحليل
لبدء تحليل اختبار ت لعينتين مرتبطتين:
1. اختر من القوائم: تحليل> مقارنة المتوسطات> اختبار ت للعينات المرتبطة …
Analyze > Compare Means > Paired-Samples T Test…
يظهر مربع حوار اختبار ت للعينات المرتبطة Paired-Samples T Test كما يلي:
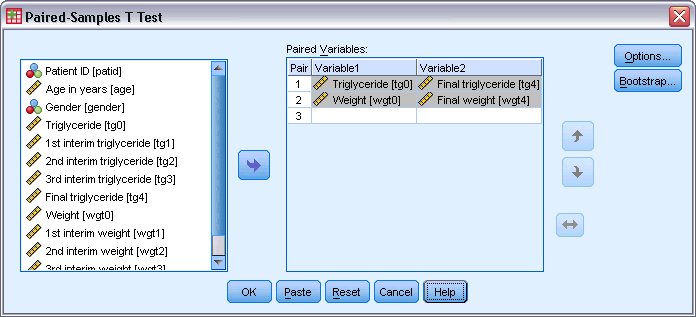
2. حدد Triglyceride و Final Triglyceride كأول مجموعة من المتغيرات المرتبطة.
3. حدد الوزن Weight والوزن النهائي Final Weight كمجموعة ثانية من المتغيرات المرتبطة.
4. انقر فوق “موافق” OK.
الإحصاء الوصفي
يعرض جدول الإحصاء الوصفي المتوسط وحجم العينة والانحراف المعياري والخطأ المعياري لكلا المجموعتين.
- في جميع المواد الـ 16، انخفضت مستويات الدهون الثلاثية بين 14 و 15 نقطة في المتوسط بعد 6 أشهر من النظام الغذائي الجديد.
- من الواضح أن الأشخاص قد فقدوا الوزن خلال فترة الدراسة؛ في المتوسط، حوالي 8 باوندات.
- تكشف الانحرافات المعيارية لقياسات ما قبل وما بعد النظام الغذائي أن الأشخاص كانوا أكثر تباينًا فيما يتعلق بالوزن مقارنة بمستويات الدهون الثلاثية.
ارتباطات بيرسون
عند قيمة -0.286، فإن العلاقة بين خط الأساس ومستويات الدهون الثلاثية لمدة ستة أشهر ليست ذات دلالة إحصائية. كانت المستويات أقل بشكل عام، لكن التغيير كان غير متسق عبر الحالات. خفض العديد من مستوياتهم، لكن العديد من الآخرين إما لم يغيروا أو زادوا من مستوياتهم.
من ناحية أخرى، فإن ارتباط بيرسون بين خط الأساس وقياسات الوزن لمدة ستة أشهر هو 0.996، وهو ارتباط مثالي تقريبًا. على عكس مستويات الدهون الثلاثية، فقد جميع الأشخاص الوزن وفعلوا ذلك باستمرار.
نتائج جدول اختبار ت لعينتين مرتبطين
الشكل التالي يبين نتائج جدول اختبار ت للعينات المرتبطة:
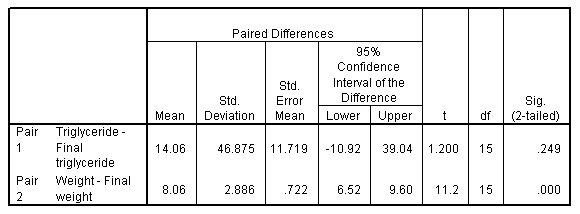
- يعرض عمود المتوسط Mean في جدول اختبار ت للعينات المقترنة متوسط الفرق بين قياسات الدهون الثلاثية والوزن قبل النظام الغذائي وستة أشهر خلال النظام الغذائي.
- يعرض عمود الانحراف المعياري Std. Deviation الانحراف المعياري لمتوسط فرق الدرجات.
- يوفر عمود متوسط الخطأ المعياري Std. Error Mean مؤشرًا للتباين الذي يمكن للمرء أن يتوقعه في عينات عشوائية متكررة من 16 مريضًا مشابهًا لتلك الموجودة في هذه الدراسة.
- توفر فترة الثقة 95٪ للاختلاف تقديرًا للحدود التي يقع بينها متوسط الاختلاف الحقيقي في 95٪ من جميع العينات العشوائية الممكنة لـ 16 مريضًا مشابهين لتلك المشاركة في هذه الدراسة.
- يتم الحصول على إحصاء ت t بقسمة متوسط الفرق mean difference على الخطأ المعياري standard error.
- يعرض العمود Sig. (2-tailed) احتمال الحصول على إحصاء ت t الذي تكون قيمته المطلقة مساوية أو أكبر من إحصاء ت t الذي تم الحصول عليه.
نظرًا لأن قيمة الأهمية للتغير في الوزن أقل من 0.05، يمكنك أن تستنتج أن متوسط الخسارة البالغ 8.06 رطل لكل مريض لا يرجع إلى الاختلاف بالصدفة، ويمكن أن يُعزى إلى النظام الغذائي. ومع ذلك، فإن قيمة الأهمية الأكبر من 0.10 للتغير في مستوى الدهون الثلاثية تظهر أن النظام الغذائي لم يقلل بشكل كبير من مستويات الدهون الثلاثية.
الإجراءات ذات الصلة
يكون اختبار ت للعينات المقترنة مناسبًا عندما يتم مقارنة متوسطات العينات ذات الصلة. من المفترض أن تتبع درجات الفرق توزيعًا طبيعيًا بشكل معقول، خاصة فيما يتعلق بالانحراف. قبل إجراء اختبار ت، يمكنك تقييم توزيع درجات الاختلاف عن طريق فحص الرسم البياني لمتغير الفرق المحسوب. يجب التحقق بعناية من متغيرات الاختبار ذات القيم المتطرفة أو البعيدة؛ يمكن استخدام إجراء boxplots لهذا الغرض.
إذا قمت بحساب الفرق بين المتغيرات المرتبطة، يمكنك بدلاً من ذلك استخدام إجراء اختبار ت لعينة واحدة.
المصدر
- كتاب التحليل الإحصائي باستخدام برنامج SPSS، ترجمة وإعداد: د. م. مصطفى عبيد، مركز البحوث والدراسات متعدد التخصصات، إسطنبول، تركيا، 2022.
- الموقع الرسمي لشركة IBM ® برنامج SPSS